3518
Unsupervised Deep Unrolled Reconstruction Powered by Regularization by Denoising1Biomedical Engineering, State University of New York at Buffalo, Buffalo, NY, United States, 2Electrical Engineering, State University of New York at Buffalo, Buffalo, NY, United States, 3Program of Advanced Musculoskeletal Imaging (PAMI), Cleveland Clinic, Cleveland, OH, United States, 4Paul C. Lauterbur Research Center for Biomedical Imaging, SIAT, CAS, Shenzhen, China
Synopsis
In this abstract, we propose a novel reconstruction method, named DURED-Net, that enables interpretable unsupervised learning for MR image reconstruction by combining an unsupervised denoising network and a plug-and-play method. Specifically, we incorporate the physics model into the denoising network using Regularization by Denoising (RED), and unroll the underlying optimization into a deep neural network. In addition, a sampling pattern was specially designed to facilitate unsupervised learning. Experiment results based on the knee fastMRI dataset exhibit marked improvements over the existing unsupervised reconstruction methods.
Introduction
Many studies have successfully applied deep learning in MR reconstruction1-6. However, a large amount of ground truth data are needed for training a robust reconstruction network, which may be impractical for some MRI applications. In this work, we propose a novel unsupervised method for MRI reconstruction by integrating an unsupervised CNN denoiser (Noise2Noise)7 and Regularization by Denoising (RED)8, which incorporates the physics model into the denoising network. In addition, the alternating direction method of multipliers (ADMM)9 iteration for RED is unrolled to a deep network whose parameters are learned from the unlabeled training data. In particular, our DURED-Net not only leverages the unsupervised capability of Noise2Noise by designing a special sampling pattern but also unrolls the ADMM-based iterations to a network such that the parameters of both networks are trained jointly. As a result, the proposed method avoids overfitting in the existing unsupervised methods.Method
In our unsupervised learning, the network learns the relationship between an aliased image (input) $$$\hat{x}_{1}^{i}$$$ and another aliased image (target) $$$\hat{x}_{2}^{i}$$$ using a large number of aliased images as the training data. Both aliased images are zero-filled reconstructions of the same image but different undersampling patterns. The network is trained by minimizing the loss function as follows $$\arg\min_{\theta}\frac{1}{n}\sum_{i=1}^{n}\left\| f \left(\hat{x}_{1}^{i},\theta\right)-\hat{x}_{2}^{i} \right\|^{2} \tag{1} $$Where $$$f\left( \cdot \right)$$$ is the neural network with the learned parameter $$$\theta$$$. It was demonstrated in Noise2Noise that such training is equivalent to training with the ground truth images as long as the conditioned expectation $$$\mathbb{E}\left\{ \hat{x}_{2}^{i}|\hat{x}_{1}^{i} \right\}$$$ is the ground truth image, and the aliasing artifacts in $$$\hat{x}_{1}^{i}$$$ and $$$\hat{x}_{2}^{i}$$$ are of the same distribution. To meet the conditions for unsupervised learning, we designed a random undersampling pattern whose probability density function (PDF) is $$$p\left( k \right)=e^{\left( {\frac{-1}{\mu}\left| k \right|} \right)^{\alpha}} \tag{2}$$$
where k is the k-space location, $$$\mu$$$ and $$$\alpha$$$ the parameters to control the sampling location. The sampled values are further weighted by $$$\frac{1}{p\left( k \right)}$$$. We can show the average of a large number of such aliased images gives the ground-truth image.
The network was designed based on the general compressed sensing reconstruction model $$\hat{x}=\arg\min_{x}\frac{1}{2}\left\| Ax-y \right\|^2+\lambda\rho\left( x \right) \tag{3}$$
where x is the latent image from its undersampled measurement y, and A is a measurement matrix that contains the undersampling process and Fourier transform. Using RED to incorporate a denoiser $$$f\left( \cdot \right)$$$, Eq. (3) becomes $$\hat{x}=\arg\min_{x}\frac{1}{2}\left\| Ax-y \right\|^2+\frac{1}{2}\lambda x^{T}\big( x-f\left(x\right)\big) \tag{4}$$
Using ADMM as the solver, Eq. (4) can be iteratively solved. The n-th iteration is updated as follows: $$\left\{ \begin{array}{lr}\textbf X^{\textbf n}: x^{n}=\left( A^{H}A+\beta I \right)^{-1} \left( A^{H}\left( y \right)+\beta\left( v^{n-1}-u^{n-1} \right) \right) , & \\\textbf Z^{\textbf n}:z^{n} = Z_{w}\left( v^{n-1} \right) , & \\\textbf V^{\textbf n}:v^{n} = -\frac{\lambda}{\beta}\left( z^{n} \right)+\left( x^{n}+u^{n-1} \right) , & \\\textbf U^{\textbf n}:u^{n} = u^{n-1} +\left( x^{n}-v^{n} \right) , & \\ \end{array}\tag{5}\right.$$
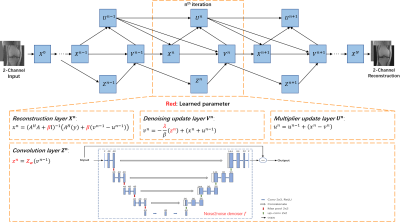
We unrolled Eq. (5) into a network, named DURED-net. Figure 1 illustrates the architecture of DURED-net when three iterations are unrolled to one training epoch. The four steps in Eq. (5) are represented as four layers in the neural network including the reconstruction layer $$$\textbf X^{\textbf n}$$$, the convolution layer $$$\textbf Z^{\textbf n}$$$, the denoising update layer $$$\textbf V^{\textbf n}$$$, and the multiplier update layer $$$\textbf U^{\textbf n}$$$. The n-th iteration corresponds to the n-th module of the deep network enclosed with the dashed box.
Results
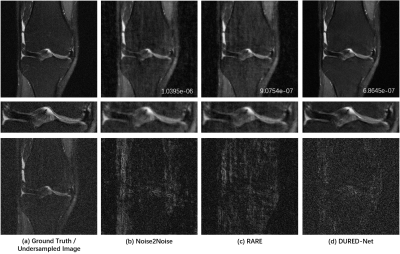
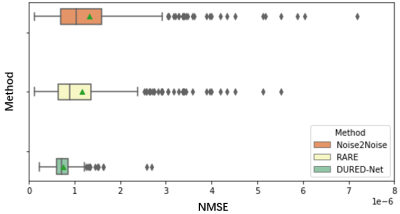
We used the raw single-coil k-space from the knee fastMRI dataset10-11 that is available publicly at https://fastmri.org/. In particular, we randomly selected 200 sagittal knee MR scans subjects and used them in the training procedure. There are out of the total 40 images for each subject, and we selected 20 central images that had the anatomy, which gave a total of 1000 images for training. We further selected another 20 different subjects in knee fastMRI dataset and picked up 20 central images for each subject, which gave additional 400 images for testing. The dataset with the Turbo Spin Echo sequence has parameters that are with the image size of 320×320, the echo train length of 4, the in-plane resolution of 0.5mm2, the slice thickness of 3mm, the TR time is 2200~3000 ms and TE time is 27 ~ 34 ms. All images are complex-valued.Figure 2 shows the reconstructions from 5x undersampled data using three different unsupervised networks, Noise2Noise, the state-of-the-art RARE12 network which adds physical models to a pre-trained Noise2Noise network, and our proposed DURED-Net. All training and testing images were generated using the undersampling patterns defined by Eq. (2). Figure 3 shows the boxplots of the normalized mean squared errors (NMSEs) of reconstructions for 400 testing images. It is seen that the reconstructions of the proposed method agree with the ground truth image well in terms of NMSE.
Conclusion
In this abstract, we proposed DURED-Net, a novel unsupervised deep reconstruction method for undersampled k-space data. Results demonstrate the superior performance of the proposed method over the state-of-the-art methods.Acknowledgements
No acknowledgement found.References
1. S. Wang, Z. Su, L. Ying, X. Peng, S. Zhu, F. Liang, D. Feng and D. Liang, "Accelerating magnetic resonance imaging via deep learning," 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI), 2016, pp. 514-517.
2. B. Zhu, J. Z. Liu, S. F. Cauley, B. R. Rosen, M. S. Rosen, "Image reconstruction by domain-transform manifold learning," Nature, vol. 555, pp. 487–492, 2018.
3. Y. Yang, J. Sun, H. Li, and Z. Xu, "ADMM-CSNet: A Deep Learning Approach for Image Compressive Sensing," in IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 42, no. 3, pp. 521-538, 2020.
4. K. Hammernik, T. Klatzer, E. Kobler, M. P. Recht, D. K. Sodickson, T. Pock and F. Knoll. "Learning a variational network for reconstruction of accelerated MRI data," Magn. Reson. Med., vol. 79, no. 2, pp. 3055-3071, 2018.
5. J. Zhang and B. Ghanem, "ISTA-Net: Interpretable Optimization-Inspired Deep Network for Image Compressive Sensing," 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018, pp. 1828-1837.
6. H. K. Aggarwal, M. P. Mani and M. Jacob, "MoDL: Model-Based Deep Learning Architecture for Inverse Problems," in IEEE Transactions on Medical Imaging, vol. 38, no. 2, pp. 394-405, 2019.
7. J. Lehtinen, J. Munkberg, J. Hasselgren, S. Laine, T. Karras, M. Aittala and T. Aila, "Noise2Noise: Learning Image Restoration without Clean Data," in Proceedings of the 35th International Conference on Machine Learning, 2018, pp. 2965-2974.
8. Y. Romano, M. Elad, and P. Milanfar, "The little engine that could: Regularization by denoising (RED)," SIAM J. Imag. Sci., vol. 10, no. 4, pp. 1804–1844, 2017.
9. S. Boyd, N. Parikh, E. Chu, B. Peleato and J. Eckstein, "Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers," Found. Trends Mach. Learn., 2011, pp. 1-122.
10. J. Zbontar, F. Knoll, A. Sriram, T. Murrell, Z. Huang, M. J. Muckley, ... and Y. W. Lui, "fastMRI: An Open Dataset and Benchmarks for Accelerated MRI," arXiv preprint arXiv:1811.08839, 2018.
11. F. Knoll, J. Zbontar, A. Sriram, M. J. Muckley, M. Bruno, A. Defazio, ... and Y. W. Lui, "fastMRI: A Publicly Available Raw k-Space and DICOM Dataset of Knee Images for Accelerated MR Image Reconstruction Using Machine Learning," Radiology: Artificial Intelligence, vol. 2, no. 1, e190007, 2020.
12. J. Liu, Y. Sun, C. Eldeniz, W. Gan, H. An and U. S. Kamilov, "RARE: Image Reconstruction Using Deep Priors Learned Without Groundtruth," in IEEE Journal of Selected Topics in Signal Processing, vol. 14, no. 6, pp. 1088-1099, 2020.
Figures