Introduction

Longitudinal MRI holds great potential for tracking in-vivo dynamics, such as aging, disease progression and cognitive change [1,2,3]. Based on the underlying similarity between longitudinal scans, we propose Delta Scan, a model-based and explainable framework that uses the previous MRI exams to accelerate future scans.

Methods

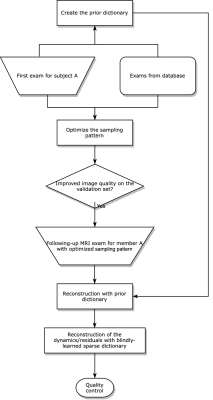
The basic assumptions of modeling longitudinal imaging include: (1) exams from the same participant have similar energy distribution (in k-space), and (2) structural changes between exams should be sparse under a certain transform. For (1), the sampling pattern is optimized based on the spectrum of the first exam. For (2), we design a model-based reconstruction algorithm to exploit prior information.The sampling pattern optimization workflow uses a Pareto optimization paradigm [4]. We propose to use stochastic gradient-based optimization when extending to the non-Cartesian case. The underlying assumption is that the energy distribution for the same subject should be similar across time. For signal reconstruction, we model image to be estimated as a combination of two components: 1) historical static information (i.e., the majority of the tissue structure remains the same), which we formulate as a block-matching process; 2) dynamic information (i.e., accounting for possible structural changes in tissue level and/or positional changes due to subject motion), which we model as a dictionary learning problem. The two sources of information are incorporated as the following two-stage optimization problem.

The cost function of the first stage is
$$\boldsymbol{x}_{1}=\underset{\boldsymbol{x}}{\arg \min } \min _{i_{j} \in\{1,2 \ldots N\}}\|\boldsymbol{A} \boldsymbol{x}-\boldsymbol{y}\|_{2}^{2}+\nu \sum_{j=1}^{N_{1}}\left\|\mathcal{P}_{j} \boldsymbol{x}-\boldsymbol{D}_{1}^{i_{j}}\right\|_{2}^{2},$$
where $$$\boldsymbol{A} $$$ is the MRI forward model and $$$\mathcal{P}$$$ is a collection of patch operators that decompose the image into local patches, with $$$N_{1}$$$ patches in total. The first term is usually called ‘data consistency.’ The second term involves block-matching operations inspired by the BM3D [5] method. To make the block-matching process more robust, the algorithm subtracts the phase and normalizes the atoms. The optimization alternates between the minimization of the data-consistency term (solved by the conjugate gradient method) and the block-matching operation.
With the first step's solution ($$$\boldsymbol{x}_{1}$$$), we formulate the the second stage as $$\boldsymbol{x}_{2}=\left\{\underset{\boldsymbol{x}}{\arg \min } \min _{\boldsymbol{D}_{2}, \boldsymbol{Z}_{2}}\left\|\boldsymbol{A}\left(\boldsymbol{x}+\boldsymbol{x}_{1}\right)-\boldsymbol{y}\right\|_{2}^{2}+\lambda_{1}\left\|\mathcal{P} \boldsymbol{x}-\boldsymbol{D}_{2} \boldsymbol{Z}_{2}\right\|_{2}^{2}+\lambda_{2}^{2}\left\|\boldsymbol{Z}_{2}\right\|_{0}\right\}+\boldsymbol{x}_{1}.$$The second stage assumes that the changes between exams should be sparse w.r.t. a certain transform. Instead of using fixed operations, such as the wavelet transform or the DCT, we learn a sparsifying dictionary $$$\boldsymbol{D}_{2}$$$ and its sparse code $$$\boldsymbol{Z}_{2}$$$ adaptively [6].

Experiments

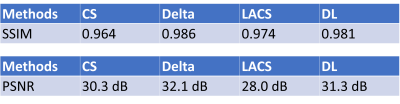
We compared the Delta reconstruction with previous reference-based MRI methods, namely LACS [7], which puts a weighted point-wise similarity constraint between MRI exams. We also compare with referenceless methods, including l1-Wavelets CS [8] and blind dictionary learning (DL) [6]. The dictionary learning method can be regarded as the second stage with $$$\boldsymbol{x}_{1}$$$ being zero.
The cohort consists of 8 subjects. Each of them received two consecutive exams with at least a six months gap on a 1.5T GE scanner. Local IRB gave approval. Each exam acquired a 3D MPRAGE sequence with FOVs between 24-26cm and matrix sizes of 192*192*170. The first scan has a 1D 2.5x undersampling in the phase encoding direction, and the second scan is fully-sampled.
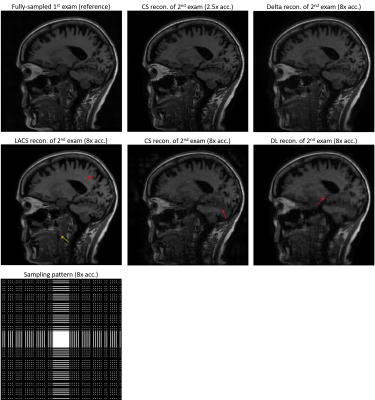
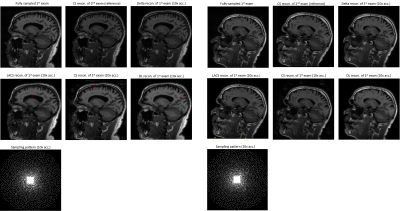
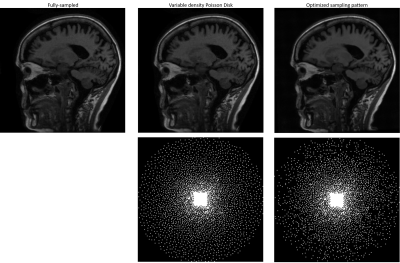
We compared several experiment settings: (1) The second exam is further retrospectively undersampled, with an undersampling ratio $$$\approx$$$8x. For reference-based methods, we use the conjugate phase reconstruction of the first fully-sampled exam as the prior. Fig. 2 shows the results. (2) The first exam is retrospectively undersampled following a 10x Poisson-disk sampling pattern. For reference-based methods, we used the CS-based reconstruction of the 2.5x undersampled second exam as the (high-quality) prior. Fig. 3 shows the results. (3) Joint sampling pattern optimization and delta reconstruction. Fig. 4 showcases the results.

Results

Fig. 2-4 exhibit examples of reconstructed images in different scenarios. In comparison with referenceless (CS or DL) reconstruction, Delta Reconstruction improves the image quality, with the high-quality reference scans as prior. More importantly, it could still capture subtle anatomical changes (yellow arrows) which do not exist in the reference exam. Fig. 3 shows that even if the reference exam is undersampled, the Delta reconstruction can still enhance the following exams. Compared to LACS, the method is more robust and avoids overfitting on the first exam. Though the cost function is not convex, the convergence is very pretty fast, usually within 5-6 iterations when $$$\nu$$$ is small. We guess that the regularizer could provide useful gradient information, and a small $$$\nu$$$ does not corrupt the convexity severely.

Conclusion

Delta Scan provides a fast, explainable, and robust method for longitudinal MRI, where the longitudinal MR exams are substantially accelerated with the structural information from the past scans. In the future we will conduct a more comprehensive radiological study, and extend Delta Scan to non-Cartesian and multi-contrast imaging.

Acknowledgements

No acknowledgement found.