3497

High-quality Lung imaging with FLORET UTE and Fibonacci interleaved trajectory ordering

Guruprasad Krishnamoorthy¹, Matthew M Willmering², Jason C Woods^2,3, and James G Pipe⁴
¹MR R&D, Philips Healthcare, Rochester, MN, United States, ²Center for Pulmonary Imaging Research, Divisions of Pulmonary Medicine and Radiology, Cincinnati Children’s Hospital Medical Center, Cincinnati, OH, United States, ³Departments of Pediatrics, Radiology, and Physics, University of Cincinnati College of Medicine, Cincinnati, OH, United States, ⁴Department of Radiology, Mayo Clinic, Rochester, MN, United States

Synopsis

FLORET (Fermat looped, orthogonally encoded trajectories) is an efficient center-out 3D spiral trajectory, and it supports ultra-short echo times. In this work, a new trajectory ordering scheme and FLORET balanced steady-state free precession (FLORET-bSSFP) were developed at 1.5T with inline reconstruction. Simulations, phantom, and human lung imaging were performed to compare the performance of the proposed trajectory ordering with standard ordering. The proposed trajectory ordering scheme minimized artifacts caused by the changing gradient moments while improving temporal stability and motion robustness. High-quality free-breathing lung images were obtained using FLORET-bSFFP and spoiled gradient echo-based UTE FLORET.

Introduction

FLORET (Fermat looped, orthogonally encoded trajectories) is an efficient center-out 3D spiral trajectory¹ and it supports ultra-short echo times². It is based on a single Fermat spiral waveform which is relatively easier to design when compared to a stack-of-cones³ trajectory requiring the design of multiple waveforms. FLORET spoiled gradient echo-based UTE sequence (FLORET-SPGR) has been shown to have applications in sodium imaging of the brain⁴ and knee^2,5, morphological⁶, and functional⁷ imaging of the lungs. This work developed a new trajectory ordering scheme and FLORET balanced steady-state free precession (FLORET-bSSFP). Eddy current effects and motion robustness of the proposed trajectory ordering and the conventional trajectory ordering¹ was compared with both FLORET-bSSFP and FLORET-SPGR sequences. The proposed method was fully implemented in the scanner platform for inline reconstruction of images.

Methods

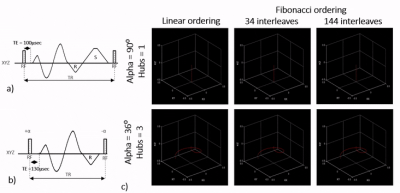
In the FLORET sequence as proposed by Pipe et al.¹., a single Fermat spiral waveform is rotated on the fly in a spherical coordinate system to cover 3D k-space based on the following equations, $$α(h, n) = α0*[1 - (2*n) / (N-1)]$$ $$β(h, n) = π*(3-√5)*n$$ where, $$$h = 0, 1, ...H-1$$$ hubs, $$$n = 0,1,..N-1$$$ arms to satisfy Nyquist criteria within each hub, α is the polar angle, β is the azimuthal angle, and α₀ is the polar coverage within a hub. The distribution of each spiral arm within a hub follows sunflower head pattern⁸ due to the golden angle $$$(π*(3-√5)≈137.5°)$$$ used. K-space can be critically sampled with a single hub with α₀of 90⁰ , two orthogonal hubs with α₀ ≥ 45⁰, or three orthogonal hubs with α₀ ≥ 36⁰ within each hub. The trajectory ordering, as mentioned above, will be called linear ordering henceforth.
The proposed trajectory ordering makes use of the inherent property of the golden angle similar to^9,10 and formulates an interleaved ordering as follows, $$α(i, h, f) = α0*[1 - (2*(i+f*i)) / (N-1)]$$ $$β(i,h,f) = π*(3-√5)*(i+f*i)$$ where, $$$i = 0, 1, 2,... I-1$$$ Fibonacci number of interleaves, $$$f={0,1,2...F-1,if iseven(i), F-1,F-2,…0,otherwise}$$$, f is FLORET arms per interleave. I and F and are chosen such that $$$I*F≈N$$$. The data acquisition is performed by first looping through f followed by h and then finally i. The proposed trajectory ordering will be called Fibonacci ordering hereafter in this article. The base Fermat spiral arm was generated with a modified version of the numerical solution described in ¹¹. Figure 1 shows the pulse sequence diagrams and animations of different trajectory schemes used in this work. The angular distance between the successive FLORET arms was calculated through simulations assuming that the angular distance is proportional to the changing gradient moments caused by the trajectory ordering scheme. These changing gradient moments can cause long-term eddy currents and can lead to image artifacts. The proposed method was fully implemented with inline reconstruction on a 1.5T Ambition-X system (Philips, Best, The Netherlands). Phantom images were acquired with FLORET-SPGR and FLORET-bSSFP sequences. Free-breathing volunteer lung imaging was performed based on a study approved by the local institutional review board with written informed consent. The data acquisition was limited to the end-expiratory state using a motion-sensing camera (VitalEye^TM, Philips, Best, The Netherlands) with a gating efficiency of 60%. A combination of 16-channel anterior and 12-channel posterior phased array coils was used for signal reception. The sequence parameters used for the volunteer scan are outlined in Table 1. The signal-to-noise (SNR) ratio of the lung parenchyma was estimated on images by dividing the mean signal measured in lung parenchyma and standard deviation measured in a large blood vessel.

Results and Discussions

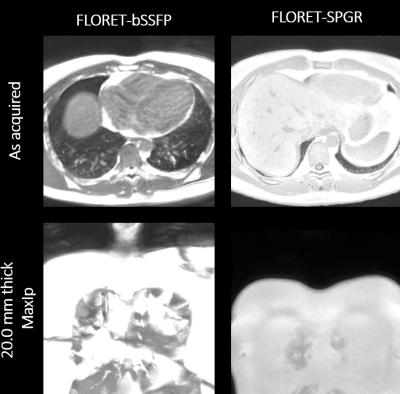
As shown in Figure 1b, Fibonacci ordering samples k-space more uniformly than the linear ordering at any given time interval. This ordering may be more suitable for applying advanced reconstruction techniques like KWIC¹² for dynamic imaging applications. Fibonacci ordering with all configurations had a substantially smaller angular distance than linear ordering, shown in Figure 2a. Fibonacci ordering with the 1 Hub configuration generally had a smaller angular distance than the 3 Hub configurations due to the acquisition of orthogonal hubs in successive interleaves with the 3 Hub configuration. Images acquired with linear ordering showed visible artifacts in both sequences. In contrast, the Fibonacci ordering had no noticeable artifact even in a highly interleaved configuration, shown in phantom scans in Figure 2b. The differences are likely due to the long-term eddy currents caused by the changing gradient moments for the different ordering schemes. Free-breathing lung images acquired with FLORET-bSSFP are shown in Figure 3. Fibonacci ordering showed minimal B0 artifacts compared to the linear ordering and increased robustness to motion artifacts (bulk, cardiac and, residual respiratory motion) with an increased number of interleaves. Representative lung images acquired with FLORET-bSSFP and FLORET-SPGR sequences using the proposed arm ordering scheme are shown in Figure 4. The SNR of lung parenchyma obtained with FLORET-SPGR was 11.6, while the SNR obtained with FLORET-bSSFP was 2.9. This difference in SNR may be due to the scan time difference between the sequences, and we believe FLORET-bSSFP can significantly benefit from further scan parameter optimization.

Conclusion

The proposed trajectory ordering for FLORET minimizes eddy current artifacts in both SPGR and bSSFP sequences while improving temporal stability and robustness to motion artifacts.

Acknowledgements

No acknowledgement found.

References

1. Pipe JG, Zwart NR, Aboussouan EA, Robison RK, Devaraj A, Johnson KO. A new design and rationale for 3D orthogonally oversampled k-space trajectories. Magn Reson Med. 2011;66(5):1303-1311. doi:https://doi.org/10.1002/mrm.22918

2. Robison RK, Anderson III AG, Pipe JG. Three-dimensional ultrashort echo-time imaging using a FLORET trajectory. Magn Reson Med. 2017;78(3):1038-1049. doi:https://doi.org/10.1002/mrm.26500

3. Gurney PT, Hargreaves BA, Nishimura DG. Design and analysis of a practical 3D cones trajectory. Magn Reson Med. 2006;55(3):575-582. doi:https://doi.org/10.1002/mrm.20796

4. Madelin G, Kline R, Walvick R, Regatte RR. A method for estimating intracellular sodium concentration and extracellular volume fraction in brain in vivo using sodium magnetic resonance imaging. Sci Rep. 2014;4(1):4763. doi:10.1038/srep04763

5. Brown R, Lakshmanan K, Madelin G, et al. A flexible nested sodium and proton coil array with wideband matching for knee cartilage MRI at 3T. Magn Reson Med. 2016;76(4):1325-1334. doi:https://doi.org/10.1002/mrm.26017

6. Willmering MM, Robison RK, Wang H, Pipe JG, Woods JC. Implementation of the FLORET UTE sequence for lung imaging. Magn Reson Med. 2019;82(3):1091-1100. doi:https://doi.org/10.1002/mrm.27800

7. Willmering MM, Niedbalski PJ, Wang H, et al. Improved pulmonary 129Xe ventilation imaging via 3D-spiral UTE MRI. Magn Reson Med. 2020;84(1):312-320. doi:https://doi.org/10.1002/mrm.28114

8. H V. A better way to construct the sunﬂower head. Math Biosci. 1979;44:179-189.

9. Piccini D, Littmann A, Nielles-Vallespin S, Zenge MO. Spiral phyllotaxis: The natural way to construct a 3D radial trajectory in MRI. Magn Reson Med. 2011;66(4):1049-1056. doi:10.1002/mrm.22898

10. Krishnamoorthy G, Smink J, Tourais J, Breeuwer M, Kouwenhoven M. Variable anisotropic FOV for 3D radial imaging with spiral phyllotaxis (VASP). Magn Reson Med. 2021;85(1):68-77. doi:10.1002/mrm.28449

11. Pipe JG, Borup DD. Generating spiral gradient waveforms with a compact frequency spectrum. Magn Reson Med. n/a(n/a). doi:https://doi.org/10.1002/mrm.28993

12. Song HK, Dougherty L. k-Space weighted image contrast (KWIC) for contrast manipulation in projection reconstruction MRI. Magn Reson Med. 2000;44(6):825-832. doi:https://doi.org/10.1002/1522-2594(200012)44:6<825::AID-MRM2>3.0.CO;2-D

Figures

Figure 1: Pulse sequence diagram of a) FLORET-SPGR and b) the newly developed FLORET-bSSFP used in this work. S = Spoiler, R = Rewinder, RF = hard rectangular excitation pulse. C) Animations showing different trajectory ordering filling k-space through time.

Figure 2: a) Angular distance between successive sequence repetitions as an estimation of changing gradient moments for different trajectory ordering schemes used in this study. B) Phantom images acquired with different sequences and trajectory ordering schemes. Images acquired with linear arm ordering had artifacts likely due to the eddy currents caused by the larger change in gradient moments. No such artifacts were observed in Fibonacci ordering even in a highly interleaved configuration.

Table 1: Pulse sequence parameters used for volunteer lung imaging.

Figure 3: Images acquired with FLORET-bSSFP using different ordering schemes. Images with linear ordering had visible artifacts likely caused by eddy currents (yellow arrow). These artifacts were not visible in Fibonacci ordering even in a highly interleaved setup. Fibonacci ordering with larger number of interleaves showed improved robustness to motion with better vessel conspicuity (green arrow). Also, visibly less motion artifacts were observed in the images of Fibonacci ordering acquired with more interleaves compared to the images with lesser interleaves (blue arrow).

Figure 4: Representative lung images acquired with FLORET-bSSFP sequence and FLORET-SPGR sequences using highly interleaved Fibonacci arm ordering. FLORET-bSSFP was acquired in 610 interleaves with 55 FLORET arms per interleave while the FLORET-SPGR was acquired in 987 interleaves with 49 FLORET arms per interleave in 3 hubs.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

3497

DOI: https://doi.org/10.58530/2022/3497