Introduction

There has been much recent interest in deep learning for MRI reconstruction that combines additional information or priors into the network structure such as data consistency. Incorporating additional priors into deep learning could enable the learned models to generalize better [4]. This work examines optimized parallel combinations of deep networks and conventional regularized reconstruction for improved quality of MR image reconstructions from undersampled measurements. We observe that combining the image features from multiple approaches in a parallel fashion with appropriate weights leads to more effective representations that outperform strictly supervised or (unsupervised) conventional iterative methods. We repeat the parallel combinations similar to an unrolled network, where conventional (e.g., sparsity-based) features complement deep network learned features in every layer to provide effective reconstruction.

Proposed Reconstruction Approach

Model-based regularized reconstruction problems have been widely used in MRI, where we solve for an image:
$$ \hat{x}=\underset{x}{\arg\min} ~\sum_{c=1}^{N_c}\|A_cx - y_c \|^{2}_2 + \gamma \mathcal{R}(x)$$
where $$$y_c \in \mathbb{C}^p, \ c=1, \ldots, N_c$$$ represent acquired k-space measurements from $$$ N_c$$$ coils. The forward operator for the $$$c^{th}$$$ coil is denoted by $$$A_c = M \mathcal{F} S_c$$$, where $$$M \in \{0,1\}^{p\times q}$$$ is a masking operator that describes the pattern for sampling data in k-space, $$$\mathcal{F}\in \mathbb{C}^{q\times q}$$$ is the Fourier transform operator, and $$$S_c \in \mathbb{C}^{q\times q}$$$ is the $$$c^{th}$$$ coil-sensitivity matrix.
In compressed-sensing based MR Image reconstruction methods (CSMRI)[1,2], the regularizer is chosen to be $$$\mathcal{R}(x) = \| W x\|_{1}$$$ where $$$W$$$ is a sparsifying transform operator. As MR images are known to be sparse in the wavelet domain [2], we chose $$$W$$$ in our case to be the wavelet operator. So, for the (unsupervised) regularized reconstruction problem, we solve an optimization problem of the form:
$$ \underset{x}{\arg\min} \sum_{c=1}^{N_c} \|A_c x - y_c\|_2^2 + \gamma \| W x\|_{1}$$

Suppose we have an initial estimate of the underlying image such as the aliased input image $$$x^0$$$. Let $$$B^{i}(.)$$$ denote the function representing the $$$i^{th}$$$ iteration of an iterative algorithm and $$$x^{i+1}$$$ be the reconstructed image at the end of the iteration then, $$$x^{i+1} = B^{i}(x^{i})$$$. Applying $$$K$$$ iterations of the algorithm, we have,
$$x_{unsup} = \mathcal{S}_{\text{CSMRI}}(x^0;K) = B^{K}\circ B^{K-1} \circ ... B^{0}(x^0)$$
where $$$\circ$$$ represents function composition. We use the subscript ``unsup" for unsupervised as this reconstruction does not use paired training data. Similarly model-based supervised (unrolled) deep learning schemes such as MODL [3], use regularizers of the form :
$$\mathcal{R}_{sup}(x) = \|x- D_{\theta}(\bar{x})\|_2^2$$
within their architecture, where $$$D_{\theta}(.)$$$ is the CNN based denoiser, and $$$\bar{x}$$$ is it's input. Now, if $$$\mathcal{S}_{\theta}^{l}(.)$$$ denotes the $$$i^{th}$$$ iteration of a deep unrolled algortihm (MODL), then we have :

$$\mathcal{S}_{\theta}^{l}(x^l) = \mathcal{S}\big(x^l,\gamma, \{A_c,y_c\}_{c=1}^{N_c} \big) \\ =\underset{x}{\arg\min}~ \sum_{c=1}^{N_c} \|A_c x - y_c\|_2^2 +\beta \|x-\big(D_{\theta}(x^l))\|_2^2$$.
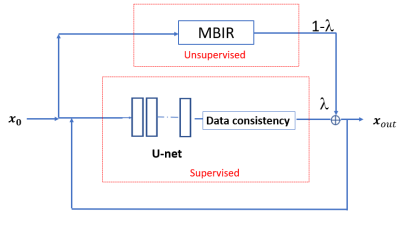
We propose combining the (unsupervised) conventional regularized method and the deep network based supervised method (MODL) in a parallel complimentary manner as follows with weights $$$\lambda$$$ and $$$(1-\lambda)$$$ respectively ($$$0 \leq \lambda \leq 1$$$):
$$\mathcal{P}^{l}_{\theta,\lambda}(x^l) = x^{l+1} = \lambda \mathcal{S}_{\theta}^{l}(x^l) + (1-\lambda) \mathcal{S}_{\text{CSMRI}}(x^0;K)$$
So, in the $$$l^{th}$$$ iteration of the parallel implementation, the deep network reconstruction output at the $$$l^{th}$$$ iteration is linearly combined with the appropriate weights with the unsupervised reconstruction output. So, after $$$L$$$ iterations of the parallel implementation, the output is defined by $$$x_{\text{out}}$$$

$$ x_{\text{out}} = x^L = \mathcal{P}_{\theta,\lambda}^{L-1} \circ \mathcal{P}_{\theta,\lambda}^{L-2} \circ ... \mathcal{P}_{\theta,\lambda}^{0}(x^0) = \mathcal{M}_{\theta,\lambda}(x^0,L) $$

Algorithms for training

We use the Projected Gradient Descent (PGD) algorithm to solve the unsupervised reconstruction problem with wavelet domain sparsity and $$$\gamma=0.0005$$$. We use pairwise training data (from the multi-coil knee dataset with $$$N_c=15$$$ coils in the fastMRI dataset) to train the deep network in the proposed architecture (Fig. 1). The training loss function was:
$$\hat{\theta},\hat{\lambda} = \arg\min_{\theta,\lambda} \sum_{i}^{N} \big (\big \|x^{\text{true}}_{\text{i}} - \mathcal{M}_{\theta,\lambda}(x_i^{0},L) \big\|_2^2)$$
where the $$$i^{th}$$$ training pair consists of the aliased image and the ground-truth image ($$$x_i^{0},x^{\text{true}}_{\text{i}}$$$). We used the ADAM optimizer [6] to minimize the cost function in the above equation, and $$$\theta$$$ and $$$\lambda$$$ were both updated for each batch with different learning rates. The U-Net architecture was used for the network ($$$\theta$$$) with a batchsize of 2 during training and the conjugate gradient descent algorithm was used in the data consistency module in the supervised learned block in Fig. 1. Our observation was that if the network was initialized with random weights, then $$$\lambda$$$ converged quickly to 0 giving more importance to the CSMRI output. So, a network was first pre-trained in Fig. 1 with a fixed value (initial estimate) of $$$\lambda$$$ (we used $$$\lambda = 0.5 $$$ in experiments) and then the network and $$$\lambda$$$ were then both updated from this initial state to further optimize them jointly.

Results and Conclusion

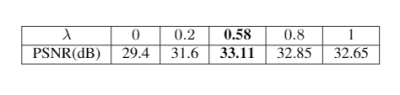
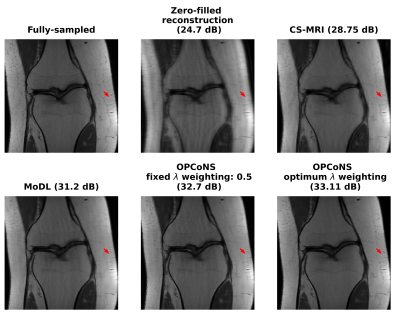
From the average reconstruction PSNR results in Figure 2, we observe that the OPCoNS reconstruction method (with $$$L=6$$$ iterations) outperforms strictly supervised learning (MoDL [3]) as well as (unsupervised) sparsity-based reconstruction (CS-MRI [2]) on the 15 tested multi-coil knee scans from the FastMRI Dataset [5]. Jointly adapting the weight $$$\lambda$$$ and the network parameters enables learning richer features that are otherwise missed by the strictly supervised or conventional iterative methods. This suggests complementarity between the supervised deep learning and unsupervised or iterative methods of reconstruction and hence combining them in a parallel fashion is a viable approach for improving MR reconstruction performance.

Acknowledgements

The work was supported by a research gift from the Advanced Radiology Services (ARS) foundation.