3484
Model-based PSF-encoded multi-shot EPI reconstruction with low-rank constraints1Mayo Clinic Graduate School of Biomedical Sciences, Rochester, MN, United States, 2Department of Radiology, Mayo Clinic, Rochester, MN, United States
Synopsis
Echo planar imaging (EPI) is commonly used clinically for its speed, but is sensitive to non-idealities including system field inhomogeneity and subject-specific susceptibility effects. Multi-shot techniques encoding an auxiliary point-spread-function (PSF)-encoding dimension provide robustness to off-resonance effects, with demonstrated potential for diffusion and anatomic applications, but incur scan time penalties motivating acquisition and reconstruction strategies to increase acceleration. This work proposes a comprehensive model-based iterative reconstruction framework for anatomic PSF-encoded EPI scans incorporating low-rank constraints, directly reconstructing undistorted images from undersampled data. Advantages are demonstrated using brain MRI data acquired on a compact 3T MRI system.
Overview
Echo planar imaging (EPI)1 is commonly used clinically for its speed, but is sensitive to system field inhomogeneity2 and subject-specific magnetic susceptibility.3 Off-resonance is typically neglected in image reconstruction, resulting in geometric distortion along the phase-encoding dimension and signal dropout in regions of susceptibility variation. Multi-shot techniques encoding an auxiliary point-spread-function (PSF) dimension overcome these limitations,4–6 showing potential in diffusion and anatomic applications.7,8 However, multi-shot encoding increases scan time, motivating acquisition and reconstruction techniques to push acceleration. PSF-EPI anatomic scans may also exhibit residual flow-induced ghosting artifacts.8 This work proposes a model-based iterative reconstruction (MBIR) framework with low-rank constraints for anatomic PSF-encoded EPI scans. Circumventing modular unfolding operations on intermediary datasets, we reconstruct undistorted images directly from undersampled data. Images generated with MBIR have reduced residual ghosting and improved signal recovery in regions of susceptibility, demonstrated with brain MRI data acquired on a compact 3T system.9Methods
Signal Model & Image ReconstructionThe PSF-encoded EPI signal measured during readout $$$u\in [0,U)$$$ of phase-encoding line $$$v\in [0,V)$$$ within an auxiliary pass $$$p \in [0,P)$$$ has triple Fourier encoding respectively in $$$k_x$$$, $$$k_y$$$, and $$$k_a$$$. The discretized10 signal can be modeled as
$$
\mathbf{G}[u,v,p,c]
=
\sum_{i=0}^{M-1}
\sum_{l=0}^{N-1}
s_c[i,l]
f[i,l]
e^{-\jmath \Delta \omega [i,l] \tau[v]}
e^{-\jmath (k_x[u] x[i] + k_y[v] y[l] + k_a[p] y[l])}
+
\mathbf{\epsilon}[u,v,p,c]
\tag{1}
$$
where we neglect T2* decay, assume row-flipping and pre-correction of eddy current and gradient delays,11,12 presume linear gradients,13 and model off-resonance effects manifesting only along the phase-encoding dimension during high-bandwidth EPI readouts.14 Here, $$$f$$$ is the target signal in pixel indices $$$i\in[0,M)$$$ and $$$l\in[0,N)$$$, $$$\Delta \omega$$$ is the B0 field map, $$$s_c$$$ is the sensitivity profile for coil $$$c\in [0,C)$$$, $$$\tau[v]=vT$$$ for echo spacing $$$T$$$, and $$$\mathbf{\epsilon}$$$ is Gaussian noise.
Without access to a field map, we target a composite unknown $$$\mathbf{\Theta}[i,l,q]\overset{\Delta}{=} \rho[i,l] e^{-\jmath \Delta \omega[i,l] \gamma_q T}$$$, i.e., the product of magnetization and the off-resonance field, where $$$\rho(x,y) \equiv f(x,y) e^{-\jmath \Delta \omega(x,y)t_0}$$$ for time $$$t_0$$$ between RF isodelay and initial readout. We partition the measurement window into $$$Q$$$ time segments,15 each with $$$q$$$th segment center $$$\gamma_q$$$, assuming constant temporal field inhomogeneity evolution in each segment,16 enabling FFTs and implicitly presuming low-rank properties. This yields a 3-way tensor with third unfolding $$$\mathbf{\Theta}_{[3]} = \sum_{i,l,q} \delta_{i+lM} \mathbf{\Theta}[i,l,q] \delta_q^T$$$, where $$$\delta$$$ is Kronecker's delta; scaled by a time-bandpass filter $$$\mathbf{\Phi}_q$$$ segmenting the acquisition window into $$$Q$$$ time segments and $$$Q+1$$$ breakpoints:
$$
\mathbf{G}[u,v,p,c]
=
\sum_{q=0}^{Q}
\mathbf{\Phi}_q[v]
\sum_{i=0}^{M-1}
\sum_{l=0}^{N-1}
s_c[i,l]
\rho[i,l]
e^{-\jmath \Delta \omega [i,l]\gamma_q T}
e^{-\jmath (k_x[u] x[i] + k_y[v] y[l] + k_a[p] y[l])}
+
\mathbf{\epsilon}[u,v,p,c]
\tag{2}
$$
This abstracts to
$$
\mathbf{G}_{[3]}
=
\sum_{q=0}^{Q}
\sum_{c=0}^{C-1}
\big(
\delta_c \otimes \mathbf{\Lambda}_q\text{diag}(\mathbf{S}_{[3]} \delta_c )
\big)
\mathbf{\Theta}
\mathbf{\Phi}
+
\mathbf{\epsilon},
\tag{3}
$$
where $$$\mathbf{S}_{[3]}$$$ is the $$$MN\times C$$$ unfolding of sensitivity maps, with Kronecker's product $$$\otimes$$$ and triple Fourier encoding operator
$$
\mathbf{\Lambda}_q
\overset{\Delta}{=}
(\mathbf{\Xi}_\text{a} \mathbf{F}_\text{a} \otimes I)
\big( \text{diag} (\mathbf{\Xi}_\text{p} \mathbf{F}_\text{p})^T \otimes I \big)
(I \otimes \mathbf{F}_{\text{ro}})
\tag{4}
$$
$$$\mathbf{F}_\text{a}$$$, $$$\mathbf{F}_\text{p}$$$, and $$$\mathbf{F}_{\text{ro}}$$$ respectively denote auxiliary, phase-encoding, and readout Fourier encoding; and $$$\mathbf{\Xi}$$$ are undersampling operators. The target $$$\mathbf{\Theta}$$$ can be estimated with least-squares optimization:
$$
\hat{\mathbf{\Theta}}
=
\underset{\mathbf{\Theta}}{\text{arg min}}
\bigg\{
\Omega(\mathbf{\Theta})\overset{\Delta}{=}
\bigg\lVert
\sum_{q=0}^{Q}
\sum_{c=0}^{C-1}
\big( \delta_c \otimes \mathbf{\Lambda}_q \text{diag} (\mathbf{S}_{[3]} \delta_c) \big)
\mathbf{\Theta}
\mathbf{\Phi}
-
\mathbf{G}_{[3]}
\bigg\rVert_F^2
\bigg\}
\tag{5}
$$
where $$$\lVert \cdot \rVert_F$$$ is the Frobenius norm. We solve (5) with conjugate gradient iteration.
Data Acquisition & Processing
Under an IRB-approved protocol, a healthy volunteer was scanned on a compact 3T MRI system.9 T2-weighted, PSF-encoded EPI (T2-DIADEM)7,8 was completed according to Table 1, with in-plane acceleration factor 3 and reduced PSF encodings for a reduced field of view (rFOV) factor of 8. Preceding MBIR or standard reconstruction, row flipping, ramp sampling, and phase correction in k-space were completed, and sensitivity profiles estimated using vendor-provided tools. In a standard reconstruction, PSF-encoded images were unfolded in the phase-encoding dimension using SENSE;17,18 then resulting data were unfolded in the PSF-encoding dimension before calculating distortion-free and distorted images.6 Instead, MBIR was completed with $$$Q=20$$$ time segments and 10 conjugate gradient iterations. Reconstruction and processing were completed in Matlab (The MathWorks, Inc., Natick, MA, USA). Post-processing included zero-padding, Fermi window apodization, intensity correction, and image-domain gradient nonlinearity correction.
Results
Images reconstructed with MBIR showed reduced ghosting artifact and modest advantages in recovering signal in regions of susceptibility. Figures 1 and 2 show comparisons between standard images and images generated with MBIR. Ghosting artifact is seen anterior to the basilar artery and near the optic nerve in standard images, but is reduced for MBIR. Figure 3 illustrates signal recovery from a region near the sinuses with line profiles, with increased recovery for MBIR compared to standard and sharper transition between air and anatomical signal.Discussion & Conclusion
Images reconstructed with the proposed framework have reduced ghosting and improved signal recovery in regions adjacent to susceptibility. These preliminary findings suggest MBIR may enhance the capabilities of T2-weighted anatomic imaging with PSF-encoded EPI. With improved image quality at fixed acquisition time and reconstruction directly from undersampled data, MBIR could enable further acceleration, a key limitation to broad adoption of PSF-EPI techniques. Future work will encompass regularization to explore further potential for artifact suppression and signal recovery, and adaptation for diffusion applications.Acknowledgements
This work is supported by National Institutes of Health (NIH) U01 EB024450, NIH U01 EB026979, Mayo Clinic Graduate School of Biomedical Sciences, and the National Science Foundation (NSF) Graduate Research Fellowship Program (GRFP).References
1. Mansfield P. J Phys C Solid State Phys. 1977;10(3):L55.
2. Jezzard P, Balaban RS. Magn Reson Med. 1995;34(1):65–73.
3. Cordes D, Turski PA, Sorenson JA. Magn Reson Imaging. 2000;18(9):1055–68.
4. Robson MD, Gore JC, Constable RT. Magn Reson Med. 1997;38(5):733–40.
5. Zaitsev M, Hennig J, Speck O. Magn Reson Med. 2004;52(5):1156–66.
6. In MH, Posnansky O, Speck O. Neuroimage;148:20–30.
7. In MH, Tan ET, Trzasko JD, et al. J Magn Reson Imaging. 2020;51(1):296–310.
8. In MH, Campeau NG, Huston III J, et al. Proc Intl Soc Mag Reson Med. 2021;0838.
9. Foo TK, Laskaris E, Vermilyea M, et al. Magn Reson Med. 2018;80(5):2232–45.
10. Fessler J. IEEE Signal Process Mag. 2010; 81–9.
11. Ahn CB, Cho ZH. IEEE Trans Med Imaging. 1991;10(1):47–52.
12. Tao S, Weavers PT, Trzasko JD, et al. Magn Reson Med. 2017;77(6):2250–62.
13. Tao S, Trzasko JD, Gunter JL, et al. Phys Med Biol. 2017;62(2):N18–31.
14. Yarach U, Bernstein MA, Huston III J, et al. Proc Intl Soc Mag Reson Med. 2019;0929.
15. Sutton BP, Noll DC, Fessler JA. IEEE Trans Med Imaging. 2003;22(2):178–88.
16. Balachandrasekaran A, Mani M, Mathews JM. IEEE Trans Med Imaging 2019;38(4):979-990.
17. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. Magn Reson Med. 1999;42(5):952–62.
18. King KF, Angelos L. Proc Intl Soc Mag Reson Med. 2001;1771.
Figures

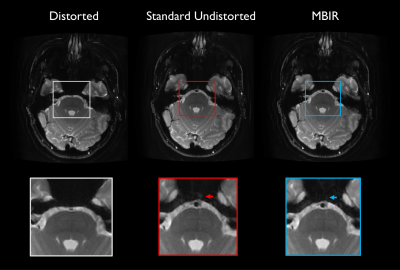
Fig. 1 Comparison of images generated with standard processing versus proposed reconstruction. Images and insets are identically windowed. Ghosting artifact anterior to the basilar artery is seen for the standard undistorted image (red arrow) but reduced in MBIR.
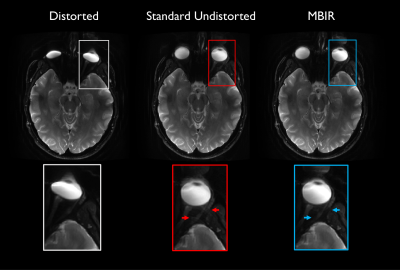
Fig. 2 Additional images generated with standard processing versus proposed reconstruction in slices containing the eyes. Images are identically windowed. Distortion of the globe and ghosting artifact adjacent to the optic nerve seen in standard undistorted image (red arrows) are diminished by MBIR.
