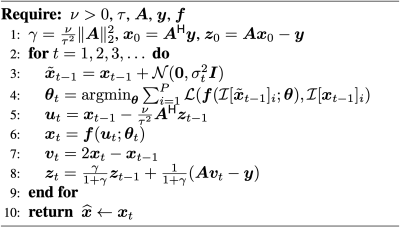Introduction

The data acquisition process in magnetic resonance imaging (MRI) is inherently slow. More recently, deep learning (DL)-based reconstruction methods have been shown to generate high-quality images from highly undersampled data. Typically, these methods rely on supervised learning and thus require a large corpus of training data. Compared to DL methods that train end-to-end networks, plug-and-play (PnP) methods iteratively solve an inverse problem by calling a denoiser within each iteration [1]. When a generic denoiser, e.g., BM3D [2], is used, PnP methods do not require training data. However, it has been recently demonstrated that the performance of PnP can be improved by employing an application-specific denoiser, typically trained using DL [3]. These denoisers do not require fully sampled k-space data but instead can be trained on images or image patches. However, these high-quality images or image patches may still not be available for some MRI applications, especially dynamic applications. More recently, there has been an increased interest in developing self-supervised methods that require no training data at all [4, 5]. In this work, we propose and validate a self-supervised method, called recovery with a self-calibrated denoiser (ReSiDe), for MRI reconstruction that requires no training data.

Methods

Traditional compressed sensing methods to recover image $$$\boldsymbol{x}\in\mathbb{C}^N$$$ from multi-coil noisy measurements $$$\boldsymbol{y}\in\mathbb{C}^M$$$ solve the following optimization problem:
$$\hat{\boldsymbol{x}}= argmin_\boldsymbol{x} \{\frac{1}{2\tau^2}\|\boldsymbol{Ax}-\boldsymbol{y}\|_2^2+\phi(\boldsymbol{x})\}\dots (1)$$
where $$$\boldsymbol{A}\in\mathbb{C}^{M×N}$$$ is a known forward operator, $$$\tau^2$$$ represents the variance of the measurement noise, and $$$\phi(\boldsymbol{x})$$$ is a sparsity-promoting regularizer. Many iterative algorithms can solve Eq. 1, including the alternating directions method of multipliers (ADMM) and primal-dual splitting (PDS) [6]. PnP methods simply replace a “proximal” operator in ADMM or PDS with a call to a denoiser. Training an application-specific denoiser, $$$\boldsymbol{f}(\cdot)$$$, relies on supervised learning, which requires access to clean images; such images may not be available for many applications. In response, we propose a PnP-inspired method that iteratively trains the denoiser from the image being recovered. The resulting method, called ReSiDe, is implemented using a modified PDS algorithm (Figure 1).

In the ReSiDe algorithm, the current image estimate, $$$\boldsymbol{x}_{t-1}$$$, is contaminated with complex-valued, zero-mean white Gaussian noise of variance $$$\sigma_t^2$$$ to generate a noisy image, $$$\tilde{\boldsymbol{x}}_{t-1}$$$ (Line 3). Then, we train a network by feeding it $$$P\geq1$$$ pairs of noisy-clean patches as input-output (Line 4). The noisy patches are extracted from $$$\tilde{\boldsymbol{x}}_{t-1}$$$, while the clean patches are extracted from $$${\boldsymbol{x}}_{t-1}$$$. The locations of the patches within $$$\boldsymbol{x}_{t-1}$$$ or $$$\tilde{\boldsymbol{x}}_{t-1}$$$ are selected randomly. The patch extraction is performed by the operator $$$\mathcal{I}$$$, with $$$\mathcal{I}[\cdot]_i$$$ representing the $$$i^\text{th}$$$ patch. The network is parameterized by $$$\boldsymbol{\theta}$$$, with $$$\boldsymbol{\theta}_t$$$ representing the network parameters at the $$$t^\text{th}$$$ iteration. In each iteration, the network is trained de novo from a random initialization of the network parameters. Finally, we use the trained network to denoise $$$\boldsymbol{u}_t$$$ (Line 6). Here, the operator $$$\mathcal{L}(\cdot)$$$ defines the loss function used in training; we chose $$$\mathcal{L}(\boldsymbol{a},\boldsymbol{b})=\|\boldsymbol{a}-\boldsymbol{b}\|_2^2$$$. A larger value of $$$\sigma_t^2$$$ was used in the earlier iterations to speed up convergence.

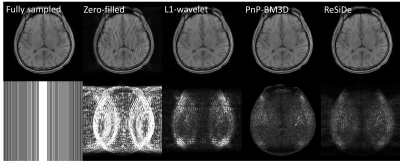
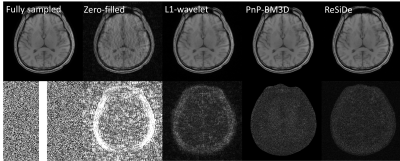
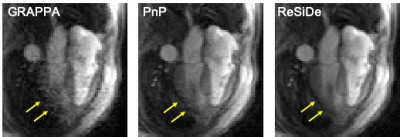
For validation, two datasets were used: a $$$320\times 320$$$ single-coil T1-weighted brain dataset downloaded from fastMRI (https://fastmri.org) and a $$$144 \times 144$$$ multi-coil first-pass perfusion (FPP) dataset acquired on a 1.5T scanner (MAGNETOM Sola, Siemens Healthcare, Erlangen Germany) using echo-planar imaging readout. The brain dataset was retrospectively undersampled at $$$R=1.8$$$ with two different sampling patterns, M1 and M2. The perfusion dataset was prospectively undersampled at $$$R=2$$$. For the brain dataset, we compared ReSiDe with two other unsupervised methods: L1-wavelet (https://mrirecon.github.io/bart) and PnP with BM3D denoiser (PnP-BM3D). For the FPP dataset, we qualitatively compared ReSiDe with GRAPPA and PnP. Since clean FPP images were not available, the denoiser in PnP was trained using 158 GRAPPA ($$$R=2$$$) image series.

Results

Figures 2 and 3 show images from the T1-weighted dataset reconstructed with two different sampling patterns, M1 and M2. The first row includes the ground truth from fully sampled k-space, zero-filled image, and recovery from L1-wavelet, PnP-BM3D, and ReSiDe. The second row shows the sampling pattern along with the corresponding error maps. Figure 4 summarizes normalized mean-squared error (NMSE) values (in dB) from different methods. On average, ReSiDe outperforms L1-wavelet and PnP-BM3D by 3.13 dB and 0.6 dB, respectively. Figure 5 shows a representative frame from the perfusion dataset, with ReSiDe providing a better suppression of noise (yellow arrows).

Discussion and Conclusion

We propose a self-calibrated method called ReSiDe. In contrast to the traditional PnP approach, where an off-the-shelf or an application-specific denoiser is used, ReSiDe iteratively trains the denoiser from the image being recovered, obviating the need for training data while enabling image-specific training of the denoiser. Our preliminary results show that ReSiDe can outperform other training-free methods, namely L1-wavelet and PnP-BM3D, in terms of image quality. For FPP, where the true image is not available, a qualitative assessment of the recovered images shows that ReSiDe is better able to suppress noise and blocky artifact, yielding a more uniform myocardium. Although the DL denoiser in the traditional PnP approach (Figure 5, middle column) was trained using 158 FPP datasets, the low signal-to-noise ratio of the training images led to noise amplification in the PnP reconstruction. Future studies will focus on a more extensive validation of ReSiDe.

Acknowledgements

This work was funded by the National Institute of Health grants R01HL135489 and R01EB029957