3479
Understanding and Reducing structural bias in deep learning-based MR reconstruction
Arghya Pal1 and Yogesh Rathi2
1Department of Psychiatry, Harvard Medical School, Boston, MA, United States, 2Harvard Medical School, Boston, MA, United States
1Department of Psychiatry, Harvard Medical School, Boston, MA, United States, 2Harvard Medical School, Boston, MA, United States
Synopsis
Deep learning methods are increasingly being used for accelerating magnetic resonance imaging (MRI) acquisition and reconstruction strategies. However, it is important to understand whether or not deep learning models have an inherent structural bias that may effectively create concerns in real-world settings. In this abstract, we show a strategy to understand and then reduce structural prior bias in deep models. The proposed approach decouples the spurious structural bias (prior) of a deep learning model by intervening in the input. Our proposed debiasing strategy is fairly robust and can work with any pre-trained deep learning MR reconstruction model.
Introduction
Deep learning has shown success in accelerating magnetic resonance imaging (MRI) acquisition and reconstruction strategies. Several ideas inspired by deep learning techniques for computer vision and image processing have been successfully applied to nonlinear image reconstruction in the spirit of compressed sensing for accelerated MRI. Given the rapidly growing nature of the field, it is imperative to study whether or not deep learning models impose strong structural bias which may hurt their generalizability and reliability in the case of real-world applications. It is shown in recent deep learning studies such as COSAIR1, VCRCNN2, etc., that the data intervention strategy may decouple such structural priors from the deep learning methods. Simply incorporating more data into the model might not help, as structural priors are mainly imposed by the learning procedure at the training time.Similar to them, we adopt an input intervention strategy to decouple spurious structural biases incorporated in the deep learning-based MR reconstruction technique. Our proposed methodology is based on the question; what will the MRI reconstruction of a deep model look like if handcrafted noisy k-space measurements such as random Gaussian noise, zero values, etc. are used as input instead of actual k-space measurements? We will use a few state-of-the-art (SOTA) methods as exemplars for this task with counterfactual k-space measurements as input. Our methodology first identifies structural prior biases and then mitigates them.
Methods
Aim: Given k-space measurements $$$y_1, y_2, \cdots, y_{n_c}$$$ coming from $$$n_{c}$$$ receiver coils undersampled with a binary mask $$$\mathbf{M}(\cdot)$$$, we study a deep learning based MR reconstruction model $$$G_{\Theta}(\cdot)$$$ that provides the reconstructed image, i.e. $$$G:\mathbb{R}^{n_c \times w \times h} \to \mathbb{R}^{c \times w \times h}$$$, that has $$$w, h$$$ as width and height respectively, and $$$c$$$ is the number of coils. We assume that the parameter $$$\Theta$$$ is learned using some SOTA algorithm (i.e. a pre-trained deep network) and the parameter $$$\Theta$$$ will remain fixed during the entire course of our study of structural prior bias understanding.Identifying the structural prior bias: Following the Bayes rule we can view the inference process as follows: $$$G(x| y_1, y_2, \cdots, y_{n_c}, \Theta)$$$, where $$$x$$$ is the MR image. It is possible that a deep model was inadvertently contaminated by some spurious structural prior during its training procedure. We actively intervene the input k-space measurements $$$y_1, y_2, \cdots, y_{n_c}$$$ with some predefined inputs to decouple the structural priors from the actual reconstruction of the deep network, see Fig 1. To elaborate, we deliberately provide handcrafted values to $$$\tilde{y}_1, \tilde{y}_2, \cdots, \tilde{y}_{n_c}$$$, such as salt-n-pepper noise, gaussian noise, zeros, etc., instead of actual k-space measurements to a deep model, i.e. $$$G(x| \tilde{y}_1, \tilde{y}_2, \cdots, \tilde{y}_{n_c}, \Theta)$$$.
Removing the Bias: We adopted a simple but effective approach to remove such bias from a deep learning model, i.e. directly subtracting the spurious structures from the actual predictions. Let’s assume that, the prediction from a deep model is $$$x$$$, i.e. $$$G(x|\tilde{y}_1, \tilde{y}_2, \cdots, \tilde{y}_{n_c}, \Theta)$$$, and the prediction is $$$\tilde{x}$$$ given the handcrafted noisy inputs. Similar to COSAIR algorithm we subtract the effect of structural prior bias by an element-wise subtraction operation, i.e. $$$c(x) = G(x| \tilde{y}_1, \tilde{y}_2, \cdots, \tilde{y}_{n_c}, \Theta) - \lambda G(x|\tilde{y}_1, \tilde{y}_2, \cdots, \tilde{y}_{n_c}, \Theta)$$$, where $$$\lambda$$$ is a hyperparameter.
Experiments
In Fig 2, we provide noise as input, i.e. salt-and-pepper noise, to SOTA methods such as JMoDL3, Deep ADMM4, UNET5, SRGAN6, Hypernetwork8 models. The models are trained using the k-space and ground truth provided in the fastMRI7 brain dataset.Fig 3 shows a quantitative comparison among SOTA methods with respect to different scales such as NMSE, PSNR, and SSIM. The left columns indicate the pre-bias scores of these models, while the right columns indicate the modified scores after adopting our proposed bias removal technique. The results may slightly vary based on the seed value chosen at the training time of these SOTA methods.
Discussion and Conclusion
In this work, we study the structure prior bias that a deep learning model may inadvertently assimilate due to the dataset imbalance, optimization procedure, etc. We specifically use the handcrafted noise to visualize such structural biases and propose a method to decouple them from the deep learning inference pipeline. The proposed method acts as post-processing to an already trained model making no overhead to the training procedure. Our experiments demonstrated the proposed method’s effectiveness to reduce bias from SOTA methods. Jointly optimizing the deep models and reducing the bias could be one of the future studies.Acknowledgements
This work is funded by NIH grant R01MH116173 (PIs: Setsompop, Rathi).References
- Chen Qian et al., Counterfactual Inference for Text Classification Debiasing, Proceedings of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th International Joint Conference on Natural Language Processing, pages 5434–5445 August 1–6, 2021. ©2021 Association for Computational Linguistics.
- Tan Wang, Jianqiang Huang, Hanwang Zhang, Qianru Sun., Visual Commonsense RCNN, CVPR, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, pages=10760--10770, 2020}
- Hemmanth Aggarwal et al., Joint Optimization of Sampling Patterns and Deep Priors for Improved Parallel MRI, ICASSP 2020.
- Yan Yang, Jian Sun, Huibin Li, Zongben Xu. Deep ADMM-Net for Compressive Sensing MRI, NIPS(2016).
- O. Ronneberger et al., U-Net: Convolutional networks for biomedical image segmentation, MICCAI, 2015.
- Christian Ledig et al, Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network, CVPR, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition.
- J. Zbontar et al. “FastMRI: An open dataset and benchmarks for accelerated MRI”. In: arXiv:1811.08839 [cs.CV]. 2018.
Figures

(Up) A deep model can be inadvertently contaminated by any spurious structural prior to its training procedure. The deep model is trained with k-space measurements. (Bottom) We actively intervene in the input k-space measurements to get such structural priors.

We provided handcrafted, i.e. salt-and-pepper noise, as input (leftmost) to different deep learning methods. We trained the hyperparameter, SRGAN networks; while, we took the pre-trained models of Deep ADMM, JMoDL, and UNET models. Given the hand-crafted noise, we note some structural bias in SOTA methods. The last column is the FFT of the input.
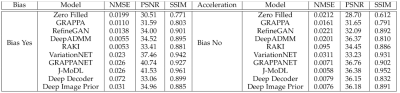
Quantitative comparison among SOTA methods with respect to different scales such as NMSE, PSNR, and SSIM, when there was bias and after bias removal.
DOI: https://doi.org/10.58530/2022/3479