Synopsis

Deep Learning based reconstruction methods have been vastly explored for accelerating Cartesian-based cardiac cine imaging via using unrolled neural networks. However, for non-Cartesian trajectories such as radial, these networks require substantial modifications (i.e., NUFFT-based data consistency) and requires collecting separate radial-based dataset, which may not be common in the clinics.

Here, we investigate a method to transfer the radial k-space data to the Cartesian domain using GROG-based interpolation. We show that DL-ESPIRiT trained with Cartesian cine dataset (with pseudo radial-like under sampling pattern) can be generalizable to reconstruct actual accelerated radial cine acquired on a scanner.

Introduction

Recently, Deep Learning (DL) based reconstruction methods have been explored for accelerating Cartesian-based cardiac cine imaging [1-2]. Specifically, DL-ESPIRiT [1], which combines ESPIRiT calibrated maps and unrolled neural network architecture, has outperformed conventional regularized iterative reconstruction, also providing accurate ventricular volumetry information across large cohorts of patients [3]. However, these DL methods are currently constrained for Cartesian-based acquisitions, and generalization for non-Cartesian trajectories (i.e., radial, spiral) requires substantial modifications.Previously, DL-based approaches for non-Cartesian trajectories have been presented either using NUFFT operations in the unrolled architecture [4] or train image-to-image based network on the pairs of outputs from gridding reconstruction [5]. Specifically, former method requires high computation burden due to NUFFT in the case of using unrolled based architecture. And both methods require collecting large fully sampled radial data which may not be common in the clinics.
Here, we investigate a completely different approach – rather than training DL reconstruction from radial data, we first preprocess the radial k-space to Cartesian grid using GROG-technique [6] (by shifting radial k-space data onto a Cartesian grid in a one-to-one mapping process) and perform DL-reconstruction in a synthesized Cartesian-gridded k-space.
In this work, we explore a framework which combines GROG interpolation with Cartesian-based DL-ESPIRiT. For the DL-ESPIRiT, the network was trained with Cartesian cine data only with radial-like under-sampling to explore the generalization of the method for actual radial trajectory. For comparison with DL-ESPIRiT, we performed NUFFT-based iGRASP reconstruction [7]

Methods

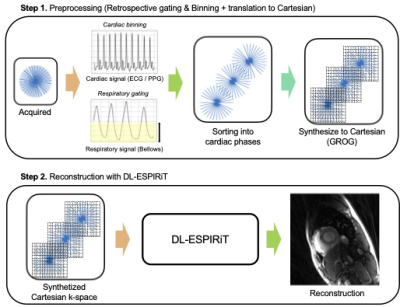
The proposed method can be summarized into two sequential steps (Fig.1.). For the first step, the acquired radial k-space is prepared by sorting into multiple cardiac phases. To account for the spurious artifacts due to motion, the respiratory signal from bellows is used to throw away k-space signals (total 50%) in the inspiratory phase. For the second step, Cartesian DL-ESPIRiT with 15 unrolls is used for the reconstruction. As the original network is trained for Cartesian 1D under-sampling pattern, we retrained the network using the radial-like under-sampling pattern, but from same dataset.

GROG interpolation
GROG interpolation shifts all radial k-space points into Cartesian grid, resulting in a synthesized Cartesian k-space with points distributed in a radial-like pattern. The process is performed as
$$S(k_x + \delta_x, k_y + \delta_y) = G_x^{\delta x} G_y^{\delta y} S(k_x,k_y) $$
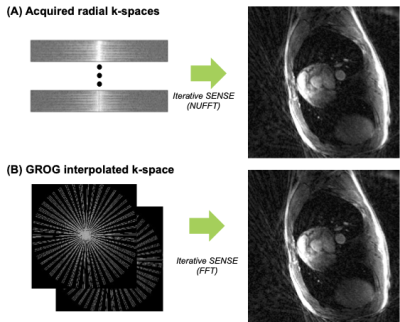
Where each radial k-space points at location [k­x,ky] is shifted to nearest Cartesian point [kx+dx, ky+dy]. The Gx, Gy are self-calibrated using acquired multi-coil radial k-space data. Figure 2 shows the current process and iterative SENSE reconstructions from each domain of k-space (Radial, Cartesian) are compared.

Training dataset
First, fully sampled bSSFP 2D cardiac Cartesian CINE data used in [1] was used to generate synthetic radial cine data. In the dataset, 240 slices were acquired from 15 volunteers at different cardiac views and slice locations on 3.0T GE (Waukesha, WI) scanners.The multi-coil radial k-space measurement was synthetized by applying random pseudo radial-like under-sampling mask, matched to the actual radial scans. To reflect motion artifact and gradient delay, we individually applied random shifting and added random linear phase in each line of the k-space.


Radial cine acquisition
To investigate the performance of the proposed method, we acquired SPGR-based continuous golden-angle based radial data [7] from two healthy volunteers. The scan parameters were as follows – TR=4.6ms, TE=2.0ms, Flip angle=15, slice thickness=5. For the fully sampled reference, the image was acquired with – FOV=350mm, number of readouts=192 (with oversampling factor of 2), total acquired spokes=19200 (1min 30s). To test on prospective under-sampled data, the image was acquired with total spokes of 3200 (15s). After respiratory signal gating and cardiac phase binning, the resulting number of spokes for binned phase were – 355 spokes (full reference) and 58 spokes (under-sampled).

Results

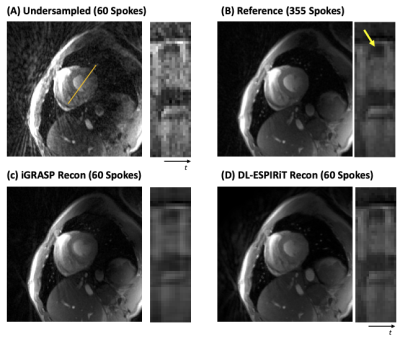
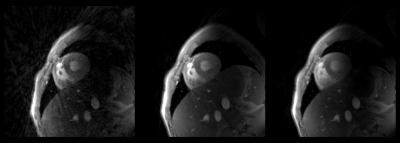
Figure 3, shows the reconstructed result from iterative SENSE, iGRASP, DL-ESPIRiT for retrospectively undersampled radial k-space (60 spokes from 355 spokes). Streaking artifacts that can be seen in (A) was both suppressed in (C) and (D). DL-ESPIRiT shows sharper temporal line profile (position marked as orange line in A) than iGRASP compared with reference (B). Figure 4, shows the reconstructed result from iterative SENSE, iGRASP, DL-ESPIRiT for prospective undersampled radial k-space (60 spokes from 355 spokes). Here, DL-ESPIRiT reconstruction contains remaining streaking artifacts compared to iGRASP, but sharper transition across cardiac phase can be observed.

Discussions and Conclusion

In this work, we present a framework which combines GROG interpolation with Cartesian-based DL-ESPIRiT. Our results suggest that Cartesian based DL-reconstruction methods can be extended for the radial trajectory by translating radial acquired k-space to Cartesian via GROG interpolation. DL-ESPIRiT which was trained with Cartesian data using pseudo-radial like undersampling pattern was generalizable for untrained radial data. However, there are some limitations in our study. DL-ESPIRiT trained with Cartesian dataset contained some remaining streaking artifacts supposedly from radial sequence (i.e., eddy current, gradient delay). We expect that fine tuning the network with some actual radial scans will further improve DL-ESPIRiT reconstruction.

Acknowledgements

NIH R01 EB009690, NIH R01 EB026136, and GE Healthcare