Introduction

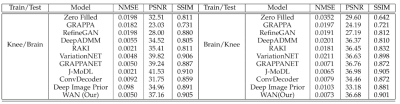
Trained deep networks such as Variational network¹ J-Model² outperform classical MR reconstruction approaches (e.g. GRAPPA, SENSE) for highly under-sampled k-space data. However, they require large datasets at training time (along with ground truth data) which may not be readily available in practice. It is also observed that such methods are not task-agnostic and perform poorly for out-of-distribution test cases such as the reconstruction of brain images from a network trained on the knee dataset. Untrained networks such as DIP³, DeepDecoder⁴, ConvDecoder⁶ on the other hand do not require explicit training but perform optimization during inference time which makes them extremely slow, requiring several minutes to process a single slice of k-space data.

In this work, we address both these challenges and propose to perform fast multi-coil MRI reconstruction using an untrained weight agnostic randomly weighted network (WAN) without the need for ground truth data. The proposed methodology offers a novel perspective to learn the mapping from under-sampled k-space to the MR image. WAN is based on the premise that a subnetwork of a very large deep neural network can encode meaningful information to solve a task even though the parameters of the network are totally random. The proposed methodology does not require any ground truth MR image (or k-space measurements) and can perform reconstruction tasks in a domain agnostic manner. We show that the proposed method outperforms the state-of-the-art (SOTA) methods such as ConvDecoder, DIP, VarNet, etc., on the fastMRI knee and brain dataset.

Methods

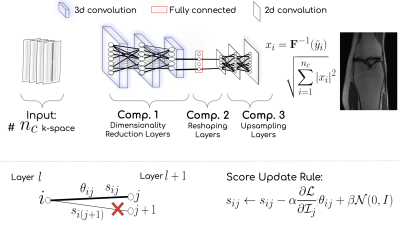
Aim: Given k-space measurements $$$y_1, y_2, ..., y_{n_c}$$$ coming from $$$n_{c}$$$ receiver coils undersampled with a binary mask $$$\mathbf{M}(\cdot)$$$, the WAN $$$G_{\Theta}(\cdot)$$$ provides the reconstructed image, i.e. $$$G:\mathbb{R}^{n_c \times w \times h} \to \mathbb{R}^{c \times w \times h}$$$, that has $$$w, h$$$ as width and height respectively, and $$$c$$$ is the number of coils. Instead of updating the weights $$$\Theta$$$ of the network, the WAN uses the edge-popup algorithm to select an optimal subnetwork using a real-valued score $$$s$$$ associated with each weight $$$\theta\in \Theta$$$.

Estimating Score Values: Similar to edge-popup5 algorithm, for any weight of either the fully connected or convolutional layer we associate a score value $$$s\in S$$$ that decides whether or not that weight is to be included in the subnetwork. The methodology drops all the weights with low score values to find a subnetwork in the parameter space $$$\Theta$$$. The score update rule: $$$s_{ij} \leftarrow s_{ij}-\alpha\frac{\partial\mathcal{L}}{\partial \mathcal{I}_{j}}\theta_{ij} + \beta\mathcal{N}(0,I)$$$. Where, $$$\theta_{ij}$$$ is output of node $$$i$$$ at layer $$$l$$$, the $$$\mathcal{I}_{j} = \sum_{i}\mathcal{Z}_{i}\theta_{ij}\psi(s_{ij})$$$ is the summed up input to node $$$j$$$ at layer $$$l+1$$$ from all nodes at layer $$$l$$$, the Gaussian noise $$$\mathcal{N}(0,I)$$$ acts as a regularizer to the update rule, and $$$\alpha, \beta$$$ are the learning rates, and $$$\psi(\cdot)=1$$$ if it has some threshold value $$$0$$$ otherwise. The weights undergo a permutation after running for a few epochs.

Architecture: WAN architecture, Fig 1, has 3 components, i.e. (1) Dimensionality Reduction Layers comprised of 3d convolution, ReLu, and batch norm; (2) Reshaping Layer is Fully Connected layer; and (3) Upsampling Layers that resembles the ConvDecoder⁶.

Learning Procedure:
Step 1: The score values are optimized by minimizing $$$\frac{1}{2}\sum_{i=1}^{n_c} \lVert \mathbf{y}_i - \mathbf{M} \mathbf{F} G_i([y_1, y_2, ..., y_{n_c}],S) \rVert_2^2$$$, keeping random weights untouched. Here, $$$\mathbf{F}$$$ is the 2D Fourier transform, $$$G_i$$$ is the $$$i$$$-th output channel of the WAN, and $$$S$$$ is the score matrix. Each $$$G_i$$$ provides inferred fully sampled k-space $$$\tilde{y}_{i}$$$$.
Step 2: We get $$$x_i = \mathbf{F}^{-1}(y_i)$$$ and the reconstructed MR image using the root-least-squares algorithm, i.e. $$$\sqrt{\sum_{i=1}^{n_c}|x_{i}|^{2}}$$$.
Step 3: Similar to ConvDecoder6 we also enforce data consistency of the resulting image.
Step 4: Repeat the procedure with different initializations and average the results.

Novelty: WAN does not update weights and only looks for a plausible subnetwork. WAN’s edge-popup algorithm has a regularizer and a permutation operation on the weights of a layer.

Results

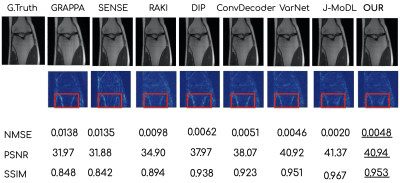
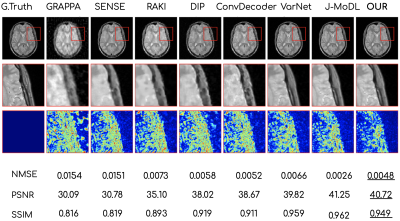
Figures 2 and 3 show the reconstruction results on the knee and brain datasets from fastMRI7.
Figure 4 illustrates an out-of-distribution example (i.e., a brain image for networks trained on knees). Other methods lose significant performance, whereas WAN, ConvDecoder, and DIP are by design robust to such shifts in the domain.

Discussion and Conclusion

This work demonstrates a novel method to solve the MR reconstruction task without ever updating the weights of the network. By design, the proposed algorithm is agnostic to different tasks in terms of SSIM, PSNR, and RMSE scores and generalizes better to out-of-distribution examples. The proposed method provides performance similar to highly trained networks, but without requiring ground truth data or abundant training datasets. The method is also very fast and can reconstruct data in real-time.

Acknowledgements

This work is funded by NIH grant R01MH116173 (PIs: Setsompop, Rathi).