3470
Deep learning-based brain MRI reconstruction with realistic noise
Quan Dou1, Xue Feng1, and Craig H. Meyer1
1Biomedical Engineering, University of Virginia, Charlottesville, VA, United States
1Biomedical Engineering, University of Virginia, Charlottesville, VA, United States
Synopsis
Fast imaging techniques can speed up MRI acquisition but can also be corrupted by noise, reconstruction artifacts, and motion artifacts in a clinical setting. A deep learning-based method was developed to reduce imaging noise and artifacts. A network trained with the supervised approach improved the image quality for both simulated and in vivo data.
Introduction
In recent years, fast imaging techniques, such as parallel imaging1-3 and compressed sensing4, have been widely employed to speed up the MRI acquisition. By under-sampling the k-space data, these methods effectively reduce the total scan time at the expense of signal-to-noise ratio (SNR). In a clinical setting, the under-sampled data can also be corrupted by motion. Recently, artificial intelligence, especially deep learning (DL), has shown great success in various medical imaging applications. In this work, we developed a DL-based method for brain MRI reconstruction with realistic “noise” that includes artifacts. Specifically, a deep neural network was designed to reduce three types of imaging artifacts: (1) Additive complex Gaussian noise, (2) In-plane motion artifacts, and (3) Parallel imaging artifacts.Methods
To train a DL model through the supervised approach, a large number of training pairs are required. The fastMRI dataset5 (https://fastmri.med.nyu.edu/) provides fully sampled multi-coil brain MRI data for T1, post-contrast T1, T2, and FLAIR modalities, which is suitable for realistic noise simulation. Random complex Gaussian noise was first generated and added to the multi-coil images. Then, a random motion profile was synthesized, which includes in-plane translations and rotations. The multi-coil images were corrupted by manipulating the k-space lines based on the motion profile. After under-sampling the k-space data with a ratio between [2, 4], the simulated image with realistic noise was reconstructed by JSENSE6, GRAPPA3, or L1-ESPIRiT7, where the JSENSE and L1-ESPIRiT implementations were from the SigPy Python package8. The ground truth was calculated from the fully sampled multi-coil images with a sum-of-squares (SoS) reconstruction, as shown in Figure 1.A 2D U-Net9 was used as our backbone network structure to remove imaging artifacts, where the convolutional kernel size is 3 × 3 and the activation function is a parametric rectified linear unit (PReLU). The input of the network is the magnitude image with realistic noise. The last layer of the network performs a 1 × 1 convolution and generates the output magnitude image. To reduce the probability of overfitting based on the global anatomy, random flips and random patch cropping were employed during training. The network was implemented in PyTorch10 and trained to minimize the structural similarity index (SSIM) loss using Adam11 optimizer with a learning rate of 0.0001 for 200 epochs. To evaluate the network performance, SSIM and peak SNR (PSNR) between ground truth and network output were calculated. In vivo T1 and T2 brain images of a healthy volunteer were acquired on a Siemens Prisma 3T scanner. The volunteer was first asked to keep still in the reference scan and then nod his/her head to corrupt the k-space data. The under-sampling ratio was set to 3 and the images were reconstructed using GRAPPA.
Results
Figure 3 shows the quantitative evaluation results of the network performance on simulated dataset. The average SSIM and PSNR of the network output were increased for all four modalities. Figure 4 shows representative slices from the simulated dataset. Compared to the input images with simulated noise, the output images showed reduced artifacts and improved image quality. Figure 5 shows the network performance on in vivo brain images. The trained network effectively suppressed the motion artifacts, especially in the T1 image.Discussion
In this study, we implemented a deep neural network method to reduce the realistic noise in brain MRI reconstruction. In the noise simulation, we considered three widely used MRI reconstruction techniques and three types of imaging artifacts. Through the supervised training, the network learned to remove the artifacts and generate images with higher quality. Future work will include testing the network with more in vivo images.Acknowledgements
No acknowledgement found.References
[1] Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999 Nov;42(5):952-62.[2] Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med. 2002 Jun;47(6):1202-10.
[3] Lustig M, Pauly JM. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magn Reson Med. 2010 Aug;64(2):457-71.
[4] Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007 Dec;58(6):1182-95.
[5] Zbontar J, Knoll F, Sriram A, et al. fastMRI: An Open Dataset and Benchmarks for Accelerated MRI. 2018. arXiv:1811.08839 [cs.CV].
[6] Ying L, Sheng J. Joint image reconstruction and sensitivity estimation in SENSE (JSENSE). Magn Reson Med. 2007 Jun;57(6):1196-202.
[7] Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS, Lustig M. ESPIRiT--an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med. 2014 Mar;71(3):990-1001.
[8] Ong F, Lustig M. SigPy: A Python Package for High Performance Iterative Reconstruction. In Proceedings of the 27th Annual Meeting of ISMRM, Montreal, Canada, 2019. p. 4819.
[9] Ronneberger O, Fischer P, Brox T. U-net: convolutional networks for biomedical image segmentation. 2015. arXiv:1505.04597 [cs.CV].
[10] Paszke A, Gross S, Massa F, et al. PyTorch: An Imperative Style, High-Performance Deep Learning Library. 2019. arXiv:1912.01703 [cs.LG].
[11] Kingma DP, Ba J. Adam: A Method for Stochastic Optimization. 2014. arXiv:1412.6980 [cs.LG].
Figures
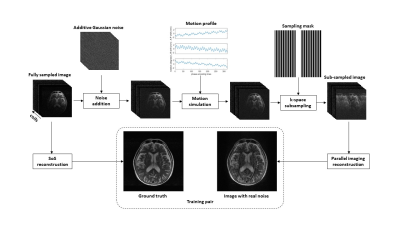
Figure 1. Generation of training data.
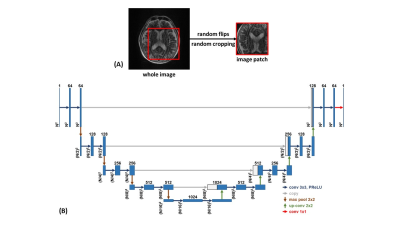
Figure 2. (A) Training augmentations, (B) U-Net architecture.
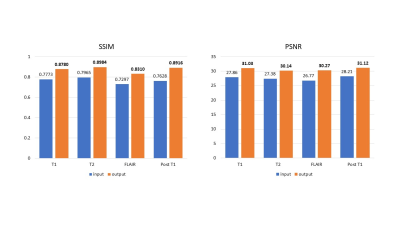
Figure 3. Quantitative evaluation results of the network performance on the simulated dataset.
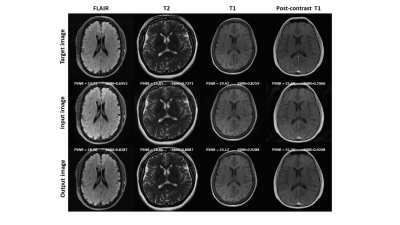
Figure 4. Representative reconstruction results on simulated data.
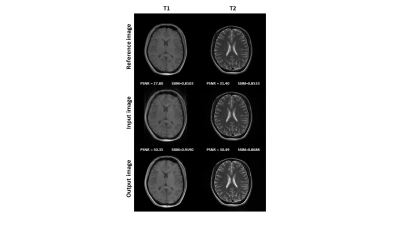
Figure 5. Network performance on in vivo data.
DOI: https://doi.org/10.58530/2022/3470