3452
Learning Deep Linear Convolutional Transforms For Accelerated MRI1Electrical and Computer Engineering, University of Minnesota, Minneapolis, MN, United States, 2Center for Magnetic Resonance Research, University of Minnesota, Minneapolis, MN, United States, 3Electrical and Computer Engineering, University of Hawai’i at Mānoa, Honolulu, HI, United States
Synopsis
Research shows that deep learning (DL) based MRI reconstruction outperform conventional methods, such as parallel imaging and compressed sensing (CS). Unlike CS with pre-determined linear representations for regularization, DL uses nonlinear representations learned from a large database. Transform learning (TL) is another line of work bridging the gap between these two approaches. In this work, we combine ideas from CS, TL and DL to learn deep linear convolutional transforms, which has comparable performance to DL and supports uniform under-sampling unlike CS, while enabling sparse convex optimization at inference time.
INTRODUCTION
Recently, many studies have shown that deep learning (DL), in particular physics-guided DL (PG-DL) methods have improved performance compared to parallel imaging1 and compressed sensing (CS)2 for accelerated MRI3, 4. CS uses a pre-specified linear representation of images for regularization, while PG-DL utilizes sophisticated non-linear representations implicitly learned through neural networks. Transfer learning (TL) is another line of work bridging the gap between these two approaches by learning linear representation from data5. DL methods use advanced optimization methods, and a large number of parameters, in contrast to the hand-tuning of two or three parameters in CS, or the more traditional optimization strategies employed in TL. On the other hand, sparse processing of linear representations used in CS/TL may provide a clearer understanding of robustness/stability6. Recent literature has aimed to address this gap by incorporating modern data science tools for improving linear representations of MR images, including denoising7 and revisiting conventional $$$\ell_1$$$-wavelet CS using state-of-the-art data science tools8. In this work, we combine ideas from CS, TL and DL for deep linear convolutional transform learning (DLC-TL). Results show that the performance gap between the proposed model and PG-DL is minimal; while our method reliably reconstructs datasets with uniform undersampling, unlike conventional CS.MATERIALS AND METHODS
Inverse Problem for Accelerated MRI: The inverse problem for accelerated MRI is given as$$\arg \min _{\mathbf{x}} \frac{1}{2}\|\mathbf{y}-\mathbf{E x}\|_{2}^{2}+\mathcal{R}(\mathbf{x})\tag{1}$$
where $$$\mathbf{y}$$$ is multi-coil k-space, $$$\mathbf{E}$$$ is forward multi-coil encoding operator1, $$$\|\mathbf{y}-\mathbf{E x}\|_{2}^{2}$$$ enforces data consistency (DC) and $$$\mathcal{R}(.)$$$ is a regularizer. In CS, $$$\mathcal{R}(\mathbf{x})$$$ is the weighted $$$\ell_1$$$-norm of transform coefficients in a pre-specified domain, such as wavelets2. In TL, $$$\mathcal{R}(\mathbf{x})$$$ uses a linear transform pre-learned from the dataset, or learned at the same time with the reconstruction5, while enforcing non-degenerate solutions with scaling constraints, or tight frame conditions5,9. This optimization is coupled over $$$\mathbf{x}$$$ and the linear transform, and run until convergence. In PG-DL, an optimization algorithm for solving (1) is unrolled for a fixed number of iterations. The regularizer in PG-DL is implemented implicitly via neural networks, while DC unit is solved linearly. The network is then trained end-to-end with appropriate loss functions, such as $$$\ell_2$$$ or $$$\ell_1$$$ norms.
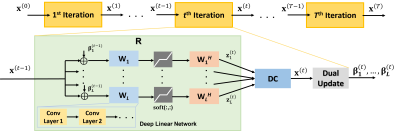
Proposed Physics-Guided Deep Linear Convolutional Transform Learning: We set $$$\mathcal{R}(\mathbf{x})=\sum_{\mathbf{n}=1}^{N} \boldsymbol{\mu}_{\mathbf{n}}\left\|\mathbf{W}_{\mathbf{n}} \mathbf{x}\right\|_{1}$$$ in (1), where $$$\mathbf{W}_\mathbf{n}$$$ are linear convolutional transforms9, and solve the objective function via unrolled ADMM for $$$T$$$ iterations (Fig. 1), leading to tunable parameters for $$$\ell_1$$$ soft-thresholding, augmented Lagrangian relaxation and dual update. These parameters and $$$\mathbf{W}_\mathbf{n}$$$ are trained end-to-end, similar to PG-DL. We encode each $$$\ell_1$$$ as a deep linear network10, featuring cascades of convolutional layers, each designed to have distinct receptive field sizes. The cascades of convolutions leverage the optimization landscape of large-scale optimization algorithms used in DL with multiple local minima11, enabling the presence of infinitely many good-performing solutions for the training objective and faster convergence12. We refer to this overall approach as deep linear convolutional transform learning (DLC-TL).
For the proposed DLC-TL, we used $$$N$$$ = 6 linear transforms and $$$T$$$ = 10 unrolls. Table 1 summarizes the network structures being implemented for each $$$\mathbf{W}_\mathbf{n}$$$. Adam optimizer with learning rate 5×10-3 was used for training over 100 epochs, with a mixed normalized $$$\ell_1$$$-$$$\ell_2$$$ loss that uses a regularizer to enforce a pseudo-tight frame condition9 on $$$\mathbf{W}_\mathbf{n}$$$. DC sub-problem for ADMM was solved using CG13 with 5 iterations and warm-start.
Imaging Data: Fully-sampled coronal proton density (PD) with and without fat-suppression (PD-FS) knee data were obtained from the NYU-fast MRI database14. The datasets were retrospectively under-sampled with a uniform mask (R=4, 24 ACS lines). Training was performed on 300 slices from 10 subjects. Testing was performed on 10 different subjects. The proposed approach was compared with PG-DL based on same ADMM unrolling that utilized a ResNet-based regularizer unit15,16. Note the only difference between the methods is the $$$\mathcal{R}(.)$$$ term, where our approach uses learnable deep convolutional operations for solving a convex problem, while the other uses a CNN for implicit regularization. An $$$\ell_1$$$-Wavelet CS approach was also used for comparison.
RESULTS
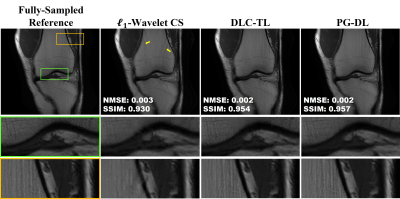
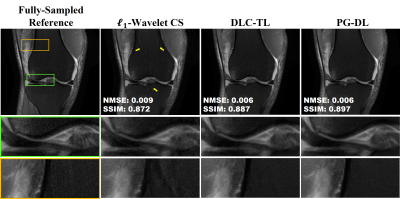
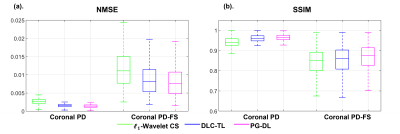
Fig. 2 and 3 show representative reconstructions from coronal PD and PD-FS knee MRI, respectively. The proposed DLC-TL and PG-DL remove aliasing artifacts that are present in $$$\ell_1$$$-Wavelet CS. As CS reconstruction typically works with random undersampling patterns, its performance is degraded with the uniform undersampling in this work. Sharpness is maintained by DLC-TL and PG-DL, whereas blurring is more apparent with $$$\ell_1$$$-Wavelet CS, especially for coronal PD-FS data. Fig. 4 depicts the quantitative metrics over all test datasets, showing the median and interquartile ranges (25th-75th percentile) of NMSE and SSIM metrics. Both the proposed DLC-TL and PG-DL outperform $$$\ell_1$$$-Wavelet CS, while having comparable quantitative metrics.DISCUSSION AND CONCLUSIONS
In this study, we proposed a combination of ideas from TL, CS and PG-DL literatures to learn deep linear convolutional transform for MRI reconstruction. While PG-DL quantitatively outperforms our approach, the performance gap is minimal. Our proposed method leads to a linear representation, and enables convex optimization at inference time.Acknowledgements
Grant support: NIH R01HL153146, NIH P41EB027061, NIH U01EB025144; NSF CAREER CCF-1651825References
1.Pruessmann K P, Weiger M, Bornert P, Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magn Reson Med. 2001;46(4):638-651.
2.Lustig M, Donoho D, Pauly J. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182-1195.
3.Knoll F, Hammernik K, Zhang C, et al. Deep-learning methods for parallel magnetic resonance imaging reconstruction. IEEE Sig Proc Mag. 2020;37(1):128-140.
4.Liang D, Cheng J, Ke Z, Ying L. Deep magnetic resonance image reconstruction: inverse problems meet neural networks. IEEE Sig Proc Mag. 2020;37(1):141-151.
5.Wen B, Ravishankar S, Pfister L, Bresler Y. Transform learning for magnetic resonance image reconstruction: From model-based learning to building neural networks. IEEE Sig Proc Mag. 2020;37(1):41-53.
6.Ye J C. Compressed sensing MRI: a review from signal processing perspective. BMC Biomed Eng. 2019;1:8.
7.Ramzi Z, Starck J, Moreau T, Ciuciu P. Wavelets in the deep learning era. in Proc. IEEE EUSIPCO. 2021;1417-1421.
8.Gu H, Yaman B, Uğurbil K, et al. Compressed sensing MRI with $$$\ell_1$$$-wavelet reconstruction revisited using modern data science tools. in Proc. IEEE EMBC. 2021.
9.Chun I Y, Fessler J A. Convolutional analysis operator learning: Acceleration and convergence. IEEE Trans Image Process. 2020;29:2108-2122.
10.Saxe A M, McClelland J L, Ganguli S. Exact solutions to the nonlinear dynamics of learning in deep linear neural networks. arXiv preprint. 2014;arXiv:1312.6120.
11.Choromanska A, Henaff M, Mathieu M, et al. The loss surfaces of multilayer networks. J Magn Reason. 2015;38:192-204.
12.Bell-Kligler S, Shocher A, Irani M. Blind super-resolution kernel estimation using an internal-GAN. in Proc. NeurIPS. 2019.
13.Aggarwal H K, Mani M P, Jacob M. MoDL: Model-based deep learning architecture for inverse problems. IEEE Trans Med Imaging. 2019;38(2):394-405.
14.Knoll F, Zbontar J, Sriram A, et al. fastMRI: A publicly avail-able raw k-space and DICOM dataset of knee images for accelerated MR image reconstruction using machine learning. Radiol AI. 2020;2(1):e190007.
15.Hosseini S A H, Yaman B, Moeller S, et al. Dense recurrent neural networks for accelerated MRI: History-cognizant unrolling of optimization algorithms. IEEE J Sel Top Signal Process. 2020;14(6):1280-1291.
16.Yaman B, Hosseini S A H, Moeller S, Ellermann J, Uğurbil K, Akçakaya M. Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data. Magn Reson Med. 2020;84:3172-3191.
Figures