Introduction

Reconstruction of image sequences is an essential step in many imaging applications such as dynamic imaging, spectroscopic imaging, and quantitative parameter mapping. A key practical challenge is the lack of sufficient k-space data per frame. To address this problem, significant efforts have been made to use a priori information to compensate for the lack of sufficient experimental data. Commonly exploited image priors include partial separability¹, image sparsity², and manifold structure^3,4 and these constraints have been successfully used separately in different reconstruction methods^1-8. This work presents a deep learning-based framework for synergistic integration of these image priors through a unified reconstruction formulation. The proposed method has been evaluated using experimental data from multi-contrast imaging, producing significantly improved reconstructions over the existing methods.

Methods

Problem Formulation
The problem of reconstructing image sequences can be formulated, in general, as follows. Given a set of sparsely sampled Fourier data points at spatial frequencies $$$\{\boldsymbol{k}_n\}_{n=1}^N$$$ and sequential indexes $$$\{t_m\}_{m=1}^M$$$:
$$\hspace{12em}d\left(\boldsymbol{k}_n,t_m\right)=\int\rho\left(\boldsymbol{x},t_m\right)e^{-i2{\pi}\boldsymbol{k}_{n}{\cdot}\boldsymbol{x}}d\boldsymbol{x}\hspace{12em}(1)$$
reconstruct $$$\rho\left(\boldsymbol{x},t_m\right)$$$. Eq. (1) can be also written in vector form as:
$$\hspace{17.5em}d=F_{\Omega}\rho,\hspace{17.5em}(2)$$
where $$$d\in\mathbb{C}^{M\times{N}}$$$ and $$$\rho\in\mathbb{C}^{M\times{P}}$$$ denote the matrix-form of measured data and desired images, respectively, and $$$F_{\Omega}$$$ represents the physical imaging operator integrating sparse sampling.

In practice, $$$\{\boldsymbol{k}_n\}_{n=1}^N$$$ very sparsely sample $$$k$$$-space for each data frame; so the inverse problem in Eq. (1) is highly under-determined. We solve this problem using a deep learning-based framework that synergistically incorporates subspace learning, manifold learning, and sparsity learning.

Proposed Reconstruction Framework
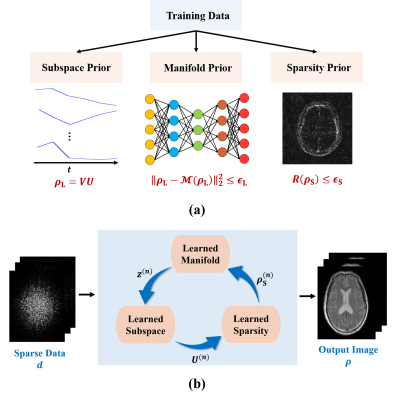
As illustrated in Fig. 1, the proposed reconstruction framework consists of two key components: a) a learning component that learns various image priors from training data, and b) an image reconstruction component that integrates the learned priors.

The learning component captured the following image priors from training data. First, a subspace representation was learned for image sequences exploiting the partial separability¹. Specifically, dominant image features were captured and represented by subspace model: $$$\rho_{\text{L}}=VU$$$ with $$$V\in\mathbb{C}^{M\times{R}}$$$ being the subspace bases and $$$U\in\mathbb{C}^{R\times{P}}$$$ the coefficients; the subspace structure was determined from training data through principal component analysis as was done in⁹. Second, the manifold structure underlying the image sequences in a training set was captured using deep learning. To this end, a deep autoencoder (DAE) was trained under the minimum mean-squared-error principle as was done in^4,10. Finally, a sparsity-promoting regularizer was learned to constrain the recovery of the novel image component $$$\rho_{\text{S}}$$$. Particularly, a neural network was trained that unrolled the gradient descent algorithm for solving the following reconstruction problem:
$$\hspace{13.5em}\min_{\rho_{\text{S}}}\left\|d_{\text{S}}-F_{\Omega}\rho_{\text{S}}\right\|_2^2+R(\rho_{\text{S}}).\hspace{13.5em}(3)$$ The resulting unrolled network, as described in^10-13, implicitly found an optimal regularization functional $$$R(\cdot)$$$ for recovery of $$$\rho_{\text{S}}$$$.

The image reconstruction component synergistically integrated the learned image priors through a physical model-based constrained reconstruction formulation:
$$\min_{\rho_{\text{L}},\rho_{\text{S}}}\left\|d-F_{\Omega}\left(\rho_{\text{L}}+\rho_{\text{S}}\right)\right\|_2^2\\{\text{subject to:}}\\\hspace{8.5em}{\rho_{\text{L}}=VU},\:\left\|\rho_{\text{L}}-\mathcal{M}\left(\rho_{\text{L}}\right)\right\|_2^2\leq\epsilon_{\text{L}},\:\text{and}\:{R}\left(\rho_{\text{S}}\right)\leq\epsilon_{\text{S}},\hspace{8.5em}(4)$$ where $$$\mathcal{M}$$$ denotes the learned DAE model. The integration of different image priors offers several advantages over the use of a single prior for image reconstruction. First, reconstruction using the subspace representation alone could be ill-conditioned due to sparse sampling, thus leading to significant image artifacts. By integrating the subspace with manifold-based prior, we could effectively constrain the image variations allowed, thus improving the performance. Second, reconstruction incorporating manifold-based prior alone may end up at some poor local minimum due to the highly non-convex nature of image manifold. This problem could be relieved by constraining the solution onto a pre-learned image subspace. Finally, the learned subspace and manifold priors enable better reconstruction of $$$\rho_{\text{L}}$$$; as a result, $$$\rho_{\text{S}}$$$ becomes much sparser, thus making the learned sparsity constraint more effective for image reconstruction.

The constrained optimization problem in Eq. (4) can be solved using the following iterative algorithm:
$$\hspace{1em}\boldsymbol{\textbf{M-step}}:\:z^{(n+1)}=\mathcal{M}\left(VU^{(n)}\right)\hspace{20em}\\\hspace{7.2em}{\boldsymbol{\textbf{U-step}}}:\:U^{(n+1)}=\arg\min_{U}\left\|d_{L}-F_{\Omega}VU\right\|_2^2+\lambda_{L}\left\|VU-z^{(n+1)}\right\|_2^2\hspace{12em}\\\hspace{1.1em}\text{with}\:d_{\text{L}}=d-F_{\Omega}\rho_{\text{S}}^{(n)}\hspace{16em}\\\hspace{1em}{\boldsymbol{\rho_{\text{S}}}\textbf{-step}}:\:\rho_{\text{S}}^{(n+1)}=\mathcal{H}_{\text{S}}\left(d_{\text{S}}\right)\hspace{21.2em}\\\hspace{8.0em}\text{with}\:d_{\text{S}}=d-F_{\Omega}VU^{(n+1)},\hspace{19.5em}(5)$$ where $$$\mathcal{H}_{\text{S}}(\cdot)$$$ is the unrolled network for recovery of $$$\rho_{\text{S}}$$$. After convergence, the final reconstruction was synthesized as: $$$\hat{\rho}=V\hat{U}+\hat{\rho}_{\text{S}}$$$.

Results

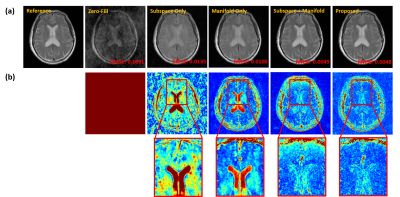
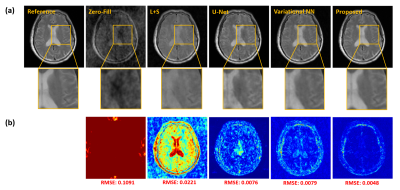
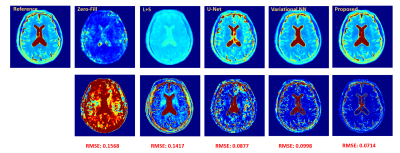
We demonstrated the proposed method in the setting of quantitative T₂ mapping. Fully-sampled images were acquired from 85 subjects on a 3T scanner using the multi-echo spin-echo sequence with the following parameters: FOV=230×230×105 mm³, matrix size=256×256×21, TR=2000 ms, and TEs=[10.5,21,31.5,42,52.5,63] ms. The images were split into 75 and 10 subjects data for model training and testing, respectively. Sparse data were generated retrospectively using a random sampling mask with an acceleration factor of R=6.

Figure 2 illustrates the effect of the priors used in the proposed method. As can be seen, both subspace and manifold priors largely reduced the aliasing artifacts over the zero-filled reconstruction, while their integration led to even greater improvement; the network-based sparsity prior picked up many residual features thus further improved the accuracy. Figure 3 compares the quality of the reconstructed images obtained by the existing methods (including both model-based and deep learning-based schemes) and the proposed method. Our method achieved the best reconstruction quality both qualitatively and quantitatively. The resulting T₂ maps are shown in Fig. 4. Again, the proposed method obtained the most accurate results.

Conclusions

We present a new deep learning-based framework for synergistically integrating learned subspace, manifold, and sparsity priors to enable high-quality reconstruction of image sequences from highly sparse data. The proposed method has been validated using experimental data, producing impressive results. It may prove useful for many MRI applications that involve the acquisition of a sequence of images.

Acknowledgements

This work reported in this paper was supported, in part, by NIH-R21-EB023413.