3447
Improved Multi-band Multi-shot Diffusion MRI Reconstruction with Joint Usage of Structured Low-rank Constraints and Explicit Phase Mapping1Departmnet of Radiology, Stanford University, Stanford, CA, United States, 2Departmnet of Radiology, University of Iowa, Iowa City, IA, United States
Synopsis
Inter-shot phase correction is a critical step in multi-band multi-shot diffusion MRI. The phase correction can be accomplished by first estimating the explicit phase map and then inputting it into the diffusion signal formulation model to recover the diffusion images. Alternatively, the phase information can be used in an indirect manner to determine structured low rank constraints in k-space. The two methods differ in terms of reconstruction accuracy and efficiency. In this study, we propose a new way to combine the two approaches for improved image quality, termed “Joint Usage of structured Low-rank constraints and Explicit Phase mapping” (JULEP).
Purpose
Inter-shot phase correction is a critical step in multi-band multi-shot diffusion MRI 1-5. The phase correction can be done by estimating the explicit phase map first and then using it in the diffusion signal formulation model2,3,4. Alternatively, the phase information can be used indirectly as structured low rank constraints in k-space. 6,7. The two methods (i.e., direct and indirect phase correction) differ in terms of reconstruction accuracy and efficiency and can also be jointly used to enhance the reconstruction performance 5. In this study, we aim to develop a new approach that combines the two methods for improved image quality, termed “Joint Usage of structured Low-rank constraints and Explicit Phase mapping” (JULEP).The diffusion signal formulation model can be described as:
$$\mathbf{d}_{i,j}=\mathbf{GF}\mathbf{S}_{j}\mathbf{P}_{i}\mathbf{I}. \left ( 1 \right )$$
where di,j is the multi-shot multi-channel diffusion k-space data, I is the diffusion magnitude, Pi is motion induced phase, Sj is the sensitivity map, F is Fourier transform, G is data under-sampling operator, i and j are the indices for shot and coil.
For direct phase-based correction, Pi is first estimated via either an external (a separately acquired navigator 2,3) or internal navigator (parallel imaging (PI) recovered image-echo from each shot 4). The resulting phase map associated with each shot is integrated into Eq. 1 to recover the clean diffusion images 2,4,8,9. The external navigator method requires an extra navigator acquisition and thus decreases the acquisition efficiency. The self-navigated method, such as MUSE 4, is more scan efficient, but the quality of navigator is dependent on the under-sampling factor in each shot (MB×Nshot).
In contrast, indirect phase correction leverages the phase correlations in a different domain. For example, in MUSSELS 6, a Hankel matrix is structured in k-space and the low rank of the Hankel matrix is used as a constraint to recover each shot (Eq. 2).
$$\underset{\mathbf{c}}{min}\left \| A\left ( \mathbf{c} \right )-\mathbf{d} \right \|_{l_{2}}^{2}+\lambda \left \| \mathbf{H\left ( \mathbf{c} \right )} \right \|_{*}. \left ( 2 \right )$$
where the first term is data consistency, the second term is low-rank regularization, c is the to-be-recovered multi-shot diffusion k-space, A is the operator to project the to-be-recovered multi-shot k-space c to the acquired multi-channel multi-shot k-space d, H(c) is the Hankel matrix, and λ
Proposed JULEP Reconstruction
The flowchart of the proposed JULEP reconstruction is shown in Fig. 1a, including:
Step i: Each shot is recovered with conventional SMS-SENSE 10 and the central recovered k-space is extracted as navigator.
Step ii: The navigator is denoised with local MUSSELS and the Hankel matrix is structured only from the central k-space, which improves the SNR of the navigator with a slightly increased reconstruction time.
Step iii: The shot-combined diffusion image is recovered using MUSE, with the denoised navigator from step ii.
Step iv: The MUSE recovered images are multiplied by the phase map of each shot to synthesize the multi-shot k-space , which is further used as the initialization of a global MUSSELS framework to improve the SNR and mitigate any residual artifacts.
Example interim images after each step are shown in Fig. 1b.Virtual coil conjugates (VCC) 11 are used in steps ii-iv for better performance. Conventional MUSE 4 and IRLS MUSSELS 6 are conducted (also with VCC) for comparisons.
Data Acquisition
Data were acquired on a GE 3.0 T Premier MRI scanner using a 48-channel head coil. A single-band 2D diffusion prepared 4-shot interleaved EPI sequence was used for data acquisition, with detailed parameters in Fig. 1c. To quantify the image quality difference caused only by the reconstruction, MB=2 and 3 data were simulated from the MB=1 acquisition.
Results
Fig. 2 shows (a) single-direction diffusion images, (b) averaged MB=1 diffusion images as reference and (c) difference maps between each result and reference. From the difference maps, JULEP maintains the most consistent results with the reference. Aliasing is the main residual artifacts in the MUSE results, while the MUSSELS results are noisier. These artifacts can further result in lower tSNRs in the MUSE and MUSSELS results compared with JULEP (yellow arrows in Fig. 3).The FA and MD maps from different MB acceleration factors and reconstruction methods are shown in Fig. 4 and 5, respectively. The findings are consistent with the single-direction diffusion images and tSNR maps. In the FA maps, at MB=3, the anterior commissure is most clearly visible in the JULEP result (yellow arrows). From MD maps, the bias is also best mitigated using the proposed JULEP method when MB=3, compared with MUSE and MUSSELS.
Discussion & Conclusion
The proposed JULEP method significantly improves the reconstruction quality of multi-band multi-shot diffusion MRI, which can promote a broader applications of high-resolution diffusion MRI.Acknowledgements
This study is funded by GE Healthcare, the Focused Ultrasound Foundation and an RSL Neuro seed grant.
References
1. Miller KL, Pauly JM. Nonlinear phase correction for navigated diffusion imaging. Magn Reson Med 2003;50:343-353.
2. Ma X, Zhang Z, Dai E, Guo H. Improved multi-shot diffusion imaging using GRAPPA with a compact kernel. Neuroimage 2016;138:88-99.
3. Jeong HK, Gore JC, Anderson AW. High-resolution human diffusion tensor imaging using 2-D navigated multishot SENSE EPI at 7 T. Magn Reson Med 2013;69:793-802.
4. Chen NK, Guidon A, Chang HC, Song AW. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE). Neuroimage 2013;72:41-47.
5. Bilgic B, Chatnuntawech I, Manhard MK, et al. Highly accelerated multishot echo planar imaging through synergistic machine learning and joint reconstruction. Magn Reson Med 2019;82:1343-1358.
6. Mani M, Jacob M, Kelley D, Magnotta V. Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS). Magn Reson Med 2017;78:494-507.
7. Mani M, Jacob M, McKinnon G, et al. SMS MUSSELS: A navigator-free reconstruction for simultaneous multi-slice-accelerated multi-shot diffusion weighted imaging. Magn Reson Med 2020;83:154-169.
8. Chu ML, Chang HC, Chung HW, et al. POCS-based reconstruction of multiplexed sensitivity encoded MRI (POCSMUSE): A general algorithm for reducing motion-related artifacts. Magn Reson Med 2015;74:1336-1348.
9. Dai E, Zhang Z, Ma X, et al. The effects of navigator distortion and noise level on interleaved EPI DWI reconstruction: a comparison between image- and k-space-based method. Magn Reson Med 2018;80:2024-2032.
10. Koopmans PJ. Two-dimensional-NGC-SENSE-GRAPPA for fast, ghosting-robust reconstruction of in-plane and slice-accelerated blipped-CAIPI echo planar imaging. Magn Reson Med 2017;77:998-1009.
11. Blaimer M, Gutberlet M, Kellman P, et al. Virtual coil concept for improved parallel MRI employing conjugate symmetric signals. Magn Reson Med 2009;61:93-102.
Figures
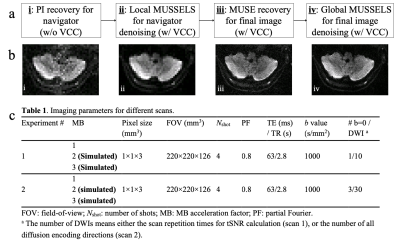
Figure 1: (a) The flowchart of JULEP reconstruction. (b) Example images after each step of the JULEP reconstruction. (c) Detailed imaging parameters in this study.
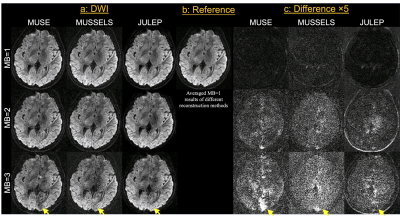
Figure 2: (a) Single-direction diffusion images with different MB factors (MB=1, 2 and 3) and reconstruction methods (MUSE, MUSSELS and JULEP). (b) The average of MB=1 diffusion images is used as the reference. (c) The difference maps between each single-direction image and the reference images. Yellow arrows indicate severer residual artifacts in MUSE and MUSSELS results at MB=3.
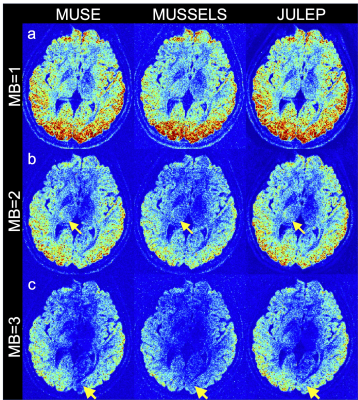
Figure 3: Temporal SNR (tSNR) results from different reconstruction methods (MUSE, MUSSELS and JULEP) at (a) MB=1, (b) MB=2 and (c) MB=3. Yellow arrows indicate higher tSNR in the JULEP results compared with the other two methods.
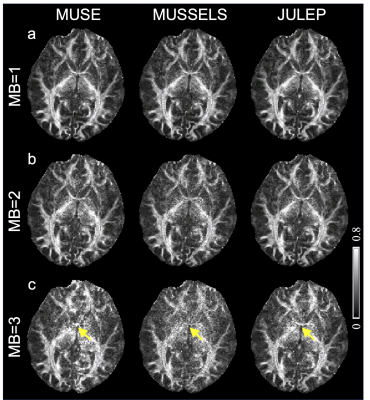
Figure 4: Fractional anisotropy (FA) maps from different reconstruction methods (MUSE, MUSSELS and JULEP) at (a) MB=1, (b) MB=2 and (c) MB=3. Yellow arrows indicate the anterior commissure, which is most clearly visible in the JULEP result when MB=3.
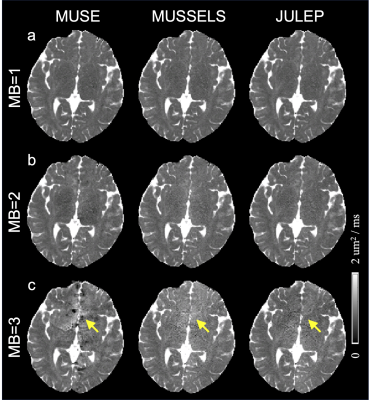
Figure 5: Mean diffusivity (MD) maps from different reconstruction methods (MUSE, MUSSELS and JULEP) at (a) MB=1, (b) MB=2 and (c) MB=3. Yellow arrows indicate the hypo-MD values in the MUSE result and visually higher MD values in the MUSSELS result when MB=3.