Introduction

The standard dual-input, two-compartment model of studying liver function with dynamic gadoxetate-enhanced MRI requires the hepatic artery (HA) input for liver function measurements^1,2. It is a challenge to measure the dynamic contrast agent concentration in the HA due to the small size of the HA, and instead the dynamic contrast agent concentration in abdominal aorta (AA) is measured and used as the arterial input function, assuming that the two concentrations are the same except a time delay of the former. In this study, we determined the relationship between these two concentrations.

Theory

In a blood vessel at position x, the total derivative of contrast agent concentration C(x,t) with respect to time t is governed by the equation:

dC(x,t)/dt = ∂C(x,t)/∂t + V(x,t)∙∂C(x,t)/∂x = -C(x,t)·∂V(x,t)/∂x (1)

where ∂C(x,t)/∂t and ∂C(x,t)/∂x are the partial derivate of C(x,t) with respect to t and x, respectively (Fig. 1). V(x,t) is the blood flow velocity. For constant blood flow V, we have dC(x,t)/dt = 0 or ∂C(x,t)/∂t = -V∙∂C(x,t)/∂x, i.e., a temporal increase in C(x,t) is accompanied with a spatial decrease in C(x,t), and vice versa. The solution is C(x₂,t+ẟt) = C(x₁,t) with ẟt = (x₂ – x₁)/V. However, for an increased blood flow, i.e., ∂V(x,t)/∂x > 0, it reduces C(x,t) as shown in Eq. (1), and this reduction in C(x,t) should result in a reduced DCE-MRI signal. The DCE-MRI time signal S(x,t) is related to C(x,t) by the FLASH equation³:

S(x,t) = ρ₀sin(θ)[1 - e^{-TR·R₁(x,t)}]/[1 - cos(θ)·e^-TR·R1(x,t)] (2)

where R₁(x,t) = R₁(x,0) + α∙C(x,t), TR is the repetition time, θ is the flip angle, R₁(x,0) is the pre-contrast longitudinal relaxation rate of water, and α is the relaxivity associated with the contrast agent. For constant blood flow with assumption of R₁(x₂,0) = R₁(x₁,0), we found

S(x₂,t+δt)/S(x₂,0) = S(x₁,t)/S(x₁,0) (3)

where S(x,0) is the pre-contrast signal intensity.

Methods and Materials

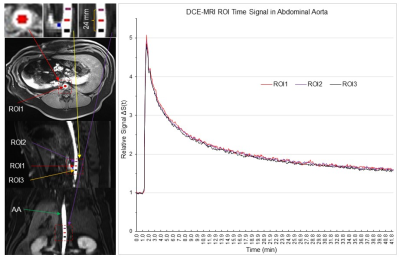
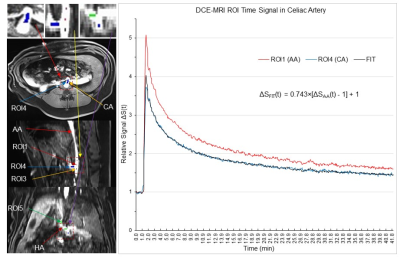
Six pigs underwent a 42.35 min DCE-MRI scan (Siemens 1.5T scanner, vibe pulse sequence, TE/TR=1.77/3.65 ms, FA=12°, FOV=320mm, matrix 256x256, 64 slices with slice thickness 3mm, 3.51s acquisition time for each image volume, and 724 volumes). Two scans were performed with Gd-EOB-DTPA injection, two were performed with Gd-DTPA injection and the other two were performed with Gd-BOPTA injection. We performed three region of interest (ROI) analyses using AFNI⁴. (i): To test Eq. (3), three ROIs with 27 voxels each were placed in the abdominal aorta. The 1^st ROI was placed right above the celiac artery (CA), the 2^nd ROI with a distance of 12 mm was placed above the 1^st ROI, and the 3^rd ROI with the same 12 mm distance was placed below the 1^st ROI (Fig. 2). (ii): The diameter of CA is less than half of that of AA, and this substantially reduced size from AA to CA may increase V(x,t) from AA to CA, resulting in a reduced S(x,t) from AA to CA as discussed above. To test this prediction, the 4^th ROI with 27 voxels was placed in the CA just outside the AA (Fig. 3). (iii): The 5^th ROI with 27 voxels was placed within the HA to determine the relationship of S(x,t) between the HA and AA (Fig. 4).

Results and Discussion

For each of the five ROIs in each scan, the mean signal S(t) averaged over all 27 voxels within that ROI was first computed, followed by computing its baseline mean signal S(0) averaged over the baseline period (22 time points), and then measuring their relative signal, i.e., ΔS(t)=S(t)/S(0). Then, we computed the group-mean ΔS(t) averaged over the six subjects. Fig. 2 illustrates this group-mean ΔS_AA(t) for the three ROIs in the AA. These three time signals were almost identical. As the blood flow velocity in arteries is ranged from 49 – 190 mm/s, the maximum time (ẟt) it takes to pass the 24 mm distance should be 0.49s that is much smaller than the 3.51s temporal resolution of the DCE-MRI. The blood flow velocity in this part of the AA was most likely the same under the well-controlled experimental condition. Accordingly, the almost identical ΔS_AA(t) in these three ROIs are consistent with Eq. (3). Fig. 3 illustrates the group-mean ΔS_CA(t) in the CA and Fig. 4 illustrates ΔS_HA(t) in the HA, respectively. The magnitude of ΔS_CA(t) was clearly reduced relative to ΔS_AA(t), consistent with our prediction. To compute this reduction rate (R), we first computed the ratio of [ΔS_CA(t) - 1] to [ΔS_AA(t) - 1] for each time point for the post-contrast period, and then its mean and SD, resulted in R=0.743±0.030. The magnitude of ΔS_HA(t) was further reduced as shown in Fig. 4, and R=0.705±0.032. Using the mean R value, the curve ΔS_FIT(t) = R∙[ΔS_AA(t) - 1] +1 is almost identical to the reduced ΔS(t) for both CA and HA, showing a quantitative relationship of contrast agent concentration between AA and both CA and HA, respectively. In conclusion, the measured arterial input function in AA can be reliably used as the HA input function with the reduction factor R taken into account.

Acknowledgements

No acknowledgement found.