Introduction

Myelin water imaging (MWI) is a promising biomarker for assessing demyelinating diseases such as multiple sclerosis¹. Multi-echo gradient-echo (mGRE) images have been used to investigate multiple T2* components and myelin water fraction (MWF) is estimated by relative ratio of the myelin water component and the sum of entire water components². One challenge of mGRE-MWI is image degradation due to artifacts and noise³. Recently, it has been demonstrated that the linear dimensionality reduction (LDR) of the mGRE images can resolve this challenge. By representing a high-dimensional dataset with intrinsic dimensionality, features that do not reside in the low-dimensional subspace can be excluded. The anomaly sources are separated to sparse component and LDR-MWF has shown robustness against noise and artifacts⁴. However, owing to the lack of orthogonality, LDR-MWF investigates only magnitude signals and cannot contain phase information of mGRE. It is necessary to consider the phase information in mGRE images to reflect structural dependencies and susceptibility anisotropies according to the relative orientation between the main field and white matter fibers⁵. In this work, we propose a nonlinear dimensionality reduction (NLDR) using deep neural networks for mapping complicated features including phase information that are not revealed in the linear subspace⁶. The proposed technique separates the spatio-temporal complex-valued mGRE signals into three lower-dimensional features, each of which represents myelin, axonal, and extracellular water signals. Also, the anomalies were extracted into sparse features. Finally, the MWF is mapped as L₁/(L₁+L₂+L₃)⁷.

Theory

Complex-valued nonlinear least squares (NLLS) algorithm for MWI:
The voxel-wise T2* decaying complex-valued signal, s(t), is fitted to the three-component complex-valued model as follows³: $$s(t)=(A_{my}exp{-(1/T_{2,my}^*+i2\pi\triangle f_{bg+my})t}+A_{ax}exp{-(1/T_2,ax^*+i2\pi\triangle f_{bg+ax})t}+A_{ex}exp{-(1/T_2,ex^*+i2\pi\triangle f_{bg+ex})t})exp{-i\phi_{0}} (eq. 1)$$ where $$$A_{my}$$$, $$$A_{ax}$$$, and $$$A_{ex}$$$ are the amplitudes of the three water components, $$$T_{2,my}^*$$$, $$$T_{2,ax}^*$$$, and $$$T_{2,ex}^*$$$ are T2* values of the three water components, $$$\triangle f_{bg+my}$$$, $$$\triangle f_{bg+ax}$$$, and $$$\triangle f_{bg+ex}$$$ are the frequency offsets of the three water components plus the sum of the background frequency offset. The amplitude, T2*, and frequency offset of each water component are estimated by NLLS errors using an iterative nonlinear curve-fitting algorithm⁸.
Linear Dimensionality Reduction (LDR) for MWI:
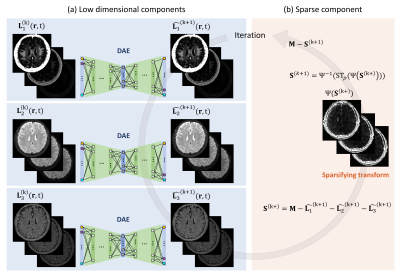
The LDR-MWF algorithm separates the spatio-temporal mGRE data into two rank-1 components (i.e., L₁ and L₂) and an additional sparse component (i.e., S) by solving the optimization problem as follows⁴: $$\min_{L_1,L_2, S}||M-\sum_{i=1}^{2}{L_i}-S||_{2}^{2}+\sum_{i=1}^{2}\mu_i||H({L_i})||_*+\rho||\psi(S)||_1 (eq. 2)$$
where $$$L_1, L_2, S \in R_{+}^{Ns × Nt}$$$, $$$||\cdot||_*$$$ denotes Nuclear norm, $$$||\cdot||_1$$$ denotes the l-1 norm, $$$|H(\cdot)$$$ denotes a hankelization operator that promotes temporal low-rankness, and $$$\psi(\cdot)$$$ denotes the temporal sparsifying operator (1D FFT in the echo domain). and $$$\mu_1$$$, $$$\mu_2$$$, and $$$\rho$$$ denote the regularization parameters for low-rankness and sparsity, respectively. MWF can be calculated as the ratio of the fast-decaying rank-1 component to the total rank-1 component at TE1 as L₁/(L₁+L₂).
Non-Linear Dimensionality Reduction (NLDR) for MWI:
The NLDR-MWF algorithm separates three nonlinear low-dimensional sources (corresponding to myelin, extracellular, and axonal water signals) and a sparse source from a complex-valued mGRE dataset. This was performed to preserve the robustness of the fiber orientation anisotropy in the NLLS-MWF while mitigating the anomaly corruption in the LDR-MWF. The optimization problem is defined as follows⁷: $$\min_{\theta_{Ei},\theta_{Di}, S}\sum_{i=1}^{3}||L_i-D(E(L_i;\theta_{Ei});\theta_{Di})||_{2}^{2}+\rho||\psi(S)||_1 (eq. 3)$$
$$$i$$$ denotes the index of the low-dimensional sources, $$$E$$$ and $$$D$$$ denote the encoder and decoder operators, respectively, $$$\theta_{Ei}$$$ and and $$$\theta_{Ei}$$$ denote the parameters of the encoding and decoding layers (i.e., weights and biases). For each of the three autoencoders, the size of the layer was set as 2Nt-30-10-5(Nf)-10-30-2Nt, and the number of epochs was set to five. The leaky rectified linear unit (ReLU) activation function was implemented in the hidden layers, except the last layer.

Methods

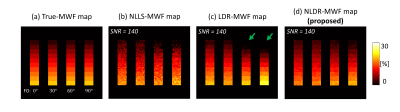
Numerical Simulation:
The hollow cylinder fiber model was used to consider phase information of mGRE images according to the relative orientation between the main field and white matter fiber⁵. The relative orientation, referred to here as the fiber orientation (FO), varied across 0°, 30°, 60°, and 90°.
Data Acquisition:
The 3D bipolar readout mGRE sequence was used to acquire the data. The values of the 3D mGRE imaging parameters were as follows: field of view (FOV) = 256×256×80 mm³, spatial resolution = 2×2×2 mm³, TR = 46 ms, TE1 = 1.65 ms, ΔTE = 1.04 ms, number of echoes = 30, flip angle (FA) = 20°, bandwidth = 1560 Hz/pixel, and total scan time = 3 min 55sec.

Results

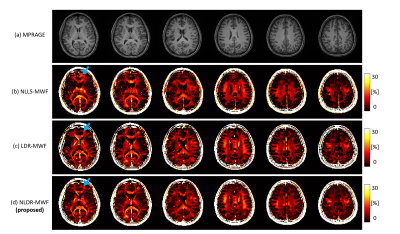
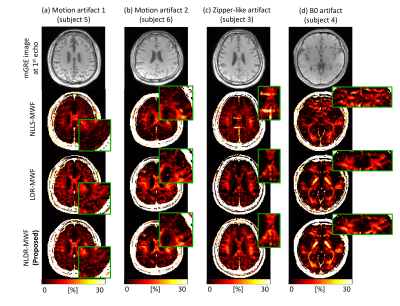
In simulation, the STD of the LDR-MWF and NLDR-MWF was reduced by approximately 40% compared to that of NLLS-MWF (Fig. 2). For FO with 60° and 90°, the LDR-MWF showed a significant underestimation (green arrow in Fig. 2c). In healthy volunteer, the boundary of the white matter was more clearly visualized in the LDR/NLDR-MWF than in the NLLS-MWF (Fig. 3). In artifact corrupted cases, the artifacts in the NLLS-MWF are reduced in the LDR-MWF and NLDR-MWF (Fig. 4).

Discussion and Conclusion

We presented a nonlinear dimensionality reduction method for MWF mapping. The low dimensionality feature is extracted using a deep autoencoder while encouraging the sparsity of the residuals. The proposed method maintains the robustness for noise and artifacts in the linear dimensionality reduction approach and improves the accuracy of the MWF map by considering complex-valued attributes.

Acknowledgements

No acknowledgement found.