3301

Mr CSD – Motion-robust Constrained Spherical Deconvolution for multi-shell multi-tissue brain modelling of infants and other restless patients

Viljami Sairanen¹
¹BABA Center, Pediatric Research Center, Department of Clinical Neurophysiology, Children’s Hospital, Helsinki University Hospital and University of Helsinki, University of Helsinki, Helsinki, Finland

Synopsis

Investigation of brain structure of infants or other uncooperative patients using diffusion-weighted MRI is challenging due to subject motion artefacts. This work proposes a novel robust augmentation to current state-of-the-art multi-shell multi-tissue (MSMT) constrained spherical deconvolution (CSD) pipeline that accounts for these artefacts in both response function estimation and in deconvolution. A proof-of-concept is shown using multi-shell infant dataset and it is compared against the normal MSMT-CSD. The results indicate that motion artefacts can result in incorrect tissue type segmentations and fiber orientation distribution (FOD) estimates which could affect negatively any following analysis such as tractography or microstructural brain modelling.

Introduction

Constrained spherical deconvolution (CSD) of diffusion-weighted images (DWI) is used to investigate voxel-wise fiber orientation distributions (FOD) in brain white matter (WM). FOD information can be subsequently used to investigate structural connectivity and microstructural properties of the brain. CSD process consist of two parts: 1) response function (RF) estimation and 2) DWI deconvolution. Multi-shell data helps to distinguish tissue types and increase FOD estimation accuracy^1-4. While CSD is sensitive to noise⁵, effects from other sources of uncertainty e.g. subject motion artefacts have not been investigated in-depth previously.

Subject motion during acquisition can result in a missing data problems⁶, which are observed as dark slices. In statistics, two distinct approaches are used to ameliorate missing data problems: imputation^7-9 (outlier replacement) or robust modelling^6,10. The problem in latter is it requires robust estimators i.e. modifications to computational algorithms. Therefore, it is more tedious to implement in practice. Whereas with imputation, one can use normal estimators to process data. This ease-of-use comes with the price of excess noise propagation due to successive modelling and statistical dependency between imputed and non-imputed data. It is not known which approach is more suitable for DWI processing. Therefore, it is necessary to formulate novel robust algorithms to evaluate the differences.

This study proposes robust augmentations to current state-of-the-art multi-shell multi-tissue (MSMT) CSD pipeline implemented in DIPY-library¹¹. While robust estimators have been applied in tensor¹⁰, microstructural¹², and single-shell CSD¹³ modelling, in the context of MSMT-CSD this is likely the first robust modelling attempt. Augmentations consider RF estimation and CSD. Motion-robust CSD could be helpful in clinical studies in which subjects might not always stay still during scan. Importantly, this is a necessary update for CSD methods so both robust approaches can be properly evaluated in the future.

Methods

The proposed robust MSMT-RF estimation is based on outlier informed kurtosis tensor estimator REKINDLE¹⁰. First step in this approach is to quantify the number of outlier slices in data using SOLID-algorithm⁶. SOLID detects slice-wise artefacts in DWIs and reports them as voxel-wise maps. Second step is to perform robust kurtosis tensor¹⁴ fit to obtain FA and MD maps to segment different tissue types. Third step is to select the most reliable voxels from these segments from which the RFs are calculated. The currently available RF estimators do not consider this measurement unreliability and therefore this update has potential to improve any MSMT-CSD pipeline if data contains subject motion artefacts.

The proposed robust CSD is designed as a convex quadratic programming (QP) problem¹ which is augmented with measurement reliability weights $$$\mathbf{W}$$$:
$$\hat{\mathbf{x}}=\min_{\mathbf{x}}\left( 0.5\mathbf{x}^{\top} \mathbf{H}_{rw} \mathbf{x} + \mathbf{f}^{\top}_{rw} \mathbf{x} \right) \textrm{ subject to } \mathbf{Ax} \geq0,$$
where $$$\mathbf{x}$$$ is the unknown FOD coefficient vector, robustly weighted $$$\mathbf{H}_{rw}=\mathbf{X}^{\top}\mathbf{WX}$$$ relates FOD design matrix $$$\mathbf{X}$$$ to each tissue type per shell, and $$$\mathbf{f}_{rw}=-\mathbf{X}^{\top}\mathbf{Wy}$$$ relates FOD to measurements $$$\mathbf{y}$$$ and $$$\mathbf{A}$$$ relates FOD coefficients to corresponding amplitudes.

In traditional matrix multiplication, the reliability weights would fill only the diagonal $$$\mathbf{w}$$$ of the weight matrix $$$\mathbf{W}$$$. As weights are unique for each voxel, this can lead into memory issues. To avoid this, the proposed method uses Einstein summation which also increases the computational speed of the matrix operations. With a suitable GPU card and Tensorflow library, matrix multiplications become nearly instantaneous and $$$\mathbf{H}_{rw}$$$ and $$$\mathbf{f}_{rw}$$$ can be precomputed rapidly for the QP-problem solver.
$$\mathbf{H}_{rw}=\textrm{tf.einsum}\left('jk, ijk \rightarrow ikl',\mathbf{X}, \textrm{tf.einsum}\left('ij, jk \rightarrow ijk', \mathbf{w}, \mathbf{X} \right) \right)$$
$$\mathbf{f}_{rw}=\textrm{tf.einsum}\left('jk, ij \rightarrow ik',\mathbf{X}, \textrm{tf.einsum}\left('ij, ij \rightarrow ij', \mathbf{w}, \mathbf{y} \right) \right)$$
In the case of full-reliability in all voxels i.e. $$$\mathbf{w}$$$ is a vector of ones, this formulation reduces to the normal QP problem¹.
The preliminary results from the comparison between the proposed Mr CSD pipeline and normal MSMT-CSD were evaluated using data from an extremely preterm born infant. Infant data ($$$13\times b=0\textrm{ s/mm}^2$$$, $$$60\times b=750\textrm{ s/mm}^2$$$, $$$74\times b=1800\textrm{ s/mm}^2$$$) was denoised¹⁵, correct for Gibbs-ringing¹⁶, motion, eddy currents and bias-fields using MRTrix3¹⁷, ANTs¹⁸ and ExploreDTI+SOLID^6,19.

Results

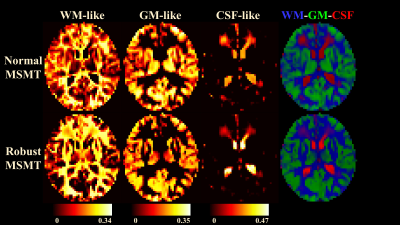
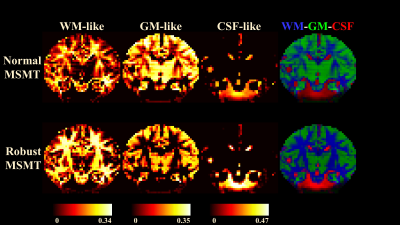
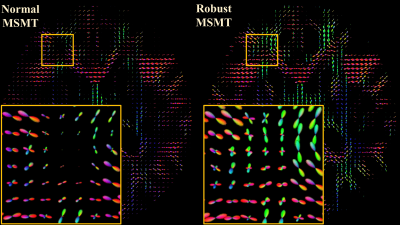
Fig.1 demonstrate the differences between normal and robust MSMT to distinguish different tissue types. The normal pipeline estimates the white matter content of thalami incorrectly whereas the robust pipeline correctly reports thalami containing both white and grey matter. This suggests that the robust augmentation is beneficial. Fig.2 visualizes the impact of the slice-wise outliers in MSMT modelling.

FODs shown in Fig.3 indicate that slice-wise outliers have potential to cause severe problems in tractography algorithms if not accounted for. Normal MSMT fails to model FODs in a region with known fiber crossings whereas robust MSMT identifies crossings correctly. Peaks shown in Fig. 4 reveal that normal MSMT could also lead to a high number of spurious streamlines in tractography due to large number of implausible peaks.

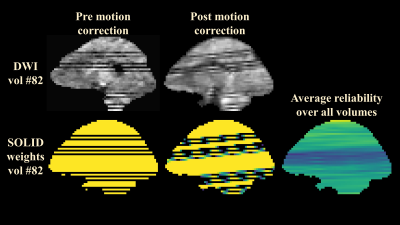
The summary of outlier detection (Fig. 5) shows that the middle parts of the brain were most heavily affected which is also seen in the normal MSMT results of Fig. 2.

Conclusion

The proposed robust augmentation to MSMT-CSD pipeline produced very promising results improving both the tissue segmentation and FOD estimation. This work should be seen as a proof-of-concept and further investigations about e.g. maximal number of outliers, comparison to imputation, and implications in tractography remains to be investigated.

Acknowledgements

No acknowledgement found.

References

1. Jeurissen, Ben, et al. "Multi-tissue constrained spherical deconvolution for improved analysis of multi-shell diffusion MRI data." NeuroImage 103 (2014): 411-426.

2. Dhollander, Thijs, David Raffelt, and Alan Connelly. "Unsupervised 3-tissue response function estimation from single-shell or multi-shell diffusion MR data without a co-registered T1 image." ISMRM Workshop on Breaking the Barriers of Diffusion MRI. Vol. 5. No. 5. ISMRM, 2016.

3. Dhollander, Thijs, et al. "Feasibility and benefits of 3-tissue constrained spherical deconvolution for studying the brains of babies." Proceedings of the 26th annual meeting of the International Society of Magnetic Resonance in Medicine. 2018.

4. Dhollander, T., et al. "Improved white matter response function estimation for 3-tissue constrained spherical deconvolution." Proc. Intl. Soc. Mag. Reson. Med. Vol. 555. 2019.

5. Tournier, J-Donald, Fernando Calamante, and Alan Connelly. "Robust determination of the fibre orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution." Neuroimage 35.4 (2007): 1459-1472.

6. Sairanen, Viljami, Alexander Leemans, and Chantal MW Tax. "Fast and accurate Slicewise OutLIer Detection (SOLID) with informed model estimation for diffusion MRI data." Neuroimage 181 (2018): 331-346.

7. Schafer, Joseph L. "Multiple imputation: a primer." Statistical methods in medical research 8.1 (1999): 3-15.

8. Koch, Alexandra, et al. "SHORE‐based detection and imputation of dropout in diffusion MRI." Magnetic resonance in medicine 82.6 (2019): 2286-2298.

9. Andersson, Jesper LR, et al. "Incorporating outlier detection and replacement into a non-parametric framework for movement and distortion correction of diffusion MR images." Neuroimage 141 (2016): 556-572.

10. Tax, Chantal MW, et al. "REKINDLE: robust extraction of kurtosis INDices with linear estimation." Magnetic resonance in medicine 73.2 (2015): 794-808.

11. Garyfallidis, Eleftherios, et al. "Dipy, a library for the analysis of diffusion MRI data." Frontiers in neuroinformatics 8 (2014): 8.

12. Sairanen, Viljami, et al. "Incorporating outlier information into diffusion MR tractogram filtering for robust structural brain connectivity and microstructural analyses." bioRxiv (2021).

13. V. Sairanen and C. M. W. Tax, “‪Robust residual bootstrapping algorithm for accurate SH representation of DW MRI signal that contains outliers,” Proc. Intl. Soc. Mag. Reson. Med. 2021

14. Jensen, Jens H., et al. "Diffusional kurtosis imaging: the quantification of non‐gaussian water diffusion by means of magnetic resonance imaging." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 53.6 (2005): 1432-1440.

15. Veraart, Jelle, et al. "Denoising of diffusion MRI using random matrix theory." Neuroimage 142 (2016): 394-406.

16. Kellner, Elias, et al. "Gibbs‐ringing artifact removal based on local subvoxel‐shifts." Magnetic resonance in medicine 76.5 (2016): 1574-1581.

17. Tournier, J-Donald, et al. "MRtrix3: A fast, flexible and open software framework for medical image processing and visualisation." Neuroimage 202 (2019): 116137.

18. Avants, Brian B., Nick Tustison, and Gang Song. "Advanced normalization tools (ANTS)." Insight j 2.365 (2009): 1-35.

19. Leemans, A. J. B. S. J. J. D. K., et al. "ExploreDTI: a graphical toolbox for processing, analyzing, and visualizing diffusion MR data." Proc Intl Soc Mag Reson Med. Vol. 17. No. 1. 2009.

Figures

Fig. 1 An axial slice demonstrating the differences between normal and robust MSMT-CSD. Reasoning why the robust fit is better can be found from e.g. thalami which are located in the central part of each sub figure. The normal MSMT labels thalami as nearly completely grey matter whereas the robust MSMT labels thalami partially white and grey matter. As the known anatomy (e.g. internal medullary lamina that is Y-shaped white matter in thalamus) provides support only for the latter, there is evidence that the robust approach is more capable to provide accurate tissue type segmentation.

Fig. 2 A coronal slice demonstrating the differences between normal and robust MSMT-CSD. Similar white and grey matter partial voluming effects as seen in Fig. 1 are observed here as well. The coronal plane visualizes the fitting error caused by the slice-wise subject motion artefacts. Both, white and grey matter estimates of the normal MSMT contain semi-vertical stripes in the same spatial location that contained the largest number of outlier slices. Due to subject motion correction (volume-to-volume rotations), outlier slices are oblique and not completely axial.

Fig. 3 Fiber orientation distributions (FOD) obtained from normal and robust MSMT. FOD amplitudes were in general higher and orientations of the FOD glyphs seem to follow known anatomy better in the robust MSMT. A highlighted section in the orange rectangle visualizes a region with known crossing-fiber populations. The normal MSMT fails modelling this regions resulting in three completely black voxels. Any tractography algorithm relying on such FOD would likely result in incorrect streamline reconstructions.

Fig. 4 Observed FOD peaks in normal and robust MSMT. A distinct problem of normal MSMT is that it finds peaks in nearly all the voxels. This happens in voxels containing only isotropic diffusion because outlier slices mimic signal loss in DWIs. Consequently, the algorithm thinks that there is anisotropic diffusion in that direction therefore returning an artificial peak. On the contrary, in voxels containing true anisotropic diffusion in multiple directions (crossings), the artificial anisotropy due to outliers can hide these correct peaks due to general decrease in diffusivity.

Fig. 5.A sagittal slice of DWI volume affected by outliers pre and post motion correction visualizes how axial outlier slices can become oblique. SOLID weights are used to map the decreased reliability to voxel-wise weights. An average reliability calculated over all volumes in motion corrected DWI space is useful quality control tool. It shows quickly which spatial regions are affected by outliers. The reliability weights used in the modelling are obtained from each individual SOLID-reliability map (same dimensions with DWI volume) to utilize voxel-wise outlier information.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

3301

DOI: https://doi.org/10.58530/2022/3301