3294
Cumulant expansion with localization1Leeds Institute of Cardiovascular and Metabolic Medicine, University of Leeds, Leeds, United Kingdom, 2Cardiff University Brain Research Imaging Centre (CUBRIC), School of Psychology, Cardiff University, Cardiff, United Kingdom, 3LPI, ETSI Telecomunicación, Universidad de Valladolid, Valladolid, Spain, 4Leeds Institute of Cardiovascular and Metabolic Medicine, Leeds, United Kingdom, 5Division of Cardiovascular Medicine, Radcliffe Department of Medicine, University of Oxford, Oxford, United Kingdom, 6Department of Biomedical Engineering, Linköping University, Linköping, Sweden, 7Center for Medical Image Science and Visualization, Linköping University, Linköping, Sweden
Synopsis
Diffusion MR is sensitive to the microstructural features of a sample. Fine-scale characteristics can be probed by employing strong diffusion gradients while the small gradient regime is determined by the cumulants of the distribution of particle displacements. However, the cumulant expansion suffers from a finite convergence radius and cannot represent the ‘localization regime’ that emerges at higher gradient strengths characterized by a stretched exponential dependence. Here, we propose a new representation for the diffusion MR signal. Our method provides not only a robust estimate of the first few cumulants but also a meaningful extrapolation of the signal decay.
Introduction
Diffusion magnetic resonance imaging (dMRI) is a non-invasive tool to measure the diffusion of water molecules in a sample1-3. Small pore sizes can be revealed using high b-values. Small b-values, on the other hand, provide the cumulant expansion of the dMRI signal to its first terms3-5. However, the cumulant expansion has a finite convergence radius, and a new regime called localization regime emerges at higher gradient strengths characterized by the expression $$$-\ln{ \left( E \right)}\propto \left( bD_0 \right)^{1/3}$$$ 6-14. In this work, we provide an extension of cumulant expansion that can represent the diffusion-weighted signal in the localization regime as well.Methods
TheoryWe propose the following dMRI signal representation
$$E(q)=\exp\left(-(qr)^{2/3}\left((qu)^{\frac{4}{3}e^{-q^6p^6}}-(q v)^{\frac{10}{3}e^{-q^6p^6}}+(qw)^{\frac{16}{3}e^{-q^6 p^6}}\right)\right)\;\;\;\;\;\mathrm{(1)}$$
whose parameters are $$$r$$$, $$$u$$$, $$$v$$$, $$$w$$$, and $$$p$$$. The asymptotic (large-$$$q$$$) behaviour of this function is
$$E(q)=\exp\left(-(qr)^{2/3}+\mathcal{O}\left(q^{-4/3}\right)\right)\left((q u)^{\frac{4}{3} e^{-q^6p^6}}-(qv)^{\frac{10}{3}e^{-q^6p^6}}+(qw)^{\frac{16}{3} e^{-q^6 p^6}}\right) \label{eq:signal_high_q}$$
while at small $$$q$$$-values, it is given by
$$\ln{E}(q)=-q^2r^{2/3}u^{4/3}+q^4r^{2/3}v^{10/3}-q^6 r^{2/3} w^{16/3}+\mathcal{O}\left(q^8\right). $$
Clearly, $$$r$$$ determines the asymptotic behaviour. For a given $$$r$$$, $$$u$$$ determines the 2nd cumulant, $$$v$$$ determines the 4th cumulant and $$$w$$$ is related to higher order cumulants.
In this study, the representation in Eq. (1) is fitted to dMRI signals for two scenarios, namely, to orientationally-averaged signal15 and to single-direction acquisitions. In practice, it proved beneficial to fix $$$p=1\ \mu\mathrm{m}$$$ in the brain.
Experimental data from the previous studies9
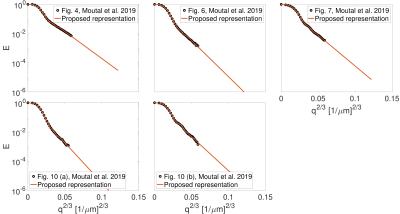
We used the experimental data from Figs. 4, 6, 7, 10 (a), and 10 (b) in9 which were acquired from physical phantoms with three different geometries; parallel plates, cylindrical tubes, and cylindrical rods on a square grid.
In vivo data
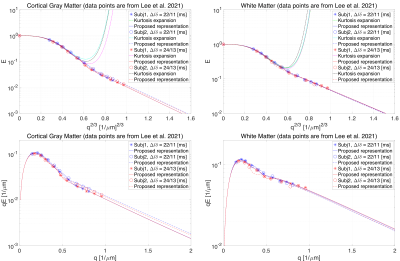
Two healthy participants were scanned using a 3T Connectom MR imaging system with a maximum gradient strength at $$$300\,\mathrm{mT}/\mathrm{m}$$$ (Siemens Healthineers, Erlangen, Germany). We used two acquisition protocols: 1) the first protocol comprised six $$$b=0$$$ and 11 non-zero shells at ($$$b = 0.4, \, 0.8, \, 1.2, \, 2, \, 3, \, 4, \, 6, \, 8, \,10,\,12,\,15 \; \mathrm{ms}/\mathrm{\mu}\mathrm{m}^2$$$) along $$$\left( 16, \, 16, \, 21, \, 31, \, 21, \, 21, \, 31, \, 31, \, 31, \, 31, \, 46 \right)$$$ gradient directions, respectively15,16 and 2) the second protocol includes the data acquired in a single direction, $$$(1/\sqrt{3}, \, 1/\sqrt{3}, \, 1/\sqrt{3})^\intercal$$$, following the same b-value distribution as the former one. Contrary to the former protocol, in the latter case, we repeated the measurements with the same number of directions per b-value as in the first protocol. In total, 66 axial slices were acquired with 2 mm isotropic voxel size, matrix size of 106$$$\times$$$106, TE/TR=55/4000 ms, $$$\Delta/\delta=23/12$$$ ms and partial Fourier factor of 6/8. The diffusion-weighted images were corrected for Rician bias17, Gibbs ringing artifacts18, eddy currents and subject motion using FSL EDDY19. We normalized the orientationally-averaged signal based on the $$$b = 0$$$ signal in each voxel. In this work, we have also used the data points from Fig. 3 in11.
Results
Fig. 1 shows the result of fitting the proposed representation to the experimental data from Fig. 4, 6, 7, 10 (a), and 10 (b) in Moutal et al.'s work9. The extrapolated signal follows the trend of localization regime ($$$-\ln{ \left( E \right)}\propto q^{2/3}$$$).The result of fitting the proposed representation to data from cortical gray matter and white matter voxels in11 is illustrated in Fig. 2. As it is shown, the representation based on the cumulant expansion (diffusion kurtosis imaging, DKI20) diverges at moderate q-values, while our representation fixes this problem.
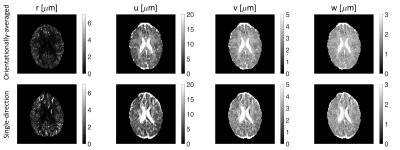
Fig. 3 shows the estimated parameters ($$$r$$$, $$$u$$$, $$$v$$$, $$$w$$$) of the representation for both orientationally-averaged and single-direction signals.
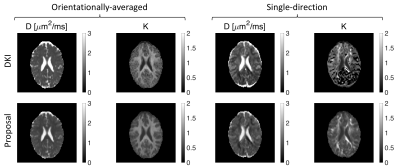
We extracted the apparent diffusion coefficient and kurtosis using DKI and the low-q approximation of our proposed representation. A good agreement between the maps from DKI and our proposed method is observed as illustrated in Fig. 4.
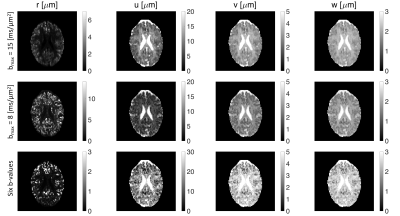
The effect of $$$b_\mathrm{max}$$$ and sampling of $$$b$$$-value on the estimated parameters ($$$r,u,v,w$$$) of the proposed representation is shown in Fig. 5. Reducing the maximum b-value to $$$b_{max}=8 ms/\mu m ^2$$$ does not change the maps considerably indicating the robustness of the representation while the change in the parameter maps is more significant if we use a subsample of six non-zero b-values ($$$b = 0, 0.8, 2, 4, 6, 10, 13 ms/\mu m^2$$$).
Discussion and conclusion
Our representation of the diffusion MR signal reproduces DKI at low gradient strengths while capturing the stretched exponential behavior consistent with the localization regime at large gradient strengths. We have thus achieved a meaningful extrapolation of the signal, overcoming a serious deficiency of DKI. Fitting a stretched exponential function to the entire diffusion-weighted signal profile is problematic as its low-q behavior suggests diverging moments for displacements21. Our representation has the stretched exponential tail, yet guarantees finite moments for the displacements. When one wants to take advantage of the localization regime, e.g., to estimate the soma size as in11, it is difficult to decide what range of b-values are to be used to fit the asymptotic form. Having a good representation would obviate this challenge. In conclusion, we introduced a new diffusion MRI signal representation that could perform well in the entire range of gradient strengths, and thus overcomes the well-known challenges associated with the commonly-employed representations.Acknowledgements
This project was financially supported by the Swedish Foundation for Strategic Research (RMX18-0056), Linköping University Center for Industrial Information Technology (CENIIT), LiU Cancer, Sweden's Innovation Agency (VINNOVA) ASSIST, and Analytic Imaging Diagnostic Arena (AIDA). This research was funded in whole, or in part, by a Wellcome Trust Investigator Award (219536/Z/19/Z, 096646/Z/11/Z) and a Wellcome Trust Strategic Award (104943/Z/14/Z). For the purpose of open access, the author has applied a CC BY public copyright licence to any Author Accepted Manuscript version arising from this submission. This work was also supported by the British Heart Foundation, UK (SI/14/1/30718), EPSRC (EP/M029778/1), and The Wolfson Foundation. Tomasz Pieciak acknowledges the Polish National Agency for Academic Exchange for the grant PN/BEK/2019/1/00421 under the Bekker programme and the Ministry of Science and Higher Education (Poland) under the scholarship for outstanding young scientists (692/STYP/13/2018).
References
1. Callaghan PT. Principles of nuclear magnetic resonance microscopy. Oxford University Press on Demand; 1993.
2. Price WS. NMR studies of translational motion: principles and applications. Cambridge University Press; 2009 Jul 30.
3. Grebenkov DS. NMR survey of reflected Brownian motion. Reviews of Modern Physics. 2007 Aug 17;79(3):1077.
4. Kiselev VG. Fundamentals of diffusion MRI physics. NMR in Biomedicine. 2017 Mar;30(3):e3602.
5. Frøhlich AF, Østergaard L, Kiselev VG. Effect of impermeable boundaries on diffusion-attenuated MR signal. Journal of Magnetic Resonance. 2006 Apr 1;179(2):223-33.
6. Stoller SD, Happer W, Dyson FJ. Transverse spin relaxation in inhomogeneous magnetic fields. Physical Review A. 1991 Dec 1;44(11):7459.
7. de Swiet TM, Sen PN. Decay of nuclear magnetization by bounded diffusion in a constant field gradient. The Journal of chemical physics. 1994 Apr 15;100(8):5597-604.
8. Hurlimann MD, Helmer KG, Deswiet TM, Sen PN. Spin echoes in a constant gradient and in the presence of simple restriction. Journal of Magnetic Resonance, Series A. 1995 Apr 1;113(2):260-4.
9. Moutal N, Demberg K, Grebenkov DS, Kuder TA. Localization regime in diffusion NMR: theory and experiments. Journal of Magnetic Resonance. 2019 Aug 1;305:162-74.
10. Williamson NH, Ravin R, Benjamini D, Merkle H, Falgairolle M, O'Donovan MJ, Blivis D, Ide D, Cai TX, Ghorashi NS, Bai R, Basser PJ. Magnetic resonance measurements of cellular and sub-cellular membrane structures in live and fixed neural tissue. Elife. 2019 Dec 12;8:e51101.
11. Lee HH, Fieremans E, Huang SY, Qiyuan T, Novikov DS. Localization regime of diffusion in human gray matter on a high-gradient MR system: Sensitivity to soma size. In International Society for Magnetic Resonance in Medicine Annual Meeting 2021.
12. Grebenkov DS. Diffusion MRI/NMR at high gradients: Challenges and perspectives. Microporous and Mesoporous Materials. 2018 Oct 1;269:79-82.
13. Grebenkov DS. Exploring diffusion across permeable barriers at high gradients. II. Localization regime. Journal of Magnetic Resonance. 2014 Nov 1;248:164-76.
14. Grebenkov DS, Helffer B, Henry R. The complex Airy operator on the line with a semipermeable barrier. SIAM Journal on Mathematical Analysis. 2017;49(3):1844-94.
15. Afzali M, Knutsson H, Özarslan E, Jones DK. Computing the orientational-average of diffusion-weighted MRI signals: A comparison of different techniques. Scientific Reports. 2021 Jul 12;11(1):1-6.
16. Knutsson H. Towards optimal sampling in diffusion MRI. In International Conference on Medical Image Computing and Computer-Assisted Intervention 2019 Oct 13 (pp. 3-18). Springer, Cham.
17. Koay CG, Özarslan E, Johnson KM, Meyerand ME. Sparse and optimal acquisition design for diffusion MRI and beyond. Medical physics. 2012 May;39(5):2499-511.
18. Kellner E, Dhital B, Kiselev VG, Reisert M. Gibbs‐ringing artifact removal based on local subvoxel‐shifts. Magnetic resonance in medicine. 2016 Nov;76(5):1574-81.
19. Andersson JL, Sotiropoulos SN. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage. 2016 Jan 15;125:1063-78.
20. Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional kurtosis imaging: the quantification of non‐gaussian water diffusion by means of magnetic resonance imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2005 Jun;53(6):1432-40.
21. Özarslan E, Shepherd TM, Koay CG, Blackband SJ, Basser PJ. Temporal scaling characteristics of diffusion as a new MRI contrast: findings in rat hippocampus. Neuroimage. 2012 Apr 2;60(2):1380-93.
Figures