Introduction

Multi-directional phase-contrast flow MRI in real time based on highly undersampled radial acquisitions¹ can provoke marked concomitant field contributions that vary for individual radial projections (spokes) and that impair quantitative velocity maps. Recently, a computationally expensive correction strategy has been proposed, that includes concomitant phase errors in a non-linear model-based image reconstruction on a spoke-by-spoke basis². Because the approach becomes impractical for large numbers of spokes, this work aims at reducing the numerical costs by proposing a clustering of phase errors in the spoke dimension.

Methods

Phase error maps by concomitant magnetic fields are characterized by Maxwell coefficients, which are determined by individual gradient design similar to³. In a pre-processing step, these coefficients are clustered in the spoke dimension using the k-means algorithm⁴ to reduce the total number of individual phase error maps. Thus, similar maps of different spokes are represented by their mean, which reduces the number of Fourier transforms required in the forward model of the model-based reconstruction with radial Maxwell correction².
$$ F_{j,l}: x \mapsto \sum_s^k P_{l,s} \text{ FT} \left\{ \rho \cdot \exp\left(i \phi_{l.s} \right) \cdot \exp\left( i\sum_d E_{l.d} v_d \right) \cdot c_j \right\} $$
Here, multiple velocity maps $$$v_d$$$ are jointly estimated along with the complex image $$$\rho$$$ and coil profiles $$$c_j$$$. Individual velocity encodings ($$$l$$$) are assumed to only differ in phase ($$$E_{l.d} v_d$$$) or by the individual Maxwell phase error map $$$\phi_{l.s}$$$, where $$$s$$$ is the index along the clustered spoke dimension. The number of Fourier transforms, clustered sampling patterns ($$$P_{l,s}$$$) and clustered phase error maps ($$$\phi_{l.s}$$$) are set in advance by the parameter $$$k$$$ – the argument of the k-means algorithm. Therefore, $$$k$$$ decides whether all individual Maxwell phase errors are compensated for on a spoke-by-spoke basis ($$$k = N_S$$$ the number of spokes per frame) or a compromise is chosen between reconstruction time and accuracy of velocity quantification ($$$k <N_S$$$). Reconstructions of real-time three-directional velocity maps¹ in the aortic arch were performed individually for the full range of $$$k$$$ and reconstruction times were recorded. RMSE values were evaluated in static image regions and served as indicator of velocity accuracy. MRI acquisition parameters were: B₀ = 3 T, Venc = 150 cm/s, TE/TR = 2.10/2.94 ms, FA = 10°, base resolution = 178, spokes per frame 5, resolution: 1.8 x 1.8 x 6 mm³, frame rate 17 fps, velocity directions 3.

Results

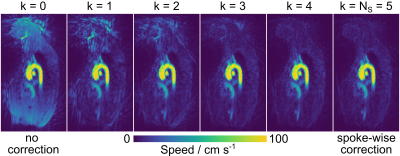
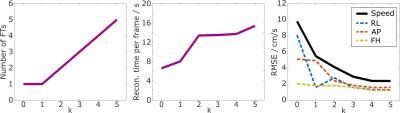
Figure 1 compares speed maps (velocity vector length) without Maxwell correction ($$$k=0$$$) and with Maxwell corrections using different numbers of phase-error clusters ($$$k = 1$$$ to $$$5$$$). For increasing $$$k$$$ the image quality visually improves as phase offset errors and image artifacts decrease. As shown in Figure 2 this observation is accompanied by a decaying RMSE in static regions, while the reconstruction time increases as a function of $$$k$$$.

Discussion

This work shows that clustering the Maxwell coefficients along the spoke dimension can be considered a tool to balance velocity accuracy and reconstruction time. The approach comes with a control parameter $$$k$$$ that allows to speed up the reconstruction in the case of small inter-spoke differences of concomitant phase errors, or alternatively, to focus on the velocity accuracy and fully compensate for individual phase errors on a spoke-by-spoke basis. The only disadvantage is, that $$$k$$$ has to be set in advance, i.e. prior to the image reconstruction. Given a fixed radial phase-contrast protocol, however, the best choice of $$$k$$$ can be fixed too. For the given example with large inter-spoke differences of Maxwell terms and only 5 spokes per frame, $$$k=4$$$ seems to best balance velocity accuracy and reconstruction time. More examples are warranted to better assess the performance of the approach. Especially for acquisitions with larger numbers of spokes, the clustering of Maxwell terms is expected to be of great benefit, as otherwise the reconstruction time scales with the number of spokes. With potentially reduced reconstruction times, the clustering-approach might even be a prerequisite for a practical radial Maxwell correction addressing inter-spoke differences.

Conclusion

For undersampled radial phase-contrast acquisitions, a clustering of Maxwell terms in the spoke dimension can reduce image reconstruction times of a model-based image reconstruction, while simultaneously compensating for inter-spoke differences of concomitant phase errors in quantitative velocity maps.