INTRODUCTION

It is known mechanical properties of brain tissues are important to understand its disease and development¹. Ex vivo studies have also shown a strong bond between mechanical and structural properties of brain tissues^{2, 3}. Using magnetic resonance elastography (MRE)⁴ and diffusion weighted imaging (DWI)⁵, mechanical and structural properties of soft tissues could be measured in vivo⁶. However, the potential relationship between mechanical and structural properties of brain is yet to be explored.

In this study, we used DWI and MRE to characterize the potential correlation between structural and biomechanical properties of brain. Apparent diffusion coefficient (ADC) and shifted ADC (sADC) values were estimated. The correlations between sADC and shear modulus were analyzed for each of the specific brain region at 3 different actuation frequencies. A phenomenological model based on sADC and the shear modulus was proposed.

METHODS

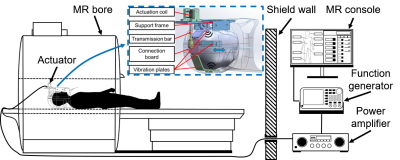
A total of 43 healthy volunteers were recruited in this study. Among all the subjects, data from the 32 subjects were used for modeling and the rest 11 subject data were used for validation. MRE imaging was performed using a custom-built electromagnetic actuator⁷ (Figure 1). The measurement was carried out using 4 actuation frequencies. Among them, data from 20, 40, 60 Hz were used for correlation analysis. Data from 30 Hz were used for validation. Wave images of the brain were acquired using an echo planar imaging (EPI) based MRE sequence with three motion encoding directions. Shear modulus maps were calculated by using a three-dimensional local frequency estimation (LFE) method. For DWI, images were acquired with diffusion encoding along three axes. Among the 16 key b-values between 0 and 2500 s/mm² acquired, we selected 2 optimized key b-values to calculate sADC as the following equation, so that Gaussian and non-Gaussian diffusion effect was included.
$$sADC=ln(S_{lb}/S_{hb})/(hb-lb)$$
where $$$S_{lb}$$$ and $$$S_{hb}$$$ are intensities of the signals acquired at the low and high key b-value, $$$lb$$$ and $$$hb$$$, respectively. Both MRE and DWI scanning were performed on a 3T MR imager (uMR 790, United Imaging Healthcare, Shanghai, China).

All MRE and DWI images were registered to a common reference (MNI152 T1-weighted 2 mm brain atlas) by using Advanced Normalization Tools (ANTS) for segmentation and correlation analysis. The whole brain was segmented into frontal, occipital, parietal, and temporal lobe using the MNI template mask within the FMRIB Software Library (FSL).

Correlations between shear modulus and sADC results were evaluated using Pearson correlation coefficient. The linear correlation coefficient was quantified voxel by voxel at each frequency. All p values were corrected by the false discovery rate (FDR) method. A linear regression between the mean value of shear modulus and sADC were performed in each lobe. We proposed the following equation for the frequency-dependent shear modulus, $$$μ_{f}$$$, at each vibration frequency, $$$f$$$, in terms of :
$$μ_{f}=(α_{1}f^{β_{1}}+γ_{1})\cdot sADC+(α_{2}f^{β_{2}}+γ_{2})$$
where $$$α_{i}$$$, $$$β_{i}$$$, and $$$γ_{i}$$$ are the model parameters to be determined by fitting.

RESULTS and DISCUSSION

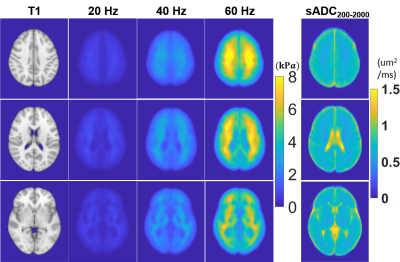
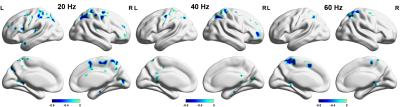
Based on the highest correlation between the shear modulus and sADC at each frequency, we determined the 2 key b-vlaues as 200 s/mm² and 2000 s/mm². T1-weighted images, average shear modulus, and average sADC values over the 32 subjects are shown in Figure 2. We observed the anatomical features of the brain such as white matter and ventricle regions could be identified base on the modulus and sADC maps.

Voxel correlation results along 3 equally spaced frequencies are shown in Figure 3. The voxels with significant correlation had been shown illustrated. For all 3 actuation frequencies, large amount of contiguous significant voxels were observed only in parietal lobe.

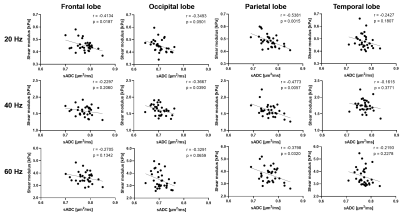
The results from linear regression study confirmed the specificity of parietal lobe found in voxel correlation maps in Figure 3. Significant linear correlation was observed for all 3 frequencies in parietal lobe. However, significant correlations were observed for frontal and occipital lobes at 20 and 40 Hz. As for the temporal lobe, there was no significant correlation at any of the measured frequency.

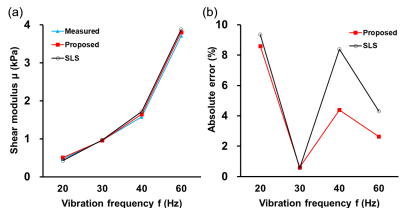
The predicted mean values from the proposed model and the standard linear solid (SLS) model of the 11 validation subjects are shown in Figure 5(a). For absolute error comparing with the measured results, the proposed model outperforms SLS model at 20, 40 and 60 Hz (Figure 5b). Especially for 40 Hz and 60 Hz, around 50% error decrease could be achieved by using the proposed model. These indicated the proposed model had better performance at high frequencies.

CONCLUSION

In this study, we proposed a phenomenological model for parietal lobe to describe the shear modulus by sADC at multiple frequencies. The validation results highlighted the utility of the empirical model compared with the classic spring-dashpot models. These results also demonstrated a strong correlation between mechanical properties and structural properties in parietal lobe.

Acknowledgements

Funding support from grant 31870941 from National Natural Science Foundation of China (NSFC) and grant 19441907700 from Shanghai Science and Technology Committee (STCSM) are acknowledged.