Introduction

There is a relation between diseases and functional disorders and the stiffness of biological tissues. It is known that lesions such as tumors and hepatic fibrosis are stiffer than normal tissues, and quantitative measurement of the viscoelastic modulus of biological tissues is considered to be effective in diagnosis. MRE is a non-invasive method for quantitative measurement of the viscoelasticity of tissues using MRI, which can estimate the elastic modulus distribution by applying vibration from the body surface using an external driver, imaging the propagation of the elastic waves in the target region, and solving the inverse problem. LFE, DI, and MMDI have been proposed as the elastic modulus estimation method, but there is a trade-off between quantitativeness and spatial resolution. In this study, we developed an elastic modulus estimation method using deep learning and evaluated the quantitative performance, spatial resolution, and noise robustness of the proposed method using numerical simulations.

Method

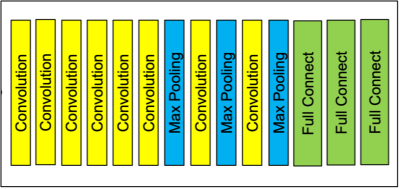
The learning model developed in this study is shown in Figure 1. We added noise (0~0.20 in increments of 0.05) to the elastic wave images created by the elastic wave simulator and trained the learning model with it. In order to evaluate the robustness to noise and quantitativeness of the model, we first used plane-wave elastic wave images for plane-wave propagation angles (π/8, π/4, 3π/8) and amplitude to noise ratio (ANR) (amplitude 2 rad, noise standard deviation 0~0.2 in 0.05 increments). In order to increase the spatial resolution of the proposed method, we changed the method to use U-Net to determine the size of the segmented pixels, as shown in Figure 2. Then, the edge reproducibility of the proposed method was evaluated by applying to an elastic wave image with an ANR of 20 propagating through a two-layered object with 3 kPa at the top and 8 kPa at the bottom. The vibration frequency was 62.5 Hz, the loss function was a sum-of-squares error in CNN-Model, cross-entropy in U-Net, the optimization algorithm was Adam, and the number of training data was 3,000.

Results

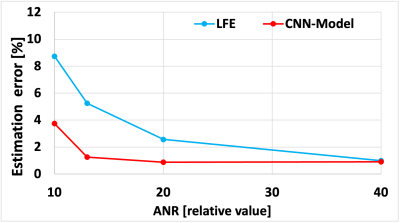
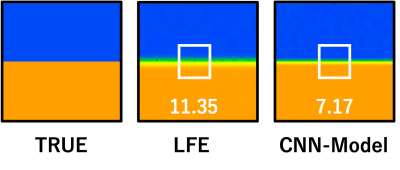
As shown in Figure 3, when the elasticity is high (8 kPa) and the ANR is low (10), the LFE produces an estimation error of up to 10.8%, whereas the proposed method produces an error of up to 4.3%. In terms of edge reproducibility, the RSME in a 10×10 pixel region, including the boundary region, was 11.35 for the LFE, while 7.17 for the proposed method (Figure 4).

Discussion

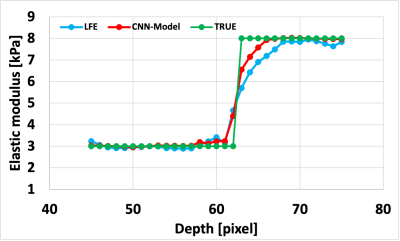
It is suggested that the estimation method based on deep learning is independent of the propagation angle of plane waves and has higher estimation accuracy than LFE, especially for high elastic moduli. By learning various propagation patterns of elastic waves, high quantitativeness could be maintained even when the ANR is low or the wavelength is long. Although the reproducibility of the edge was better than that of LFE (Figure 5), it is necessary to investigate the case where the difference in elastic modulus between the two regions is different.

Conclusion

We developed a method for estimating the elastic modulus using deep learning and evaluated its quantitativeness, spatial resolution, and noise robustness through numerical simulations. It suggests that the method has the same level of noise robustness as LFE, higher spatial resolution, and higher quantitativeness for higher elastic modulus.

Acknowledgements

This study was supported by MEXT and JSPS Grants-in-Aid for Scientific Research on Innovative Areas (grant nos. JP17H02115 and JP17H05279).