Introduction

Shear modulus eastimation is crucial for MR elastography (MRE)¹. Conventional algorithms based on the Navier-Stokes equation provide several strategies for modulus estimation, including direct inversion (DI), local frequency estimation (LFE), and nonlinear inversion (NLI)². Recent studies showed deep learning-based methods trained on simulated data could provide higher robustness and time-efficiency for modulus estimation^3,4. In addition, it is shown that LFE algorithm combined with a neural network outperformed the conventional significantly⁵. In this study, we propose a neural network based on physics models, aiming to achieve higher precision of modulus estimation and boundaries identification.

Methods

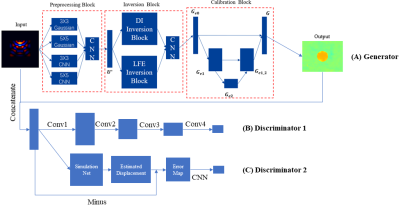
The proposed network is based on a GAN structure, consisting of a DI and LFE-based generator, a general discriminator, and an NLI-based discriminator (Figure 1). For the generator, three blocks with different structures are established, which are designed for preprocessing, inversion and postprocessing respectively. In the preprocessing block, convolution layers with different filter sizes and initial weights are set up and coalesced by the following CNN structure. In the inversion block, DI and LFE algorithms are applied to achieve the domain transformation from wave images to stiffness maps, respectively. The results are then merged by a CNN structure. To calibrate the fused modulus map, a Unet-based structure is applied in the last stage. The errors of modulus estimation and boundaries identification are corrected in this block. Finally, the loss function for the training of the generator is described as:
$$Loss_G =\min_{\theta_0}{ {\left \| f_G(U_{acq},\theta_0) - G_{label} \right \|}_1 }$$
where $$$U_{acq}$$$ is the acquired wave image as network input, $$$G_{label}$$$ is the reference shear modulus map. $$$f_G(\cdot)$$$ denotes the output of the proposed generator, while $$$\theta_0$$$ is the trainable parameters of the generator.
In addition, two discriminators are applied to improve the calculation accuracy. The first one is a conventional discriminator adopted from the pix2pix model, which enhances details in stiffness maps⁶. In the second discriminator, the simulation network is a pretrained model which estimates a wave image from a stiffness map based on the Helmholtz equation and a Unet-based structure. The difference between the estimated and acquired wave images indicating calculation errors of the generator is minimized. The discriminators are trained by optimizing the following loss functions:
$$Loss_D = Loss_{D1}+Loss_{D2}$$
$$Loss_{D1} = \min_{G_{est},\theta_1}{ {\left \| f_{D1}(G_{est},\theta_1) - \mathbf{M} _{fake} \right \|}_2^2 + {\left \| f_{D1}(G_{label},\theta_1) - \mathbf{M} _{real} \right \|}_2^2}$$
$$Loss_{D2} = \min_{G_{est}}{ {\left \| f_{D2}(G_{est}) - U_{acq} \right \|}_2^2}$$
where $$$\mathbf{M} _{fake}$$$ and $$$\mathbf{M} _{real}$$$ are matrices with single element 0 or 1, respectively. $$$G_{est}$$$ is the stiffness map estimated by the generator. $$$f_{D1}(\cdot)$$$ and $$$f_{D2}(\cdot)$$$ denotes the results of two discriminators.
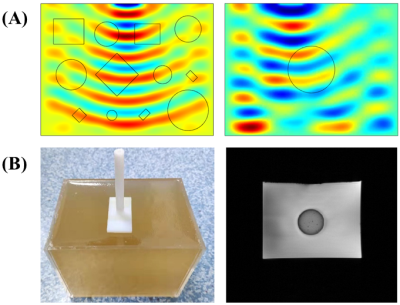
Over 5000 wave images were simulated by COMSOL as the training dataset, while MRE data of a gel phantom with a stiffer inclusion was acquired with a 40/60Hz vibration (Figure 2). For comparison, a pix2pix model was also trained with the prepared dataset to evaluate the generalization capability of the proposed method.

Results and Discussion

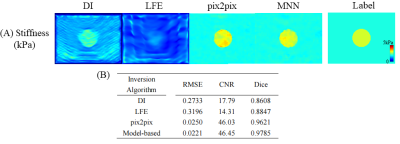
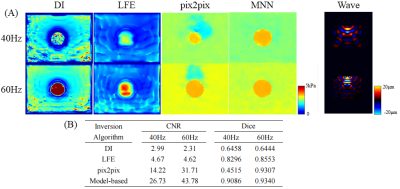
Results from MNN outperformed that from DI and LFE . The boundary of the inclusion was relatively sharp with the pix2pix model or the proposed method, while noticeable artifacts covered the target in the results of DI and LFE (Figure 3A). In addition, the RMSE decreased to 0.025 by over 90%, while the CNR rose up to 46 by 3 times (Figure 3B). Compared with DI and LFE, the Dice coefficient of MNN was 10% higher . (Figure 3B). The results indicated that the deep learning-based methods provided higher estimation accuracy and better boundary identification.
In the experiment of acquired wave images, the results demonstrated the limitation of the data-driven model (pix2pix). Nonnegligible artifacts appeared and the wrong size of the inclusion was estimated (Figure 4A). In contrast, the proposed method showed better generalization ability. The CNR coefficient of MNN achieved an over 30% increase, while the Dice coefficient kept a high level for all test conditions (Figure 4B). Since the stiffness estimation was accomplished by DI and LFE layers, we observed a better generalization of MNN.

Conclusion

In this study, we proposed a physics model-based neural network for modulus estimation. DI and LFE algorithms were encapsulated as layers transforming wave images to shear modulus maps. We were able to achieve improved estimation accuracy with enhanced generalization capability. Results showed the potential of MNN in a variety of MRE applications.

Acknowledgements

Funding support from grant 31870941 from National Natural Science Foundation of China (NSFC) and grant 19441907700 from Shanghai Science and Technology Committee (STCSM) are acknowledged.