Introduction

Cortical surface-based analysis is widely used in pediatric neuroimaging studies to better quantify the rapidly developing brain and detect brain disorders. As the neuroimaging field increasingly moves to large-scale studies, quality assessment (QA) becomes a crucial step in identifying and excluding reconstructed low-quality cortical surfaces due to extremely low image contract and severe motion effects, which would otherwise lead to inaccurate analysis. Convolutional Neural Networks (CNNs) have demonstrated superior performance in image QA ¹, but they are inapplicable for the complex and convoluted cortical surfaces, which are represented with triangle meshes sitting in a manifold space and have an intrinsic spherical topology. To address this issue, inspired by the attention mechanism ², we unprecedentedly propose a spherical transformer layer as a substitute to the convolution operation in CNNs for cortical surface QA. It is a content-based vertices interaction mechanism, which aggregates information from vertices in the local surface patches based on their feature correspondences rather than the relative positions, thus enabling itself to be directly applied to the spherical surface structure and describe the local structural and contextual patterns properly. Our proposed surface network with spherical transformer layers demonstrates superior performance on quality assessment of 1,860 pediatric cortical surfaces.

Materials and Methods

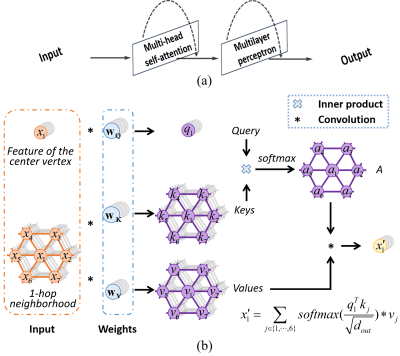
In this study, we processed an infant brain MRI dataset with 1,860 scans. Cortical surface were reconstructed using the public infant dedicated MRI computational pipeline: iBEAT V2.0 Cloud ³. Reconstructed cortical surfaces were further mapped onto a sphere and aligned onto the age-matched templates in UNC 4D infant cortical surface atlases ⁴. Then, all spherical surfaces were resampled with the same tessellation with 163,842 vertices for the spherical convolution operations. For each vertex on the surface meshes, 3 features were computed to describe their local geometry and morphometry, i.e., the mean curvature, sulcal depth, and cortical thickness, which were normalized into [0, 1] before being fed into our model. The quality of each cortical surface was assessed by experienced experts as the ground truth.
To effectively distinguish the problematic surfaces from the good ones, we propose a spherical transformer layer to describe the local structural and contextual patterns on the spherical manifold, which begins with the self-attention operation as shown in Fig. 1 (b). The self-attention operation is essentially an aggregation function, which weightedly sums the feature representations from vertices in a local surface patch and assigns the product to the center vertex. Specifically, given a vertex on the spherical surface, we first define its one-hop neighborhood and extract its query vector and the key and value vectors for its neighbors by linear transformations. To evaluate the feature correspondences among the center vertex with its neighbors, we conduct the inner product between the query and keys, which produces a correlation matrix A as the weight in the aggregation function. Then, by multiplying A with the value vectors, the geometrical and morphometric features in the local patch are concluded and assigned to the center vertex, which is equivalent to the convolution operation in CNNs. To promote the diversity of the content-based correlation A, multi-head self-attention is implemented in a multi-branch structure and fused with a fully connected layer. A multilayer perceptron is further proposed for feature transformation and constituting a spherical transformer layer together with the multi-head self-attention as illustrated in Fig. 1 (a).
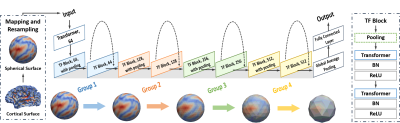
With our spherical transformer layers extracting features on the spherical surface, we propose a spherical ResNet-based architecture ⁵ as shown in Fig. 2. A transformer (TF) block is built, consisting of two transformer layers followed by two batch-normalization and ReLU functions. At the final layer, global average pooling is applied together with a fully connected layer to compute the confidence scores in two classes corresponding to Fail and Pass. As we typically have more Pass samples than Fail samples, the focal loss ⁶ is adopted as the objective function to deal with the data imbalance problem.

Results

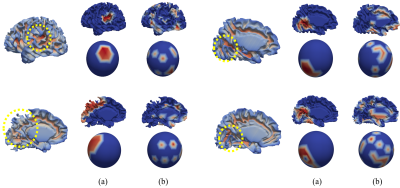
Three performance metrics are adopted for validating our method, including F1-score (F1), precision (PRE), and recall (REC), which are respectively defined as F1=(PRE+REC)/2, PRE=TP/(TP+FP), and REC=TP/(TP+FN). Herein, TP, FP, and FN are abbreviations for the number of true positive, false positive, false negative cases, respectively. Our method achieved superior performance against a recently published convolution-based spherical network method SphereConv ⁷, i.e., PRE=87.63%, REC=85.00%, and F1=86.29%, while SphereConv obtained PRE=83.33%, REC=82.50% and F1=82.91% with comparable parameters. To help us better understand the capability of the proposed method, Fig. 3 demonstrates several feature maps learned by our spherical transformer and SphereConv with Grad-Cam ⁸. It can be observed that our spherical transformer layer properly focuses on the structural artifacts around the problematic cortical regions, leading to better interpretabilities.

Conclusions

We proposed a spherical transformer-based network for quality assessment of pediatric cortical surfaces. It differs from the previous CNN-based methods due to its content-based feature aggregation function and can be applied onto the spherical surface manifold directly to effectively extract the local contextual and structural features for quality assessment of brain cortical surfaces. By testing on 1,860 infant cortical surfaces, we validated its superior performance in capability against convolution-based methods and demonstrated its strong interpretability.

Acknowledgements

This work was partially supported by NIH grants (MH116225 and MH123202 to G.L., MH117943 to L.W. and G. L., MH109773 to L.W.).