3169
Motion correction using Pilot Tone: a general model-based approach
YAN TU HUANG1, Peter Speier2, Tom Hilbert3,4,5, and Tobias Kober3,4,5
1Magnetic Resonance, Siemens Shenzhen Magnetic Resonance Ltd., Shenzhen, China, 2Magnetic Resonance, Siemens Healthcare, Erlangen, Germany, 3Advanced Clinical Imaging Technology, Siemens Healthcare, Lausanne, Switzerland, 4Department of Radiology, Lausanne University Hospital and University of Lausanne, Lausanne, Switzerland, 5LTS5, École Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
1Magnetic Resonance, Siemens Shenzhen Magnetic Resonance Ltd., Shenzhen, China, 2Magnetic Resonance, Siemens Healthcare, Erlangen, Germany, 3Advanced Clinical Imaging Technology, Siemens Healthcare, Lausanne, Switzerland, 4Department of Radiology, Lausanne University Hospital and University of Lausanne, Lausanne, Switzerland, 5LTS5, École Polytechnique Fédérale de Lausanne (EPFL), Lausanne, Switzerland
Synopsis
Motion continues to be a major impediment in clinical MRI. Using Pilot Tone to correct for motion is highly attractive as it uses inexpensive hardware and is independent from sequence. Here, we propose a model-based approach to calculate motion parameters from Pilot Tone signal. To avoid non-convergence those models are prone to, we introduce predefined displacement fields with the Pilot Tone as auxiliary, resulting in a linear motion model with fewer unknowns. Validation is performed on numerically simulated data and in-vivo measurements, comparing different motion models. Image reconstructions with the Pilot Tone showed fewer residual motion artefacts and converged faster.
Introduction
Motion continues to be a major impediment in clinical MRI and motion correction is an ongoing field of research. Retrospective model-based motion correction typically solves image and motion parameters iteratively1,2 by repeating two steps. The first step is solving for image x as a linear inverse problem:$$y=AFSTx$$
Here y is actual measured k-space data, T the motion transformation, S the coil sensitivity maps, F the FFT operator, and A the sampling mask. The second step is solving for motion parameters: either for rigid motion as a nonlinear inverse problem (e.g., AlignedSens)1, or for nonrigid motion as linear inverse problem with a large number of unknowns and with external signals (e.g., GRICS)2. Recently, Pilot Tone (PT) has been used to detect respiratory3, cardiac4 and head motion5,6. Using PT to correct for motion is highly attractive as it can be measured independently from the sequence with inexpensive hardware. Here, we propose a method which exploits the motion information contained in the PT signal to improve iterative model-based motion correction for both rigid and nonrigid motion; we test this concept in a Turbo Spin-Echo (TSE) acquisition.
Methods
First, we calculate the difference between y and estimated k-space data $$$AFST\widehat{x}$$$:$$r=y - AFST\widehat{x} $$
Here $$$\widehat{x}$$$ is the current image estimate, solution from first step in current iteration. The motion parameters $$$a$$$ can then be calculated by solving the linear inverse problem:
$$r=AFSGDa$$
with
$$G=-z$$
Here z is the gradient of motion-transformed images of all time segments (i.e., shots of the TSE acquisition). D is predefined displacement fields. Here, we use 2D rigid motion which contains translations and rotations (see Figure 1) and 2D affine motion which contains translations, shearing and optionally scaling operations. D can be extended to 3D motion and complex nonrigid motion which can be approximated by a combination of a small number of predefined displacement fields.
Assuming that the PT signal is linearly correlated to the motion parameters, a forward model can be formulated6:
$$a=Pm$$
with P being the PT signal, and m a vector of linear relationships. We can now have
$$r=AFSGDPm$$
By solving this linear inverse problem, we determine m. With m, we calculate the current motion state for constructing T for the first step in next iteration. This process is then repeated for a fixed number of iterations, whereas in each iteration, the relative error of y is calculated by:
$$RelErrY = ||r||/||y||$$
Numerical Simulations
We extended the MATLAB implementation of AlignedSens from Ref.1 by the method described above. We then generated a multi-shots Cartesian 2D dataset, motion was pure in-plane rotation with a uniform random distribution between shots. PT signal was approximated by summing each coil’s complex image at each shot (which gives an FID navigator-like signal7). We simulated 16, 32, 64, 128 shots and a maximum rotation of 10, 20 degrees to evaluate the method’s performance compared to AlignedSens. All processing was performed using MATLAB (MathWorks, USA) on an Intel i7-9750H CPU.
In-Vivo Measurement
A volunteer test was performed at 1.5 T (MAGNETOM Amira a BioMatrix system, Siemens Healthcare, Erlangen, Germany). A 13-channel body-flex coil of the vendor with a built-in PT generator was used instead of the head coil’s anterior part. Two T2w TSE datasets were acquired (matrix size 357*512, 17 shots, echo train duration 250ms, TR 4.7s, slice thickness 5mm). For the first measurement, the volunteer was asked to stay still to have a motionless reference image. During the second measurement, the volunteer performed small head rotations. As the rotations may be through-plane, we used an affine motion model without scaling. Processing was performed with a C++ implementation using Armadillo on Intel i7-9750H employing a multi-resolution approach (starting at 1/3 of the base resolution).
Results and Discussion
In the numerical simulations, our proposed method is faster and shows better convergence for a high number of shots and larger rotation angles; this further improves when we included simulated PT signal. Figure 2 shows the comparison between the ground truth and motion-corrected image - the reconstruction error $$$|\widehat{x}-x|/max(|x|)$$$ is very small (~2%), as well as convergence of the different algorithms: with PT > without PT > AlignedSens. Figure 3 shows the convergence of the algorithms depending on the number of shots and severeness of motion. For large values (10 degrees and shots > 64, 20 degrees and shots = 64) the correction required the PT to converge. In-vivo , within almost the same reconstruction time less than 40s, motion correction with PT results in better image quality and better convergence than without PT (see Figure 4). However, the improvement is smaller than in the numerical simulation. The reason might be that the PT signal was of limited quality (Figure 5a) and showed high noise even without motion (Figure 5b), probably caused by using a body-flex coil for imaging the head.Conclusion
Our initial results demonstrate good performance of our proposed method and potential practical rigid/affine motion correction within acceptable reconstruction time. Turning the motion estimation into a linear problem and reducing the number of unknown parameters improves the performance. Future work will be on 3D rigid, complex nonrigid motion correction with this method.Acknowledgements
No acknowledgement found.References
- Cordero-Grande L, Teixeira RPAG, Hughes EJ, Hutter J, Price AN, Hajnal J V. Sensitivity Encoding for Aligned Multishot Magnetic Resonance Reconstruction. IEEE Trans Comput Imaging. 2016;2(3):266-280. doi:10.1109/tci.2016.2557069
- Odille F, Vuissoz PA, Marie PY, Felblinger J. Generalized reconstruction by inversion of coupled systems (GRICS) applied to free-breathing MRI. Magn Reson Med. 2008;60(1):146-157. doi:10.1002/mrm.21623
- Vahle T, Bacher M, Rigie D, et al. Respiratory Motion Detection and Correction for MR Using the Pilot Tone: Applications for MR and Simultaneous PET/MR Examinations. Invest Radiol. 2020;55(3):153-159. doi:10.1097/RLI.0000000000000619
- Bacher M. Cardiac Triggering Based on Locally Generated Pilot-Tones in a Commercial MRI Scanner: A Feasibility Study. Published online 2017.
- Speier P, Bacher M, Bollenbeck J, Fenchel M, Kober T. Separation And Quantification Of Head Motion Modes By Pilot Tone Measurements. In: Proc. Intl. Soc. Mag. Reson. Med. 26(2018).
- Wilkinson T, Godinez F, Brackenier Y, et al. Motion Estimation for Brain Imaging at Ultra-High Field Using Pilot-Tone: Comparison with DISORDER Motion Compensation. In: Proc. Intl. Soc. Mag. Reson. Med. 29(2021).
- Wallace TE, Afacan O, Waszak M, Kober T, Warfield SK. Head motion measurement and correction using FID navigators. Magn Reson Med. 2019;81(1):258-274. doi:10.1002/mrm.27381
Figures

Figure 1: Example of 2D rigid motion predefined
displacement fields.
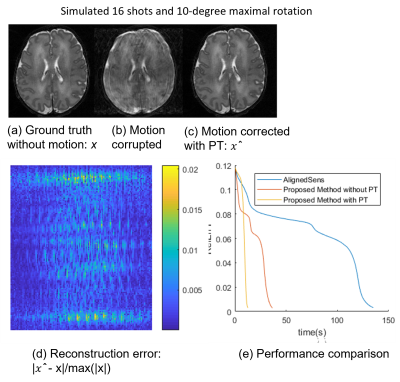
Figure 2: Result of 16
shots and maximal 10-degree rotational motion: (c) Motion corrected with PT. (d) Image reconstruction
error with PT and in scaled colors (maximum ~2%). (e) Convergence: with PT > without PT > AlignedSens.
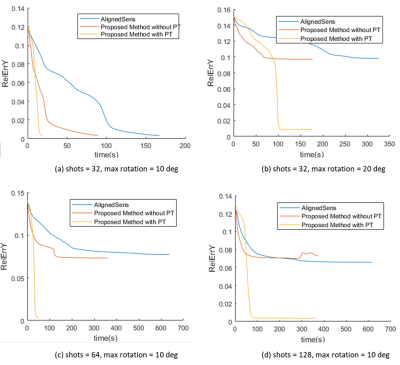
Figure 3: Results
for increased shots and larger maximal rotation angle. For large values (10
degrees and shots > 64, 20 degrees and shots = 64) the correction required
the PT to converge.
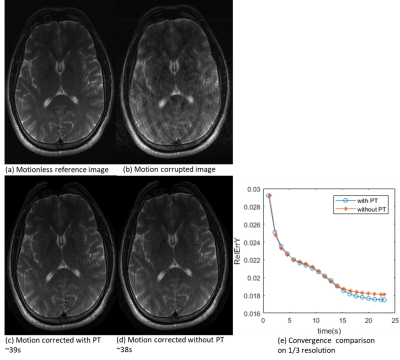
Figure 4: Motion corrected image (c) with PT (39s
reconstruction time) which has less motion artifact than (d) without PT (38s
reconstruction time). (e) The algorithm with PT has better convergence.
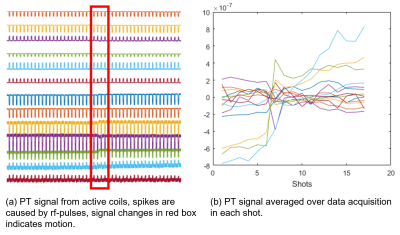
Figure 5: Measured PT signal with (a) changes due to
motion in the red box. Changes are small and only slightly higher than the
noise level. (b) Averaged PT signal over data acquisition for each shot, it has high
noise even in the no motion period.
DOI: https://doi.org/10.58530/2022/3169