3041
Non-local low rank denoising method for complex-valued DWI
Xinyu Ye1, Xiaodong Ma2, Ziyi Pan1, Steen Moller2, Eddie Auerbach2, Kamil Ugurbil2, Xiaoping Wu2, and Hua Guo1
1Center for Biomedical Imaging Research, Department of Biomedical Engineering, School of Medicine, Tsinghua University, Beijing, China, 2Center for Magnetic Resonance Research, Radiology, Medical School, University of Minnesota, Minneapolis, MN, United States
1Center for Biomedical Imaging Research, Department of Biomedical Engineering, School of Medicine, Tsinghua University, Beijing, China, 2Center for Magnetic Resonance Research, Radiology, Medical School, University of Minnesota, Minneapolis, MN, United States
Synopsis
Diffusion-weighted MRI (DWI) suffers from the intrinsic low SNR, especially for high-resolution and/or high b-value acquisitions. Thus, denoising methods are critical for diffusion images. Recently, increasing attention has been paid to complex DWI image denoising. Here, we propose a 2-step non-local low-rank joint denoising method to process complex-valued DWI images. Simulation data and in-vivo brain data were used to test the proposed method. The results showed that the proposed method may further improve the image quality.
Introduction
Diffusion-weighted MRI (DWI) provides valuable information for neuroscience study and disease diagnosis1. However, the decreased SNR caused by the diffusion weighting gradients hinders the acquisition of high-resolution DWI images. Many efforts have been made to develop denoising methods by exploiting the intrinsic redundancy of DWI signals2-4. Among these works, redundancy for local patches has been studied for denoising and is widely used5-7. Denoising methods on complex-valued data have also been proposed8 . Currently MPPCA based on local low-rank is widely used for DWI denoising7. With that, also inspired by another non-local low-rank denoising work9, we propose a 2-step non-local low-rank denoising method to process complex-valued DWI images.Theory
Two-step non-local low-rank denoising methodDWI images share structural similarities among different directions. Non-local methods can further improve the low-rankness by searching similar spatial patches with patch size 4. We implement a 2-step denoising method. The first step is to extract 3D patches across diffusion directions and then search non-local patches that are similar to each other. For this search, the noisy images are denoised using MPPCA first. Based on the Euclidian distance calculated from corresponding MPPCA-denoised patches, K=140 nearest patches are selected for each noisy patch. The second step is to denoise the noisy images based on the Casorati matrix formed by the selected non-local patches. For this, the singular value shrinkage is used to estimate the low-rank components.
Methods
Simulation datasetData from Fiberfox10 and HCP11 were used for simulation. For Fiberfox dataset, the noise-free and artifact-free images were created by simulating diffusion signals across a 3D brain-like phantom using Fiberfox. Single-shell b1k noise-free data with 34 diffusion directions were used and the matrix size was 108×90×90. For the HCP dataset, the reference images were generated using a DTI model12. Then we extracted 6 b0 and 30 b1k images from the generated reference images. The matrix size was 145×174×145. For both datasets, constant phase (=0) was added to generate complex images. 3D spatially variant noise with the characteristic of fast variations in x, and slow in y and z was added to the reference images13. Different noise levels were applied to test the performance.
In vivo dataset
We collected human brain images on a 7T MR scanner (Siemens, Erlangen, Germany), equipped with a body gradient (70 mT/m maximum strength and 200 T/m/s maximum slew rate). A healthy subject who signed a consent form approved by the local Institutional Review Board was scanned using the commercially available Nova 32-channel receive coil (Nova Medical Inc., MA).
We acquired slice-accelerated whole-brain DWI at 0.7-mm isotropic resolutions and with double-shell q-space sampling (b = 1k and 2k s/mm2). Relevant imaging parameters were: 2-fold slice acceleration and 3-fold in-plane acceleration, 6/8 partial Fourier, and TR/TE = 13370/91 ms. The data consisted of a total of 53 image volumes each obtained twice with opposed phase encoding. FLEET ACS 14 was utilized to minimize residual aliasing in final reconstructed images. Diffusion images of individual receive channels were reconstructed using the split-slice-GRAPPA algorithm 15 and were combined to form the final image via the SENSE combination method 16.
Using each dataset, we compared our method to existing methods including MPPCA and conventional non-local low-rank approach in which the patch searching was based on noisy images.
Result
For Fiberfox simulation data, the use of our method substantially improved the image quality (Fig. 1), outperforming MPPCA or conventional non-local low-rank approach, especially for higher noise levels. Quantitatively, it increased PSNR by up to 34.9% relative to the noisy images, by 3.7% relative to MPPCA and by 2.1% relative to the conventional non-local approach at noise level 10. The proposed method also provides higher SSIM.Likewise, the use of our method largely improved image quality (Fig. 2) for the HCP simulation data, increasing PSNR by 16.8% relative to the noisy images, by 1.1% relative to MPPCA and by 0.6% relative to the conventional non-local approach at a moderate noise level 4. SSIM is also increased by the proposed method.
Correspondingly, the improvement in image quality translated into improvement in the color-coded fractional anisotropy (cFA) (Fig. 3) as obtained from FMRIB Software Library(fsl)17.
In agreement with the simulation, the use of our method substantially improved the image quality for the 0.7 mm in-vivo data (Fig. 4), outperforming both MPPCA and conventional non-local approach in terms of restoring gray white matter contrast. Accordingly, the use of our method led to a cFA map (Fig. 5) that best delineated brain structure with least noise levels.
Conclusion
We proposed a 2-step non-local low-rank denoising method to jointly denoise complex-valued DWI images. Using both simulation and in-vivo data, we demonstrated that the proposed method can suppress noise while preserving the fine structures and provide better denoising performances than existing methods though the computation time for patch selection is relatively long. Part of our future research is to investigate how our method may improve DWI at even higher resolutions.Acknowledgements
This work was supported in part by the NIH grants NIBIB P41 EB027061 and NIH U01 EB025144.References
1. Bammer R. Basic principles of diffusion-weighted imaging. Eur J Radiol 2003;45(3):169-184.2. Buades A, Coll B, Morel JM. A non-local algorithm for image denoising. 2005 Ieee Computer Society Conference on Computer Vision and Pattern Recognition, Vol 2, Proceedings 2005:60-65.
3. Wiest-Daessle N, Prima S, Coupe P, Morrissey SP, Barillot C. Non-local means variants for denoising of diffusion-weighted and diffusion tensor MRI. Medical Image Computing and Computer-Assisted Intervention- Miccai 2007, Pt 2, Proceedings 2007;4792:344-+.
4. Andersson JLR, Sotiropoulos SN. Non-parametric representation and prediction of single- and multi-shell diffusion-weighted MRI data using Gaussian processes. Neuroimage 2015;122:166-176.
5. Manjon JV, Coupe P, Concha L, Buades A, Collins DL, Robles M. Diffusion Weighted Image Denoising Using Overcomplete Local PCA. Plos One 2013;8(9).
6. St-Jean S, Coupe P, Descoteaux M. Non Local Spatial and Angular Matching: Enabling higher spatial resolution diffusion MRI datasets through adaptive denoising. Med Image Anal 2016;32:115-130.
7. Veraart J, Novikov DS, Christiaens D, Ades-Aron B, Sijbers J, Fieremans E. Denoising of diffusion MRI using random matrix theory. Neuroimage 2016;142:384-396.
8. Moeller S, Pisharady PK, Ramanna S, et al. NOise reduction with DIstribution Corrected (NORDIC) PCA in dMRI with complex-valued parameter-free locally low-rank processing. Neuroimage 2021;
9. Zhao YJ, Xiao LF, Zhang Z et al. Jointly Denoise Diffusion-weighted Images Using a Weighted Nuclear Norm Minimization Approach. Proceedings of 29th International Society of Magnetic Resonance in Medicine 2021;P1334
10. Neher PF, Laun FB, Stieltjes B, Maier-Hein KH. Fiberfox: Facilitating the Creation of Realistic White Matter Software Phantoms. Magnet Reson Med 2014;72(5):1460-1470.
11. Sotiropoulos SN, Jbabdi S, Xu JQ, et al. Advances in diffusion MRI acquisition and processing in the Human Connectome Project. Neuroimage 2013;80:125-143.
12. Tian QY, Bilgic B, Fan QY, et al. DeepDTI: High-fidelity six-direction diffusion tensor deep learning. Neuroimage 2020;219.
13. Ma XD, Ugurbil K, Wu XP. Denoise magnitude diffusion magnetic resonance images via variance -stabilizing transformation and optimal singular -value manipulation. Neuroimage 2020;215.
14. Polimeni JR, Bhat H, Witzel T, Benner T, Feiweier T, Inati SJ, Renvall V, Heberlein K, Wald LL. Reducing sensitivity losses due to respiration and motion in accelerated echo planar imaging by reordering the autocalibration data acquisition. Magnetic Resonance in Medicine 2016;75(2):665-679.
15. Cauley SF, Polimeni JR, Bhat H, Wald LL, Setsompop K. Interslice leakage artifact reduction technique for simultaneous multislice acquisitions. Magnetic Resonance in Medicine 2014;72(1):93-102.
16. Sotiropoulos SN, Moeller S, Jbabdi S, Xu J, Andersson JL, Auerbach EJ, Yacoub E, Feinberg D, Setsompop K, Wald LL, Behrens TEJ, Ugurbil K, Lenglet C. Effects of image reconstruction on fiber orientation mapping from multichannel diffusion MRI: Reducing the noise floor using SENSE. Magnetic Resonance in Medicine 2013;70(6):1682-1689.
17. Jenkinson M, Beckmann CF, Behrens TE, Woolrich MW, Smith SM. Fsl. Neuroimage 2012;62(2):782-790.
Figures
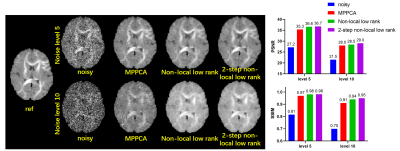
FIG. 1.
Comparison between different methods using
simulation data from fiberfox. Two noise levels 5, 10 are tested respectively
as shown in the first row and second row. PSNRs and SSIMs are also compared.
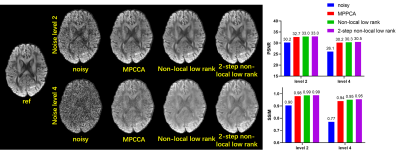
FIG. 2. Comparison between different
methods using simulation data from HCP. Single shell data of 36 directions is
used. Two noise levels 2, 4 are tested respectively as shown in the first row
and second row. PSNRs and SSIMs are also compared.
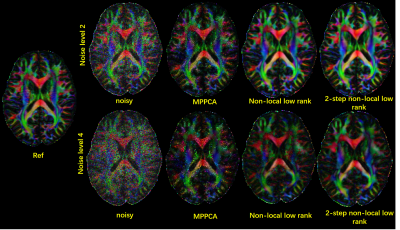
FIG.
3. cFA results of different denoising methods for simulation data from HCP. Reults
of two noise levels are shown.
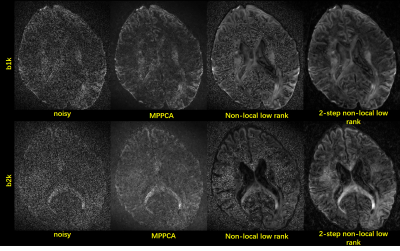
FIG.
4. Results of 0.7×0.7×0.7mm3 resolution
DWI images are shown. The two-shell data has 53 directions. Images of one b1k
and one b2k direction are shown.
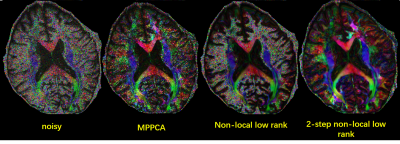
FIG.
5 cFA results of different denoising methods for 0.7×0.7×0.7mm3 resolution
DWI images.
DOI: https://doi.org/10.58530/2022/3041