2931
Simultaneous Multi Slice using Hadamard like encoding with non-Hadamard factors
Sudhir Ramanna1, Harsh Agarwal1, Rajagopalan Sundaresan1, Sajith Rajamani1, Ashokkumar P Reddy1, Bhairav Mehta1, and Ramesh Venkatesan1
1GE Healthcare, Bangalore, India
1GE Healthcare, Bangalore, India
Synopsis
Multiplexing of slices using the NEX/averaging dimension is an option for clinical MR protocols to improve SNR without imposing a scan time penalty. Hadamard encoding and decoding imposes Hadamard factors as limits where in only powers of 2 is used. We propose to use a Hadamard like encoding scheme but decode differently to yield a reduced effective NEX and improved motion sensitivity. This enables us to use any integer multiband factors.
INTRODUCTION
Simultaneous multi slices (SMS) or multiband 1-5 are used to increase slice coverage or reduce scan time. Some use coil sensitivities of multi-channel coils and some use Hadamard/Slider4,6 with multi-average scans. Hadamard is good for 2,4,8 multi-slice factors with matrix condition 1 and gSlider is best for maximum SNR in each acquisition but have increased motion sensitivity. Here, we show SMS with non-Hadamard integer factors that have good clinical relevance with reduced motion sensitivity.The SMS advantage of exciting adjacent slices simultaneously avoids multi-banding the SAR restraining refocusing pulse with higher flip angles. Instead, slice thickness of the existing refocusing pulse is increased. This technique shows an encoding/decoding scheme to SMS adjacent slices and achieve any integer SMS factors like 3,5,6 and 7. It is common to see MR clinical protocols with multiple NEX (averaging) to increase SNR (signal to noise). Here we use different RF excitations over various NEX to keep scan time similar and achieve multiple slice excitation/separation.
METHODS
Experiments were conducted on GE 1.5T Signa Creator. In the encoding scheme for each NEX, multiple slices are excited differently (ex. 3 slices). The concept can be extended to other SMS integer factors like 5,6,7. RF1 = Excitation pulse used in gradient/spin-echo sequence (Fig.1). Three differently modulated RF1 excitation pulses are used in the three NEX to generate signals S1, S2, S3. Modulation is achieved by multiplying RF1 pulse with cosine and sine (with frequency w0) and added to original RF1.Decoding individual slices (A, B, C) from measured signals S1, S2, S3 is done using matrix inversion of a linear system but with lower number of acquired signals. This results in a reduced effective NEX as only fewer signals are used in reconstruction. For SMS 3 factor, 2 signals were used. For SMS 5,6 and 7 factors, 4 signals were used to separate the 5, 6 and 7 multi-excited slices. The advantage is that different slices are separable using simple addition and subtraction operations and resultant slices are less motion sensitive. We show an example of the decoding mechanism to decode individual slices and other factors may be possible.
S1+S2=2C
S1-S3=2A
S3-S2=2B
RESULTS & DISCUSSION
Fig.2 shows simulation results of 3 different slice profiles (A, B, C) using Block Equations for a gradient echo sequence. It shows slice separation after excitation by 3 different RF1 modulated pulses in 3 NEX.In regular Hadamard decoding schemes, all signals are used for decoding/separation into 2 or 4 slices. Here, we use a specific set of signals (lower than acquired) to decode 3 slices separately as in Fig. 3. This uses a lower NEX than the three acquired but helps to achieve non-Hadamard integers and can be extended to other simultaneous slice excitations (5, 6, 7, …) using matrix inversion. Condition of the encoding matrix is 2 in the proposed technique. Fourier encoding is an alternative to explore with a reduced matrix condition. It makes the technique like a 3D sequence that encodes the different k-space partitions with different Fourier encodes. Encoding matrix conditions for g-Slider depends on the various encoding options used. Hadamard encoding with Hadamard matrix yields the best condition of the matrix as 1. Since a reduced set of signals is used for slice decoding, this technique is less motion sensitive as compared to the other Hadamard/Slider approaches that use all the excited signals.
This technique would reduce SAR of the SMS sequence drastically as the need for multibanding refocus pulse is voided and solves an important bottleneck in SMS adoption to commercial scanners. There is no need to verse the refocus pulse and existing simpler RF design methods/pulses can be used. Available Peak B1 of RF amplifier is used more efficiently for SMS of excitation pulse. This technique works best in low SNR scenarios where multi-NEX is a prerequisite to increase SNR. Simple additions and subtractions are used for slice separation.
CONCLUSION
In the Hadamard encoding/decoding scheme, the sequence is motion sensitive to all NEX since the signal from each excitation is used to decouple the slices. This technique shows fewer signals used to decouple slices that are Hadamard like encoded. It is less motion sensitive than the Hadamard technique. Multiplexing of multiple slices could be used to either reduce scan time in higher SNR scenarios or use similar scan time (as existing) to achieve more averages and improve SNR in lower SNR scenarios where multiple averages must be acquired for SNR reasons. Further, coil loop sizes are larger at low fields, and higher slice acceleration is possible without an associated g-factor/SAR penalty. This technique could be used to reduce SAR at higher fields for spin echo sequences. It could be used to improve slice coverage in anatomies where a new pass/acquisition is forced to achieve few more slices with the same TR/TE contrast. In low SNR regimes, when the bandwidth is reduced to improve SNR and number of slices allowed in the same acquisition gets reduced, SMS could enable multiple slices to get back the coverage. Sequences with fat sat reduce SNR in the imaged voxel and could be benefitted from SMS.Acknowledgements
Authors would like to thank Jeff Hopkins for discussion on RF pulses and Jeremy Heinlein for scanning.References
1. “Simultaneous multislice (SMS) imaging techniques”, Markus Barth, Felix Breuer, Peter J. Koopmans, David G. Norris, and Benedikt A. Poser, Magn Reson Med. 2016 Jan; 75(1): 63–81.2. “Simultaneous slice excitation and reconstruction for single shot EPI”, Nunes RG, Hajnal JV, Golay X, Larkman DJ, ISMRM 14th Annual Meeting, 2006, p. 293
3. “Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI”, Steen Moeller, Essa Yacoub, Cheryl A. Olman, Edward Auerbach, John Strupp, Noam Harel, Kâmil Uğurbil, Magn Reson Med 2010, Volume 63, Issue 5, Pages 1144-1153
4. “Fast submillimeter diffusion MRI using gSlider-SMS and SNR-enhancing joint reconstruction”,
Justin P. Haldar, Yunsong Liu, Congyu Liao, Qiuyun Fan, Kawin Setsompop, Magn Reson Med. 2020 Volume 84, Issue2, Pages 762-776
5. “Multiplexed echo planar imaging for sub-second whole brain fMRI and fast diffusion imaging”, Feinberg, D.A, S. Moeller, S.M. Smith, E. Auerbach, S. Ramanna, M.F. Glasser, K.L. Miller, K. Ugurbil, and E. Yacoub, PLoS ONE, 2010. 5(12): p. e15710.
6. “Multifrequency Selective rf Pulses for Multislice MR Imaging”, S. Muller, Magn Reson Med 6, 364-37 1 (1988)
Figures
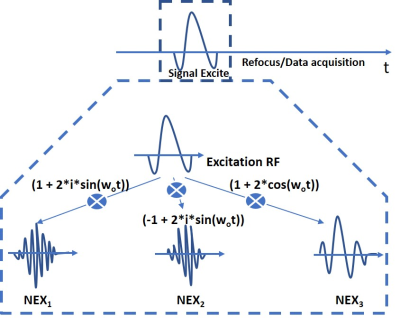
Fig.1
SMS Encoding scheme using 3 NEX. 3 different modulations of RF1 is
shown, RF2 could be an existing refocus pulse (for spin echo
sequences) that refocus all three SMS slices (not shown here). First, second
and third NEX is excited using three differently modulated RF1 excitation
pulses to generate signals S1, S2 and S3. S1=
RF1(1 + 2*cos(wot)), S2= RF1 (-1 +
2*i*sin(wot)) and S3= RF1 (1 + 2*i*sin(wot)).
The resultant combined pulse is a complex RF1 pulse.
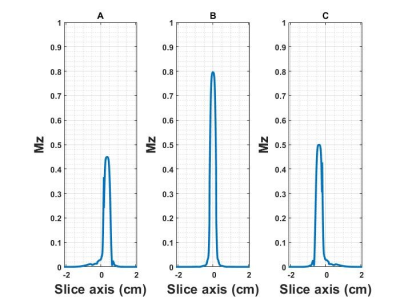
Fig.2) Simulation of
slice profile axis (after RF encoding and slice decoding) showing 3 distinct
slices (A, B and C) using Bloch Equations and ignoring relaxation effects, RF
pulse length << T2, T1. Starting magnetization of slice A, B and C in the
format [Mx, My, Mz] are [0 0 1], [0 0 0.65] and [0 0 0.8]. The modulated sinc
pulse has time bandwidth product = 4, RF pulse duration = 3.2ms, slice
thickness = 3.5mm, spacing = 0.3mm, flip = 90°.
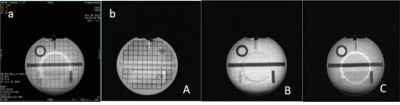
Fig.3a) Mixed SMS slice without decoding, 3b)
Separated slices A, B and C using standard ACR phantom. A 2d gradient echo
sequence was used to show the concept.
DOI: https://doi.org/10.58530/2022/2931