2928
Accelerated DeepRF using modified optimal control1Department of Electrical and Computer Engineering, Seoul National University, Seoul, Korea, Republic of
Synopsis
DeepRF1 is a recently proposed RF pulse design method using deep reinforcement learning and optimization, generating RF defined by a reward (e.g., slice profile and energy constraint) from self-learning. Here, we proposed an accelerated algorithm for DeepRF that utilizes a modified optimal control, replacing the computationally complex gradient ascent-based optimizer. The new algorithm is tested for slice-selective inversion and slice-selective excitation and compared with original DeepRF and SLR RF pulses, reporting improved computation efficiency while preserving performances. Additionally, a short-duration B1-insensitive inversion pulse, which was difficult to produce in conventional RF algorithms, is designed to demonstrate the usefulness of DeepRF.
Introduction
A recently proposed deep reinforcement learning (DRL)-powered RF pulse design method, DeepRF1, has successfully designed various types of RF pulses. The newly-designed pulses has reduced RF energy (ENG) compared to conventional design results, demonstrating the advantage of the method. It requires no training data nor knowledge of MR physics, adiabaticity, etc. because DRL performs self-learning via iterations. Furthermore, the method is flexible (i.e., generates various types of pulses) because the algorithm is driven only by a user-defined reward that includes slice profile specifications and RF energy. Despite these advantages, DeepRF is computationally demanding (~40 hours to design an RF pulse), limiting the applicability of the method. In this work, we redesign a part of DeepRF to reduce the computation time. The optimization step of DeepRF, which utilizes gradient ascent, takes roughly half of the computation and is replaced by a modified optimal control2-8. To test the performance of the new algorithm, slice-selective excitation and inversion pulses are designed. Additionally, a short-duration (2 ms) B1-insensitive volume inversion pulse, which is difficult to produce using a conventional approach, is designed, demonstrating the applications of DeepRF.Methods
[Modified Optimal Control]DeepRF consists of two steps: the DRL step designing a large number of seed RF pulses and the optimization step updating top-scored seed pulses for convergence. We replace the gradient-ascent algorithm in the optimization step with a modified optimal control method2. The modifications of the original optimal control are made as follows: Firstly, the design dimension is extended to the complex domain to have a flexibility in designing both magnitude and phase of an RF pulse (Table 1a). The original method was fixed to design a real part. Secondly, an analytic solution of the reward derivative is developed by hand because the optimal control needs matrix-wise formula and derivative of reward.
[RF generation and RF refinement]
For RF generation using DRL, a total of 3,840,000 seed pulses are generated. Then, the top 256 rewards RFs are optimized using the gradient ascent (original DeepRF or DRL+GA) or the modified optimal control (proposed DeepRF or DRL+mOC). To satisfy the slice profile and design specifications (stopband ripple condition, mean magnetization over bandwidth (BW), and peak amplitude limit), the following reward functions are used: i) slice-selective inversion pulse: L2 loss of the Mz between designed RF and Shinnar-Le-Roux9 (SLR), ii) slice-selective excitation pulse: mean Mxy in BW and max stopband ripple, iii) short-duration B1-insensitive volume inversion pulse: Mz in target inversion ranges and max amplitude term. An RF energy term is used in all pulses. The details are described in Table 1b. For the slice-selective inversion and excitation pulses, all design parameters are the same as those in the DeepRF paper1. For short-duration B1-insensitive volume inversion pulse, target inversion ranges of B1 and frequencies are from 0.5 to 2.0 and from -1000 Hz to 1000 Hz. DeepRF is implemented using PyTorch11 in RTX 8000.
[Conventional RF pulse designs]
The slice-selective inversion and excitation pulses are designed using SLR9. A short-duration (2 ms) B1-insensitive volume inversion pulse is created, following the hyperbolic secant10 (HS) design using a grid search.1
Results
For both slice-selective inversion and excitation pulses (Figs. 2 and 3), the RF shapes are different in all pulses but the slice profiles reveal comparable results (see tables). The RF energies of proposed DeepRF (DRL + mOC) and original DeepRF (DRL+GA) pulses demonstrate a reduction of 11.9% in inversion (both pulses) and 11.4% and 11.0% in excitation (proposed and original pulses, respectively) when compared to those of the SLR pulses. In Figure 4, the results of short duration B1-insensitive volume inversion pulse are shown. The mean Mz in the target inversion range of the proposed and original DeepRF pulses is -0.90 whereas that of HS is -0.76, demonstrating advantages of DeepRF. The computation times of the proposed DeepRF range from 3 to 3.4 hours in all pulses whereas they are from 10 to 17 hours for the original DeepRF, reporting substantial improvement.Conclusion and Discussion
In this study, we proposed an accelerated version of DeepRF which uses modified optimal control instead of gradient ascent. The results demonstrate that the modified optimal control can work with the same performance as the gradient ascent while reducing the computation time by 72 ± 11%. Additionally, DeepRF is demonstrated to design a short-duration B1-insensitive volume inversion pulse with satisfying mean Mz while the conventional method fails to meet the specification. The overall shapes of the RF pulses are different from those of gradient ascent but show similar performance such as RF energy and slice profile. The difference may stem from the learning rate and/or other parameters in the optimizers, reaching different local minima. Despite the advantages, optimal control has limitations: non-uniform frequency sampling seems to be difficult, and manual differentiation of the reward functions should be developed by hand. The computation time of DeepRF is still long due to the DRL step, which takes 23 hours1. The DRL step, however, was demonstrated to be effectively reduced to 4 hours at the cost of increased variability in reproduction.1 Hence, the total design time can be less than 8 hours and maybe further reduced with multi-GPU.Acknowledgements
This work was supported by Creative-Pioneering Researchers Program through Seoul National University(SNU), and Brain Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Science, ICT & Future Planning (NRF-2019M3C7A1031994).References
[1] Dongmyung Shin, et al. “Deep Reinforcement Learning Designed RadioFrequency Waveform in MRI.”, Nature Machine Intelligence, accepted (2021).
[2] Steven Conolly, et al. “Optimal Control Solutions to the Magnetic Resonance Selective Excitation Problem.” IEEE Transactions on Medical Imaging, 5.2 (1986): 106-115.
[3] Rund Armin, et al. “Magnetic resonance RF pulse design by optimal control with physical constraints.” IEEE Transactions on Medical Imaging, 37.2 (2017): 461-472.
[4] Vinding M.S, et al. “DeepControl: 2DRF pulses facilitating inhomogeneity and B0 off‐resonance compensation in vivo at 7 T.” Magnetic Resonance in Medicine, 85.6 (2021): 3308-3317.
[5] Vinding M.S, et al. “Fast numerical design of spatial-selective rf pulses in MRI using Krotov and quasi-Newton based optimal control methods.” The Journal of Chemical Physics, 137.5 (2012): 054203
[6] Vinding M.S, et al. “Local SAR, global SAR, and power‐constrained large‐flip‐angle pulses with optimal control and virtual observation points.” Magnetic Resonance in Medicine, 77 (2017): 374-384
[7] Skinner Thomas E, et al. "Reducing the duration of broadband excitation pulses using optimal control with limited RF amplitude." Journal of Magnetic Resonance, 167.1 (2004): 68-74
[8] Xu Dan, et al. "Designing multichannel, multidimensional, arbitrary flip angle RF pulses using an optimal control approach." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 59.3 (2008): 547-560
[9] John Pauly, et al. "Parameter relations for the Shinnar-Le Roux selective excitation pulse design algorithm (NMR imaging)" IEEE Transactions on Medical Imaging, 10.1 (1991): 53-65
[10] Silver M.S, et al. “Highly selective π2 and π pulse generation” Journal of Magnetic Resonance, 59 (1984): 347-351
[11] Paszke, A. et al. “PyTorch: An Imperative Style, High-Performance Deep Learning Library.” Advances in Neural Information Processing Systems, 32 (2019): 8024–8035.Figures
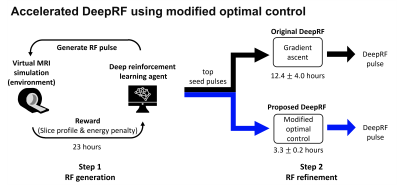
Fig. 1. Overview of accelerated DeepRF. In the first step of DeepRF, DRL generates seed for target RF properties defined by reward function. Then the top 256 reward seeds are selected as the input for optimization using either gradient ascent (original DeepRF) or modified optimal control (proposed DeepRF). The gradient ascent costs long computation time (12.4±4.0 hours) for convergence and is replaced by optimal control to reduce time (3.3±0.2 hours) while maintaining performance. Both methods show comparable performance in energy reduction and slice profile (see Figures 2-4).
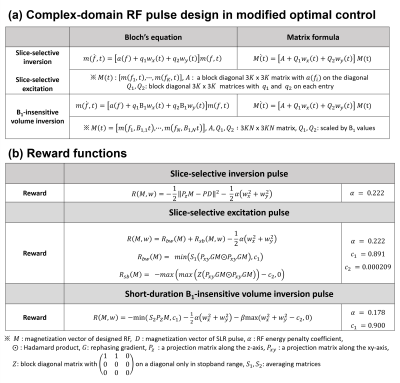
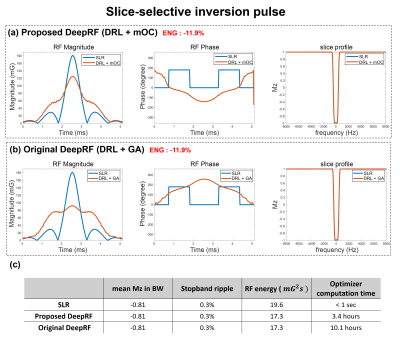
Figure 2. Comparison of the slice-selective inversion pulses using (a) proposed DeepRF (DRL with mOC) vs. SLR and (b) original DeepRF (DRL with GA) vs. SLR. The RF shapes of the proposed DeepRF and the original DeepRF are not the same but show comparable slice profiles (mean Mz in BW: -0.81, stopband ripple: 0.3%) to those of SLR and also have similar energy reduction (both 11.9% reduction). (c) Summary of the results. The computation time of modified optimal control (mOC) is reduced by 66% when compared to that of gradient ascent (GA).
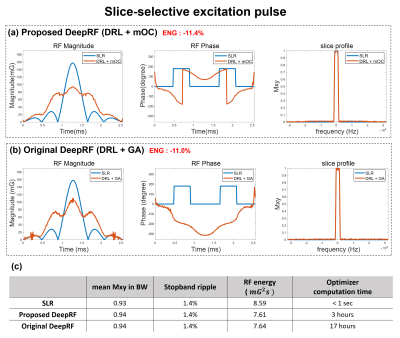
Figure 3. Comparison of the slice-selective excitation pulses (a) proposed DeepRF (DRL with mOC) vs. SLR and (b) original DeepRF (DRL with GA) vs. SLR. Both of the DeepRF methods show comparable slice profiles (both mean Mxy in BW: 0.94; stopband ripple: 1.4%) and energy reduction (Proposed: 11.4% reduction; Original: 11.0% reduction). (c) Summary of the results. The computation time of modified optimal control (mOC) is reduced by 80% when compared to that of gradient ascent (GA).
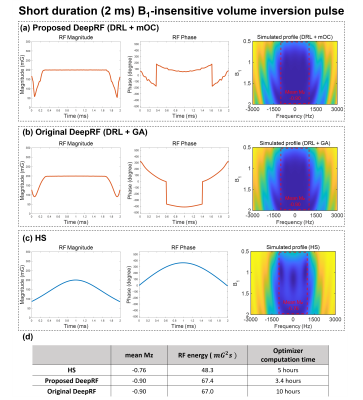
Figure 4. Comparison of the short-duration B1-insensitive volume inversion pulses using (a) proposed DeepRF (DRL with mOC), (b) original DeepRF (DRL with GA), and (c) hyperbolic secant (HS) design. The simulated mean Mz over target inversion range (B1: 0.5 - 2.0, off-resonance frequency: -1000 Hz - 1000Hz) is -0.90 in both DeepRF pulses whereas it is only -0.76 in the HS pulse, demonstrating a substantial improvement in the DeepRF pulses. (d) Summary of the results. The computation time of mOC is reduced by 66% when compared to that of GA.