2927
Optimal control pulse design as a low power alternative to BIR4 excitation pulses
Vencel Somai1,2, Alan J Wright1, Ming Li Chia1, and Kevin M Brindle1,3
1CRUK CI, University of Cambridge, Cambridge, United Kingdom, 2Department of Radiology, University Of Cambridge, Cambridge, United Kingdom, 3Department of Biochemistry, University of Cambridge, Cambridge, United Kingdom
1CRUK CI, University of Cambridge, Cambridge, United Kingdom, 2Department of Radiology, University Of Cambridge, Cambridge, United Kingdom, 3Department of Biochemistry, University of Cambridge, Cambridge, United Kingdom
Synopsis
The BIR4 pulse achieves adiabatic excitation over a moderate frequency range but has a relatively high adiabatic threshold, which is demanding on the hardware and deposits significant energy when the repetition rate is high. We show here using simulations and an experiment in vivo that optimal control can provide a better alternative with a significantly lowered adiabatic threshold.
Introduction
Optimal control radio frequency (RF) pulse design provides an efficient numerical framework for developing optimized RF pulses that show superior performance with respect to some user-defined target requirements, such as time-optimality, frequency selectivity and/or B1-insensitive behavior1-9. Producing highly uniform rotations that are immune to variation in the B1-field is of particular importance when surface coils are used for acquisition. Adiabatic pulses can achieve close to a uniform magnetization profile over a wide range of frequencies10, however the high adiabatic threshold and consequent energy deposition can be a problem with high repetition rates, for example in experiments with 2H. 2H magnetic resonance spectroscopic imaging has been shown recently to be a viable technique for metabolic imaging in the clinic and numerous studies have demonstrated its potential as a diagnostic tool11-17. Despite its low absolute sensitivity, the short relaxation time of deuterium allows for rapid signal averaging without saturation, thereby enabling metabolite detection. Rapid pulsing however makes the acquisition demanding both in terms of hardware requirements as well as specific absorption rate (SAR) constraints. Here we demonstrate that numerical optimal control-based pulse design could be used to design alternatives to the BIR4 pulse with similar performance but significantly lower adiabatic thresholds.Methods
The optimization used the built‐in fminunc() function with the default quasi-newton solver in MATLAB (The Mathworks, Natick, Massachusetts) run on the amplitude and phase of each pulse point of the shaped pulse.The cost function contains Bloch simulations and the simulated magnetization profile is compared to the desired magnetization profile in the squared function L2-norm on frequency-offset interval and B1 values ranging from 0 to 5 relative to the nominal pulse amplitude. Since RF coils and amplifiers cannot produce arbitrarily high B1 fields nor can they produce an instantaneous change in pulse amplitude the amplitudes of the shaped pulses were truncated to a maximum value of 1 G and then projected onto a set of waveforms with prescribed upper bounds on the first and second derivatives for each iteration of the optimization to yield a smooth amplitude variation18. Furthermore, unlike BIR4 pulses, the projected waveform starts and ends at 0 G, setting a more realistic task for the RF transmit chain. Five 2 ms long RF pulses were designed with flip-angles of 5, 15, 30, 68 and 90 degrees and starting the optimization from a linear-phase SLR pulse with 600 Hz wide pass-band. The results were compared to the corresponding 2 ms BIR4 pulses with respect to adiabatic threshold and overall performance over the and B1 grid. Relaxation was taken into account with a T1 value of 140 ms, and a T2 of 70 ms, typical of [2,3-2H2] fumarate13.The simulation results for a 2 ms 90 BIR4 pulse and an equivalent optimized pulse were validated with measurements of the natural abundance HDO peak in vivo in a BALB/c Nude mouse (Charles River Laboratories). Experiments were performed at 7T (Agilent, Palo Alto, California) using a home-built 10 mm diameter single-loop surface coil for 2H transmit and receive, which was positioned over the abdominal area of the mouse. The acquisition was the sum of 100 transients acquired into 1024 spectral points with a bandwidth of 4006 Hz. TR was set to 700 ms to allow full recovery of the magnetization. The transmit gain was arrayed in 20 steps to trace the adiabatic threshold of the pulses. The experiment was carried out in compliance with project and personal licenses issued by the UK Home Office, and approved by a local Animal Welfare and Ethical Review Body.Results
SimulationThe 2 ms long BIR4 pulses showed an approximately 1 G (~ 65%) higher adiabatic threshold when compared to the corresponding optimized pulses (Figure 1). A further advantage of the optimized design is the gradually decreasing flip-angle below the adiabatic threshold which is anticipated to mitigate edge effects when compared with the large variation observed with the BIR4 pulses.
In vivo experiment
The spectra of the HDO peak acquired in vivo showed good agreement with the simulated B1 profile of the 90 excitation pulses. The adiabatic threshold is reached at a power level approximately 60% lower with the optimized design than with the BIR4 pulse (Figure 2). The BIR4 pulse also had a 1.32 times higher normalized area, which taking into account the higher adiabatic threshold gave an SAR estimated to be 3.67 times higher than that of the optimized pulse.
Conclusion
Here we have shown that pulses designed by optimal control can offer a better solution to the B1-insensitive excitation problem than the adiabatic BIR4 pulses. A significant reduction in adiabatic threshold as well as SAR was observed and this superior performance was preserved in vivo.Acknowledgements
VS is in receipt of a Cambridge European Scholarship from the Cambridge Trust.References
1 Rosenfeld, D. & Zur, Y. Design of adiabatic selective pulses using optimal control theory. Magn Reson Med 36, 401-409, doi:10.1002/mrm.1910360311 (1996).2 Anand, C. K., Bain, A. D., Curtis, A. T. & Nie, Z. Designing optimal universal pulses using second-order, large-scale, non-linear optimization. Journal of Magnetic Resonance 219, 61-74, doi:https://doi.org/10.1016/j.jmr.2012.04.004 (2012).
3 Skinner, T. E., Reiss, T. O., Luy, B., Khaneja, N. & Glaser, S. J. Application of optimal control theory to the design of broadband excitation pulses for high-resolution NMR. Journal of Magnetic Resonance 163, 8-15, doi:https://doi.org/10.1016/S1090-7807(03)00153-8 (2003).
4 Skinner, T. E. et al. Optimal control design of constant amplitude phase-modulated pulses: Application to calibration-free broadband excitation. Journal of Magnetic Resonance 179, 241-249, doi:https://doi.org/10.1016/j.jmr.2005.12.010 (2006).
5 Conolly, S., Nishimura, D. & Macovski, A. Optimal control solutions to the magnetic resonance selective excitation problem. IEEE Trans Med Imaging 5, 106-115, doi:10.1109/tmi.1986.4307754 (1986).
6 Majewski, K. Simultaneous optimization of radio frequency and gradient waveforms with exact Hessians and slew rate constraints applied to kT-points excitation. Journal of Magnetic Resonance 326, 106941, doi:https://doi.org/10.1016/j.jmr.2021.106941 (2021).
7 Li, J.-S., Ruths, J., Yu, T.-Y., Arthanari, H. & Wagner, G. Optimal pulse design in quantum control: A unified computational method. Proceedings of the National Academy of Sciences 108, 1879, doi:10.1073/pnas.1009797108 (2011).
8 Rund, A., Aigner, C. S., Kunisch, K. & Stollberger, R. Simultaneous multislice refocusing via time optimal control. Magnetic Resonance in Medicine 80, 1416-1428, doi:https://doi.org/10.1002/mrm.27124 (2018).
9 Williams, S., Nielsen, J.-F., Fessler, J. & Noll, D. in International Society for Magnetic Resonance in Medicine (Montreal, 2019).
10 Garwood, M. & DelaBarre, L. The Return of the Frequency Sweep: Designing Adiabatic Pulses for Contemporary NMR. Journal of Magnetic Resonance 153, 155-177, doi:https://doi.org/10.1006/jmre.2001.2340 (2001).
11 De Feyter, H. M. et al. Deuterium metabolic imaging (DMI) for MRI-based 3D mapping of metabolism in vivo. Sci Adv 4, eaat7314, doi:10.1126/sciadv.aat7314 (2018).
12 Kreis, F. et al. Measuring Tumor Glycolytic Flux in Vivo by Using Fast Deuterium MRI. Radiology 294, 289-296, doi:10.1148/radiol.2019191242 (2019).
13 Hesse, F. et al. Monitoring tumor cell death in murine tumor models using deuterium magnetic resonance spectroscopy and spectroscopic imaging. Proceedings of the National Academy of Sciences 118, e2014631118, doi:10.1073/pnas.2014631118 (2021).
14 Polvoy, I. et al. Deuterium Metabolic Imaging-Rediscovery of a Spectroscopic Tool. Metabolites 11, 570, doi:10.3390/metabo11090570 (2021).
15 Batsios, G. et al. Pan-cancer imaging of TERT expression using deuterium magnetic resonance spectroscopy-based assessment of pyruvate metabolism. bioRxiv, 462047, doi:10.1101/2021.10.05.462047 (2021).
16 Ruhm, L. et al. Deuterium Metabolic Imaging in the human brain at 9.4 Tesla with high spatial and temporal resolution. NeuroImage 244, 118639, doi:10.1016/j.neuroimage.2021.118639 (2021).
17 Zhang, G. & Keshari, K. Deuterium Metabolic Imaging of Pancreatic Cancer. NMR in Biomedicine 34, e4603, doi:10.1002/nbm.4603 (2021).
18 Chauffert, N., Weiss, P., Kahn, J. & Ciuciu, P. A Projection Algorithm for Gradient Waveforms Design in Magnetic Resonance Imaging. IEEE Trans Med Imaging 35, 2026-2039, doi:10.1109/tmi.2016.2544251 (2016).
Figures
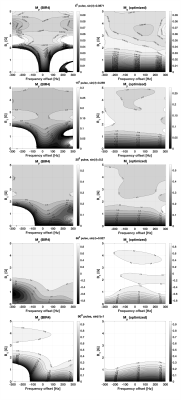
Bloch simulation of the magnetization immediately after a 2 ms BIR4 pulse (left column) and the optimized pulse (right column) with flip angles of 5, 15, 30, 68 and 90°. The ideal magnetization My,ideal = sin(FA) is shown in each case. The adiabatic threshold is ~1 G lower with the optimized pulses and the magnetization variation below this threshold is significantly less compared to that produced by the BIR4 pulses. Relaxation was taken into account.

(A) Amplitude and phase of the 2 ms BIR4 pulse. (B) Amplitude and phase of the corresponding optimized pulse. Both pulses had a flip-angle of 90 degrees and were used in the in vivo (C). In addition to the reduction in the adiabatic threshold, the optimized pulse maintained a lower shape factor too and started and ended at the physically realistic value of 0 G.
DOI: https://doi.org/10.58530/2022/2927