2925
Pulse design for joint optimization of semisolid saturation and free water rotation
David Leitão1,2, Raphael Tomi-Tricot1,3, Pip Bridgen1, Tom Wilkinson1, Patrick Liebig4, Rene Gumbrecht4, Dieter Ritter4, Sharon Giles1, Ana Baburamani1, Joseph V. Hajnal1,5, and Shaihan J. Malik1,5
1Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 2London Collaborative Ultra high field System (LoCUS), London, United Kingdom, 3MR Research Collaborations, Siemens Healthcare Limited, Frimley, United Kingdom, 4Siemens Healthcare GmbH, Erlangen, Germany, 5Centre for the Developing Brain, King's College London, London, United Kingdom
1Biomedical Engineering and Imaging Sciences, King's College London, London, United Kingdom, 2London Collaborative Ultra high field System (LoCUS), London, United Kingdom, 3MR Research Collaborations, Siemens Healthcare Limited, Frimley, United Kingdom, 4Siemens Healthcare GmbH, Erlangen, Germany, 5Centre for the Developing Brain, King's College London, London, United Kingdom
Synopsis
In MT imaging, particularly at ultra-high field, results can be influenced by spatial variations in both (1) on-resonance flip angle and (2) RF saturation specified by B1rms including on- and off-resonance contributions. Conventional pulse design with parallel transmission focuses on homogenizing flip angle (α) distributions but does not explicitly account for B1rms distribution.
In this work we propose a generalized pulse design framework that considers both α and B1rms and apply it to achieve uniform excitation and saturation at the same time. Performance is confirmed in phantom experiments at 7T, resulting in more uniform MTR compared to conventionally-designed pulses.
Introduction
Imaging at ultra-high field (≥7T) can be challenging due to the increased inhomogeneity in the radiofrequency and static magnetic fields, $$$B_1^+$$$ and $$$B_0$$$, and restrictive SAR constraints. Parallel transmit (pTx)1 provides flexibility in the pulse design to overcome these challenges, and can achieve more uniform flip angle distributions. Conventional pulse designs targeting flip angle2 ($$$\alpha$$$) are not applicable for design of pulses intended to saturate semisolid magnetization, since the semisolid $$$T_2$$$ is too short for the magnetization to be rotated by normal RF pulses. The recently proposed PUSH3,4 design framework instead designs pulses based on their root-mean-squared $$$B_1^+$$$ ($$$\beta$$$), which can then be used to directly control saturation of the semisolid. This has so far been applied to design of off-resonance saturation pulses that do not excite the water magnetization directly.However, magnetization transfer imaging also requires excitation pulses to create images. These can interact with the semisolid magnetization in two ways: (1) these pulses may themselves have non uniform $$$\beta$$$; and (2) non-uniform $$$\alpha$$$ (i.e., rotation of the water magnetization) will transfer to the semisolid pool. These effects are illustrated in Figure 1 which shows simplified simulations of a MT-weighted (MTw) gradient echo scan with saturation pre-pulse: part A shows the case for a non-uniform saturation pulse and part B shows the effect for an idealized perfectly uniform saturation pulse. Even assuming the latter case (as might be achieved by PUSH) both non-uniform $$$\alpha$$$ and non-uniform $$$\beta$$$ of the excitation pulse can lead to a non-uniform achieved MT ratio (MTR).
In this work we propose a pulse design method that considers both $$$\alpha$$$ and $$$\beta$$$ and apply it to design of excitation pulses for MT imaging at 7T.
Theory
Conventional pTx pulse design optimizes RF and gradient waveforms5, $$$\mathrm{b}$$$ and $$$\mathrm{k}$$$ respectively, to obtain a desired flip angle distribution $$$\alpha_{des}$$$. On the other hand, PUSH design optimises RF pulses to obtain a desired $$$\beta$$$ distribution $$$\beta_{des}$$$. In this work we propose a generalized pulse design that considers both flip angle $$$\alpha$$$ and $$$\beta$$$ properties:$$\begin{equation}\begin{aligned}\mathrm{\left\{\mathbf{\hat{b}},\mathbf{\hat{k}}\right\}=\underset{\mathbf{b,k}}{\arg\min}\left\{\frac{1-\lambda}{{\|\alpha_{des}\|_2}}\|\alpha(\mathbf{b,k})-\alpha_{des}\|_2+\frac{\lambda}{\|\beta_{des}\|_2}\|\beta(\mathbf{b})-\beta_{des}\|_2\right\}}\quad\quad[1]\\\mathrm{s.t.\,\quad{}SAR\,\,constraints\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\,\,\,\,}\\\mathrm{Hardware\,\,constraints\,\,\,\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad}\end{aligned}\end{equation}$$
where $$$\lambda{}\in[0,1]$$$ balances between error in $$$\alpha$$$ and $$$\beta$$$. If $$$\lambda{}=0$$$ then Eq.[1] reduces to the conventional pulse design that optimizes just for $$$\alpha$$$. If $$$\lambda{}=1$$$ Eq.[1] reduces to the PUSH design that optimizes just for $$$\beta$$$.
It is necessary to ensure the two targets $$$\alpha_{des}$$$ and $$$\beta_{des}$$$ are not incompatible. Considering a target $$$\alpha_{des}$$$ then the minimum $$$\beta$$$ required to achieve it is
$$\begin{equation}\mathrm{\beta_{min}=\frac{\alpha_{des}}{\gamma\sqrt{TR\,\tau\,p_1^2\,p_2}}}\quad\quad[2]\end{equation}$$
where $$$\mathrm{TR}$$$ is the repetition time, $$$\tau$$$ is the RF duration, and $$$\mathrm{p_1}$$$ and $$$\mathrm{p_2}$$$ are the integrals of the amplitude and squared amplitude of the normalized RF waveform ($$$\mathrm{p_1}=\mathrm{p_2}=1$$$ for a rectangular pulse).
Methods
The proposed pulse design (Eq.[1]) was tested in simulations using kT-points6 pulses with $$$\mathrm{\tau=1ms}$$$, $$$\mathrm{\alpha_{des}=16^\circ}$$$ and for a range of $$$\beta_{des}$$$ and $$$\lambda$$$.Experiments were conducted on a 7T scanner (MAGNETOM Terra, Siemens Healthcare, Erlangen, Germany) in prototype research configuration, with an 8-TX-channel head coil (Nova Medical, Wilmington MA, USA) using spoiled gradient-recalled-echo sequences (SPGR; Figure 2). A phantom (thermally denatured egg white) was scanned using MTw and non-MTw SPGR with $$$\alpha=\{4^\circ,16^\circ\}$$$ and $$$\mathrm{TR=20ms}$$$ to calculate MTR maps. The excitation pulse was designed using (i) circular polarized (CP) mode; (ii) 5 kT-points $$$\lambda{}=0$$$ (conventional pulse design); or (iii) 5 kT-points $$$\lambda=0.5$$$. The saturation pulse for the MTw scans was designed using (i) CP mode or (ii) PUSH applied at an offset frequency $$$\mathrm{\Delta=-2kHz}$$$ and $$$\beta_{des}=1.2\mu{}T$$$ optimized only over a mid-axial slice. $$$B_1^+$$$ and $$$B_0$$$ mapping were done using AFI7,8 and low flip angle SPGR sequences, prior to pulse optimization which was fully scanner-integrated within Matlab (MathWorks, Natick, MA, USA).
Results & Discussion
Figure 3 shows the errors in $$$\alpha$$$ and $$$\beta$$$ for different kT-points designs as a function of $$$\lambda$$$. For $$$\beta_{des}<\beta_{min}$$$ the error in $$$\alpha$$$ and $$$\beta$$$ increases rapidly when moving away from $$$\lambda=0$$$ and $$$\lambda=1$$$, respectively. For $$$\beta_{des}>\beta_{min}$$$ it is possible to obtain a good solution for both quantities ($$$\lambda=0.5$$$ – Figure 3D).Figure 4 shows acquired MTR maps. Use of PUSH (homogenized saturation pulse) led to improved MTR, but the effect of the excitation pulse was still apparent particularly for $$$\alpha=16^\circ$$$ (part B). KT-points improves the MTR homogeneity, however when $$$\lambda=0$$$ this is compromised by the excitation pulse producing non-uniform $$$\beta$$$ (also illustrated in Figure 3C). Design with $$$\lambda=0.5$$$ corrects this.
Conclusion
This work proposed a pTx pulse design that jointly homogenizes $$$\alpha$$$ and $$$\beta$$$; the latter is not directly influenced by applied gradients while the former is. This approach is necessary for proper correction of $$$B_1^+$$$ inhomogeneity effects in MTw sequences even if saturation pulses are designed independently with uniform properties. In addition to MTw imaging, these methods would also apply to quantitative methods such as MPM9,10 which uses essentially the same sequence structure. Phantom imaging at 7T showed improvement in MT contrast homogeneity from the proposed design compared to the conventional design that only homogenizes the flip angle.Acknowledgements
The authors wish to thank Alexis Amadon and Franck Mauconduit (NeuroSpin, CEA Paris-Saclay, Gif-sur-Yvette, France) for providing the AFI sequence and reconstruction. This work was supported by the King’s College London & Imperial College London EPSRC Centre for Doctoral Training in Medical Imaging [EP/L015226/1] and by core funding from the Wellcome/EPSRC Centre for Medical Engineering [WT203148/Z/16/Z] and by the National Institute for Health Research (NIHR) Biomedical Research Centre based at Guy’s and St Thomas’ NHS Foundation Trust and King’s College London and/or the NIHR Clinical Research Facility. The views expressed are those of the author(s) and not necessarily those of the NHS, the NIHR or the Department of Health and Social Care.References
1. Padormo, F., Beqiri, A., Hajnal, J. V & Malik, S. J. Parallel transmission for ultrahigh-field imaging. NMR in Biomedicine 29, 1145–1161 (2016).2. Grissom, W. et al. Spatial domain method for the design of RF pulses in multicoil parallel excitation. Magn. Reson. Med. 56, 620–629 (2006).
3. Leitão, D. et al. Uniform Magnetization Transfer contrast at 7T with Direct Saturation Control. in Proc. Intl. Soc. Mag. Reson. Med. 28, 0607 (2020).
4. Leitão, D. et al. Parallel transmit PUlse design for Saturation Homogeneity (PUSH) for Magnetization Transfer imaging at 7T. Submitt. to MRM (in Rev. (2021).
5. Pauly, J., Nishimura, D. & Macovski, A. A k-space analysis of small-tip-angle excitation. J. Magn. Reson. (1989). doi:10.1016/0022-2364(89)90265-5
6. Cloos, M. A. et al. KT-points: Short three-dimensional tailored RF pulses for flip-angle homogenization over an extended volume. Magn. Reson. Med. 67, 72–80 (2012).
7. Yarnykh, V. L. Actual flip-angle imaging in the pulsed steady state: A method for rapid three-dimensional mapping of the transmitted radiofrequency field. Magn. Reson. Med. 57, 192–200 (2007).
8. Nehrke, K. On the steady-state properties of actual flip angle imaging (AFI). Magn. Reson. Med. 61, 84–92 (2009).
9. Weiskopf, N. & Helms, G. Multi-parameter mapping of the human brain at 1mm resolution in less than 20 minutes. Proc. 16th Sci. Meet. Int. Soc. Magn. Reson. Med. 2241, (2008).
10. Wang, D., Stirnberg, R., Pracht, E. & Stöcker, T. Optimization of fast Quantitative Multiparameter Mapping (MPM) at 7T using parallel transmission. in Proc Intl Soc Mag Reson Med 29 3055 (2021).
Figures
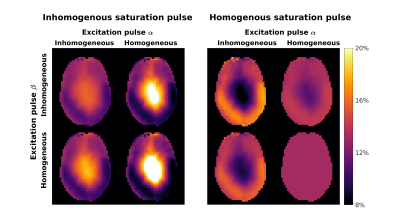
Figure 1 – MTR simulations assuming an inhomogeneous saturation pulse (left) and a homogeneous saturation pulse (right). For each case both properties $$$\alpha$$$ and $$$\beta$$$ of the excitation pulse are alternately assumed to be either homogeneous or inhomogeneous, so to observe the impact of each one on the MT contrast uniformization. In this case the pattern from CP mode was used for the inhomogeneous profiles.
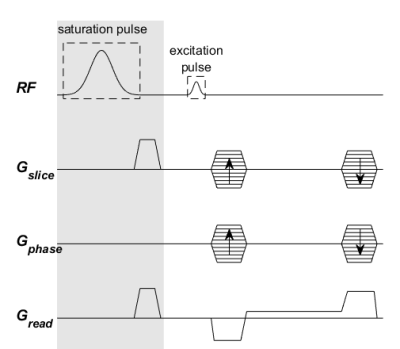
Figure 2 - Sequence diagram of the SPGR sequence used. The excitation pulse was designed with CP mode or kT-points with 5 sub-pulses (sub-pulse duration $$$100\mu{}s$$$, gradient blip duration $$$50\mu{}s$$$). The saturation pulse block in gray was only present in MT-weighted sequences and was designed with CP mode or PUSH-2 (sub-pulse duration $$$\mathrm{4ms}$$$).
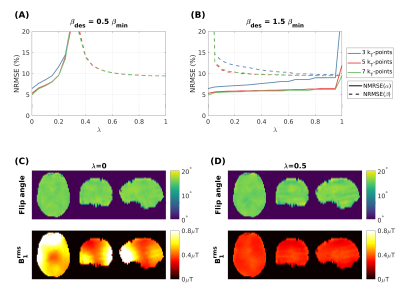
Figure 3 - Normalized mean squared error (NRMSE) of $$$\alpha$$$ (solid line) and $$$\beta$$$ (dashed line) of kT-points optimized using different number of sub-pulses, $$$\lambda$$$ and for (A) $$$\beta_{des}=0.5\beta_{min}=0.11\mu{}T$$$ and (B) $$$\beta_{des}=1.5\beta_{min}=0.33\mu{}T$$$. Flip angle and $$$B_1^{rms}$$$ maps for 5 kT-points ($$$\beta_{des}=1.5\beta_{min}$$$) with (C) $$$\lambda=0$$$ and (D) $$$\lambda=0.5$$$.
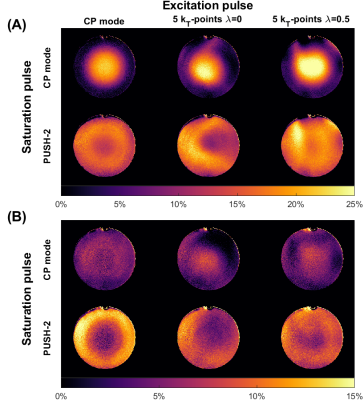
Figure 4 – MTR maps from phantom imaging with (A) $$$\alpha=4^\circ$$$ and (B) $$$\alpha=16^\circ$$$. Columns have different excitation pulses (left to right: CP mode, 5 kT-points $$$\lambda=0$$$, 5 kT-points $$$\lambda=0.5$$$) and rows have different saturation pulses (top to bottom: CP mode, PUSH-2).
DOI: https://doi.org/10.58530/2022/2925