2914
Deep prior for suppressing noise amplification and edge preservation in Phase-based EPT with Low-SNR image1Department of Electrical and Electronic Engineering, Yonsei University, Seoul, Korea, Republic of
Synopsis
Phase-based EPT algorithm is extremely sensitive to noise. Although many studies have investigated such as linear(Gaussian filter) or non-linear filter(TV norm) to cope with amplification, textured noise and staircasing effect still remain in phase image, which lead to conductivity error such as broadening boundary artifact or high std value in reconstructed conductivity maps. In this study, we propose a deep prior based denoising method, which achieve to not only suppress instability brought by noise amplification but reduce boundary error.
Introduction
Phase-based EPT1 is a non-invasive technique to reconstruct tissue electrical property using only transceiver phase information from spin-echo or bSSFP sequence. However, this algorithm is extremely sensitive to noise due to the Laplacian operator. Many studies have investigated such as linear8 or non-linear filters2,3 to cope with noise amplification with edge preservation, but textured noise4(broadening boundary artifact) and staircasing effect5 are still remained in these methods which lead to conductivity error. To dealing with this problem, we proposed deep prior method that the convolutional neural network architecture itself can act as a prior without any training dataset6, thereby replacing the regularization term to solve image denoising task.In this study, we investigated the performance of the deep priors to suppress noise amplification and edge preservation for conductivity reconstructions with low-SNR data. We applied the deep prior to real and imaginary components of MR data, and the denoised data was recombined to B1 phase for conductivity reconstructions. Then the proposed algorithm was compared with conventional filtering methods (e.g., Gaussian filter, Total variation filter). To investigate the denoising performance, we applied the Laplacian-based and integral-based7 conductivity reconstruction algorithms to B1 phase with each denoising method.
Theory
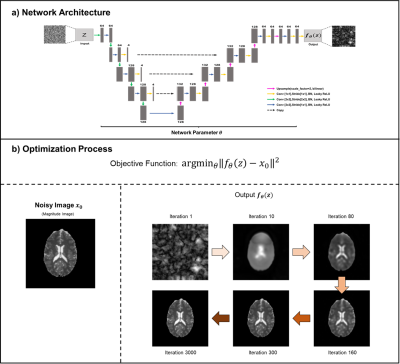
[Denoising Technique]The forward model of conductivity reconstruction with denoising filter can be written as model-based data consistency term with regularization2,3:
$$\hat{\sigma}=arg\min[\parallel Cond(\phi^{+})-\sigma\parallel^{2}+\lambda R(\phi^{+})] [1]$$
$$$Cond(\cdot)$$$ is conductivity reconstruction function. In this study, we drop the explicit TV regularization2,3 R(x) and replacing it with implicit prior, which captured by the neural network parametrization. The expression can be rewritten as follow:
$$\theta^{*}=arg\min \parallel f_{\theta}(z)-x_{0} \parallel^{2} [2]$$
The $$$f_{\theta}(\cdot)$$$ is CNN as shown in Fig 1. The $$$x_{0}\in R^{H\times W\times 2}$$$ is the combined real and imaginary parts with 2 channels from dataset, and the tensor $$$z\in R^{H\times W \times 32}$$$ is random Gaussian noise with 0.1 std. The minimizer $$$\theta^{*}$$$ is calculated using an ADAM optimizer, starting from a random initialization of the parameters $$$\theta$$$. Given the minimized $$$\theta^{*}$$$ , the denoised phase $$$\hat{\phi}^{+}$$$ is recombined from the denoised real and imaginary components $$$x^{*}=f_{\theta^{*}}(z)$$$, then conductivity is obtained from $$$\hat{\sigma}=Cond(\hat{\phi}^{+})$$$ .
[Reconstruction Technique]
Two different phase-based EPT reconstruction algorithms7 are implemented to investigate the denoising performance.
Laplacian based algorithm is differential equation, valid in slow varying regions: $$$\sigma =\triangledown^{2}\phi^{+}/\mu_{0}\omega [3]$$$ , $$$\mu_{0}$$$ = vacuum permeability, $$$\omega$$$ = Larmor frequency, and $$$\triangledown^{2}$$$ = Laplacian operator.
Integral based algorithm8 is integral form of equation 3: $$$\sigma = \oint \triangledown \phi^{+}ds/V\mu_{0} \omega [4]$$$, where S is the closed surface of some kernel with volume V.
Method
[Simulation Data]The simulation data was calculated from finite-difference time-domain (FDTD) simulation program9,10 (Sim4Life, Zurich Med Tech, Zurich, Switzerland). and fields were calculated in quadrature (QA) and anti-quadrature (AQ) modes with simulation Duke phantom inside a birdcage coil. The noisy simulation data (SNR10) was acquired by adding the random Gaussian noise to real and imaginary components of the complex-valued noiseless simulation data.
[In-vivo Data]
Turbo spin-echo (TSE) data were acquired at 3T: 1 healthy volunteer (Tim Trio, Siemens Healthineers: TR/TE=4500/85ms, resolution=1×1mm2, slice thickness=3mm)
Result
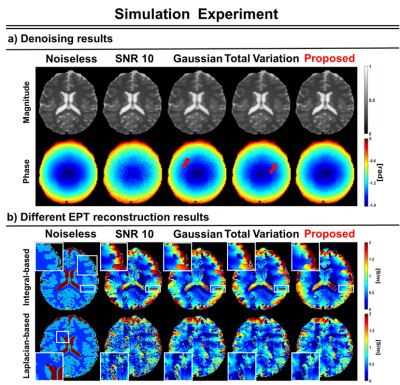
Figure 2 shows deep prior and other denoising methods performance on noisy simulation data. Two phase-based reconstruction techniques (Laplacian-based: 11x11 Laplacian kernel, Integral-based: 10x10 integral kernel) were applied to calculate conductivity map. Compared to GTC as a reference, the deep prior method (white box in integral method) shows less error in conductivity reconstruction map. Especially, the boundary error (white box in Laplacian method) is compensated compared to other denoising methods. On the other hand, there are textured noise and staircasing effect remained in Gaussian filter and TV norm phase map(red arrow) respectively.Figure 3 show the quantitatively analysis result of WM, GM CSF value for simulation data. Particularly in CSF region, the TV norm result shows higher std value than Gaussian or deep prior method. Deep prior method achieved highest SSIM as well as lowest RMSE among the denoising methods.
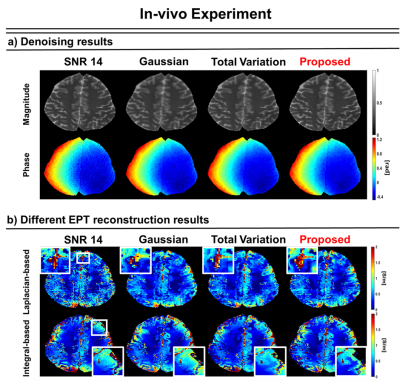
Figure 4 shows the results for the deep prior method and conventional denoising methods on in-vivo data. 12x12 Laplacian kernel and 12x12 Integral kernel were applied to reconstruct the denoised phase images. Deep prior method(white box) shows less error in CSF region and reduces the boundary artifact compared with other methods.
Discussion&Conclusion
In simulation and In-vivo data experiments, textured noise4 and staircasing effect5 were remained in phase map after applying the Gaussian filter and TV norm. These effects are directly propagated into conductivity reconstruction and cause conductivity error. Although the Gaussian filter shows a lower std value in different brain region, the drawback of Gaussian filter is broadening boundary artifact. As for TV norm, staircasing effect leads to high std value in different brain regions, but TV norm can achieve the reducing boundary error due to its edge-preserving function3. On the other hand, the proposed deep prior method not only suppresses the instability brought by noise amplification but reduces boundary artifact. Based on this observation, when the use of the denoising filters is inevitable, it may be an alternative for conductivity reconstructions. As a further study, more factors (i.e. more various scan parameters, image resolution, SNR levels, and applications for clinical data) will be investigated with network optimization.Acknowledgements
This work was supported by the National Research Foundation of Korea(NRF) grant funded by the Korea government(MSIT) (NRF-2019R1A2C1090635).References
1. T. Voigt. et al., Quantitative conductivity and permittivity imaging of the human brain using electrical properties tomography. Mag. Reson. Med., Vol 66(2), 2011, 456-466.
2. K. M. Ropella and D. C. Noll, “A regularized, model-based approach to phase-based conductivity mapping using MRI,” Magn. Reson. Med., vol. 78, no. 5, pp. 2011–2021, Nov. 2017
3. Borsic, A., Perreard, I., Mahara, A., and Halter, R. J. (2015). An inverse problems approach to MR-EPT image reconstruction. IEEE Trans. Med. Imaging 35, 244–256. doi: 10.1109/tmi.2015.2466082
4. Shin J., Kim J.H., Kim D.H. Redesign of the Laplacian Kernel for Improvements in Conductivity Imaging Using MRI. Magn. Reson. Med. 2019;81:2167–2175. doi: 10.1002/mrm.27528.
5. Lysaker M. Lundervold A. and Tai X.-C, “Noise removal using fourth-order partial differential equations with applications to medical magnetical resonance images in space and time”, IEEE Trans on Image Processing..12,12 2003, pp. 1579-1590
6. Ulyanov, D., Vedaldi, A., & Lempitsky, V. (2018). Deep image prior. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 9446-9454).
7. S. Bulumulla, S. K. Lee, and D. T. B. Yeo, “Calculation of electrical properties from maps—A comparison of methods,” in Proc. 20th Annu. Meet. ISMRM, Melbourne, Australia, 2012, p. 3469.
8. Anita Karsa. et al., New approaches for simultaneous noise suppression and edge preservation to achieve accurate quantitative conductivity mapping in noisy images. In Proc. 30th Annu.Meet. ISMRM
9. Christ A, et al. The Virtual Family—development of surface-based anatomical models of two adults and two children for dosimetric simulations. Physics in Medicine & Biology, 2009;55:N23.
10.Gosselin M-C, et al. Development of a new generation of high-resolution anatomical models for medical device evaluation: the Virtual Population 3.0. Physics in Medicine & Biology, 2014;59(18):5287.
Figures