2911
A Novel Volume-Surface Integral Equation Formulation of Global Maxwell Tomography: Simulations and Experiments.1Center for Advanced Imaging Innovation and Research (CAI2R), Department of Radiology, New York University Grossman School of Medicine, New York, NY, United States, 2The Bernard and Irene Schwartz Center for Biomedical Imaging (CBI), Department of Radiology, New York University Grossman School of Medicine, New York, NY, United States, 3Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, United States, 4Vilcek Institute of Graduate Biomedical Sciences, New York University Grossman School of Medicine, New York, NY, United States
Synopsis
Global Maxwell Tomography (GMT) is an inverse scattering technique that estimates electrical properties (EP) from magnetic resonance measurements. The original GMT relies on an approximation of the incident fields, which is not accurate for experiments, especially in-vivo. We propose a new GMT formulation, based on the volume-surface integral equation (VSIE) method, where we implicitly re-estimate the incident fields accounting for the updated EP in every GMT iteration. We show average EP reconstruction error below 8% for a uniform phantom experiment and below 10% for a simulation experiment with a heterogeneous head model and realistic SNR.
Introduction
At the high operating frequencies associated with ultra-high-field MRI, tissue electrical properties (EP) are encoded in the spatial distribution of the transmit field (B1+). Global Maxwell Tomography (GMT) reconstructs electric conductivity (σ) and relative permittivity (εr) from B1+ measurements by inverting the integral equation (IE) form of Maxwell’s equations. Accurate EP reconstructions were demonstrated for simulations using realistic head models and in experiments with homogeneous phantoms [1]. However, since GMT is based on volume IE (VIE), it requires an accurate approximation of the incident electromagnetic waves illuminating the sample [2]. While this is readily available in simulations where the sample EP are known, in actual experiments one is forced to use free-space incident fields ignoring their dependency on the unknown EP, which is less accurate, especially in-vivo. Here, we describe a volume-surface IE (VSIE) approach, which does not require knowledge of the true incident fields, but generates them using a simulated RF coil and updates them at each GMT iteration by solving the surface IE in the presence of the updated EP.Theory and Methods
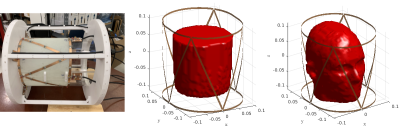
GMT reconstructs EP by iteratively minimizing the difference, over the volume of the sample, between measured B1+ and the B1+ simulated with the current EP estimates. In the original GMT implementation, the incident fields were assumed constant and only the scattered electromagnetic fields were re-calculated at each iteration to account for the updated EP by solving the VIE [3]. In our proposed method, we instead solve the VSIE to re-compute both the incident and scattered fields, since the former are affected by coil current perturbations due to back-scattering from the EM field inside the sample [4]. In particular, we used the VSIE described in [5], which relies on the precorrected FFT method [6]. We demonstrated our novel formulation, for two GMT reconstructions (5 mm isotropic resolution), with an 8 channel transceive array [3] (Figure 1) at 7 Tesla. The first case was an experiment using a cylindrical phantom filled with saline (Figure 1), with ground truth EP of εr = 79.4 and σ = 0.79 S/m, as measured with a dielectric probe (Agilent Technologies, Santa Clara, CA), for which the 8 individual B1+ maps were measured using magnetic resonance fingerprinting [7]. The second case was a simulation experiment, with a realistic head model [8] (Figure 1), where we computed synthetic B1+ measurements by solving a VSIE simulation with the ground-truth EP. The synthetic B1+ maps were corrupted with two different levels of Gaussian noise resulting in peak SNR equal to 200 and 150, respectively, which is a reasonable assumption at 7 Tesla MRI. Both GMT reconstructions were executed for 500 iterations starting from the same homogeneous initial guess (εr = 21.1 and σ = 0.13 S/m), which was far from the expected EP.Results
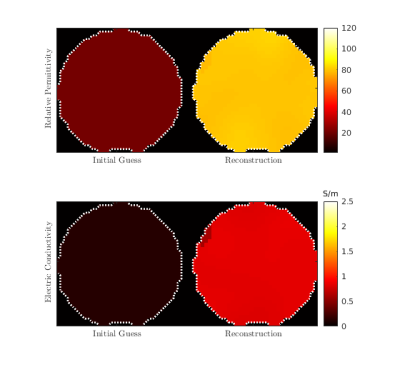
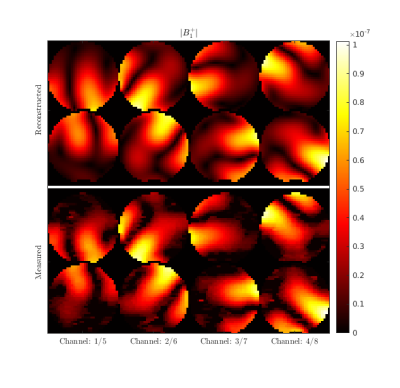
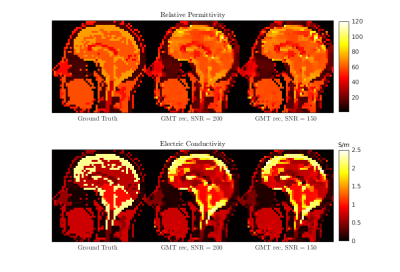
Figure 2 shows the initial guess and reconstructed EP for the central axial slice through the cylindrical phantom. The mean values were 80.1 (+- 3.3) and 0.83 S/m (+- 0.07 S/m) for εr and σ, respectively. In Figure 3 we show a qualitative comparison between the measured B1+ maps and the B1+ computed using the EP reconstructed by GMT for a representative axial slice. Figure 4. compares the ground-truth EP of the head model with the reconstructed EP. For peak SNR = 200 (mean SNR ranged from 28 to 42 for the 8 channels), the average peak normalized absolute error (PNAE) over the entire volume of the head was 8.38% and 5.39% for the relative permittivity and conductivity, respectively. For peak SNR = 150 (mean values: 26-39), the PNAE increased to 9.39% and 5.94% for εr and σ, respectively. Figure 5, shows the distribution of the PNAE for all voxels of the head model.Discussion and Conclusions
We demonstrated a novel VSIE-based GMT suitable for in-vivo experiments. Our VSIE formulation does not require prior knowledge of the incident electromagnetic fields, which was a limitation of the original VIE-based GMT formulation. The new GMT reconstructed EP for a realistic head model with the same accuracy as the original GMT, despite the fact that, unlike the original GMT, the new GMT could not rely on knowledge of the true incident fields [2]. The reconstruction error of the new VSIE-based GMT was also small for the phantom experiment. The difference between reconstructed EP and those measured with the probe was ~2% for the relative permittivity and ~7% for the conductivity. Note that these differences are comparable with the accuracy and repeatability of the dielectric probe measurements. Other possible sources of error could include experimental errors in B1+ measurement, temperature changes during the scan, etc. Future work will include multi-compartment phantom experiments and in-vivo validation. Furthermore, we are planning to explore other approaches that do not require explicit knowledge of the incident fields. For example, one could use an electromagnetic basis [9] as a constrained regularization technique to approximate the incident fields. In such a scenario, the VSIE-based GMT would transform to an equivalent VIE-based version, where both the EP and the basis coefficients would be estimated during the iterative optimization.Acknowledgements
This work was supported by NIH R01 EB024536 and by NSF 1453675. It was performed under the rubric of the Center for Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net), an NIBIB Biomedical Technology Resource Center (NIH P41 EB017183).References
[1] Serrallés, José EC, et al. "Noninvasive estimation of electrical properties from magnetic resonance measurements via global Maxwell tomography and match regularization." IEEE Transactions on Biomedical Engineering 67.1 (2019): 3-15.
[2] Giannakopoulos, Ilias I., et al. "Magnetic-resonance-based electrical property mapping using Global Maxwell Tomography with an 8-channel head coil at 7 Tesla: a simulation study."IEEE Transactions on Biomedical Engineering 68.1 (2020): 236-246.
[3] Georgakis, Ioannis P., et al. "A Fast Volume Integral Equation Solver with Linear Basis Functions for the Accurate Computation of EM Fields in MRI." IEEE Transactions on Antennas and Propagation (2020).
[4] Villena, Jorge Fernández, et al. "Fast electromagnetic analysis of MRI transmit RF coils based on accelerated integral equation methods." IEEE Transactions on Biomedical Engineering 63.11 (2016): 2250-2261.
[5] Guryev, G. D., et al. "Fast field analysis for complex coils and metal implants in MARIE 2.0." ISMRM (2019).
[6] Phillips, Joel R., and Jacob K. White. "A precorrected-FFT method for electrostatic analysis of complicated 3-D structures." IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 16.10 (1997): 1059-1072.
[7] Cloos, Martijn A., et al. "Multiparametric imaging with heterogeneous radiofrequency fields." Nature communications 7.1 (2016): 1-10.
[8] Christ, Andreas, et al. "The Virtual Family—development of surface-based anatomical models of two adults and two children for dosimetric simulations." Physics in Medicine & Biology 55.2 (2009): N23.
[9] Guérin, Bastien, et al. "The ultimate signal‐to‐noise ratio in realistic body models." Magnetic resonance in medicine 78.5 (2017): 1969-1980.
Figures