2905

Improved MP-PCA denoising through tensor generalization

Jonas Lynge Olesen^1,2, Andrada Ianus³, Noam Shemesh³, and Sune Nørhøj Jespersen^1,2
¹Center of Functionally Integrative Neuroscience (CFIN) and MINDLab, Aarhus University, Aarhus, Denmark, ²Department of Physics and Astronomy, Aarhus University, Aarhus, Denmark, ³Champalimaud Research, Champalimaud Centre for the Unknown, Lisbon, Portugal

Synopsis

A popular SNR-boosting method in MRI is denoising based on principal component analysis with automated rank estimation by exploiting the Marchenko-Pastur distribution of noise singular values (MP-PCA). MP-PCA operates by reshaping data-patches into matrices to discriminate signal from noise using random matrix theory. Here, we generalize MP-PCA to exploit tensor-structured data arising in, e.g., multi-contrast or multicoil acquisitions, without introducing new assumptions. As proof of concept, we demonstrate a substantial increase in denoising performance in a multi-TE DKI dataset, in particular for small sliding windows. This is beneficial especially in cases of rapidly varying contrast or spatially varying noise.

Introduction

MP-PCA^1,2 denoising is based on principal component analysis (PCA) and exploits the Marchenko-Pastur (MP) distribution of noise singular values for rank estimation. MP-PCA has become very popular for SNR-boosting with negligible signal loss or spatial smoothing^3-6 because of its effectiveness and objective rank estimation.

Information redundancy in MRI acquisitions (e.g. in directions in DTI or TE in T2 mapping) make typical MRI data well described by a low-rank approximation suitable for MP-PCA denoising. However, in many cases, multiple dimensions with redundancy exist, which opens opportunities for improved denoising. Here, we generalize matrix MP-PCA to tensor-structured data (tensor MP-PCA) and exploit the redundancy in multiple dimensions by applying MP rank-reduction to the higher-order singular value decomposition (HOSVD) recursively, without introducing new assumptions. Tensor MP-PCA performs as well or better than matrix MP-PCA in general, and we demonstrate substantial improvements in tensor-structure scenarios. Through objective rank estimation, recursivity, and shrinkage^4,8, tensor MP-PCA also outperforms classical HOSVD approaches⁷.

Theory

Matrix MP-PCA
MP-PCA^1,2 denoising applies a “sliding window” over voxels and denoises the resulting patches independently. Each patch forms a matrix $$$X$$$ with voxels as rows and one or more modalities (i.e. diffusion, relaxation, fMRI) as columns. SVD yields $$X=USV^\dagger$$ then noise components are removed based on the MP distribution of noise singular values (assuming iid noise with zero mean). Thereby estimating $$$\sigma^2$$$ and the signal subspace onto which $$$X$$$ is projected to yield a denoised $$$\tilde{X}$$$ $$\tilde{X}=\tilde{U}\tilde{U}^{\dagger}X=\tilde{U}\tilde{S}\tilde{V}^\dagger$$ where tilde signifies that noise components have been removed. Some improvement is attained by applying optimal shrinkage^4,8.

Tensor MP-PCA
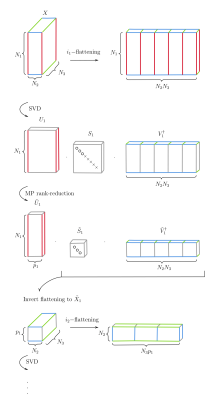
Given multiple dimensions, each patch can form a tensor. Assume for concreteness but without loss of generality that each patch is a three-index tensor $$$X_{i_1i_2i_3}$$$ (see Fig. 1) – for instance in dMRI with $$$i_1$$$ for voxels, $$$i_2$$$ for directions, and $$$i_3$$$ for b-values. Take $$$X$$$’s $$$i_1$$$-flattening $$$X_{i_1(i_2i_3)}$$$ (the parenthesis signifies index concatenation) and apply SVD and MP rank-reduction yielding $$$\tilde{U}\tilde{S}\tilde{V}^\dagger$$$. Define tensor $$$\tilde{X}_1\equiv\tilde{U}_1^{\dagger}X=[\tilde{S}_1\tilde{V}_1^\dagger]$$$, where it is implicit that $$$\tilde{U}^\dagger$$$ acts on index $$$i_1$$$ and $$$[\cdots]$$$ signifies inverting the previous flattening. $$$\tilde{X}_1$$$ retains $$$X$$$'s noise properties, since $$$\tilde{U}_1$$$ is unitary. Applying SVD and rank-reduction to the $$$i_2$$$-flattening of $$$\tilde{X}_1$$$ yields $$$\tilde{U}_2$$$ and $$$\tilde{X}_2\equiv\tilde{U}_2^{\dagger}\tilde{X}_1=[\tilde{S}_2\tilde{V}_2^\dagger]$$$ and so on. The recursive procedure stops at the last index after which $$\tilde{X}=\tilde{U}_1\tilde{U}_2\tilde{U}_3[\tilde{S}_3\tilde{V}_3^\dagger]$$ This reduces to matrix MP-PCA for matrices resulting in equal or better performance. It outperforms classical HOSVD approaches⁷, for which the rank has been determined a priori, through objective rank estimation and the recursive approach, which removes noise components at step $$$n$$$ before proceeding to $$$n+1$$$ - improving the $$$U_{n+1}$$$, $$$X_{n+1}$$$ estimates - rather than estimating all $$$U$$$ before rank-reduction. Furthermore, shrinkage is applicable to the last $$$\tilde{S}_n$$$.

Methods

All experiments were preapproved by the competent institutional and national authorities and were carried out in accordance with European Directive 2010/63.

For proof of concept, we employ a mouse brain dMRI dataset recorded at 16.4T using a microimaging probe with a multi-spin-echo sequence (FOV 10x8mm², matrix 100x80, 27 slices, in-plane resolution 0.1x0.1mm², slice-thickness 0.5mm, pulse width 3.5ms, pulse separation 5.6ms, 6 b-shells from 0.5 to 3ms/μm², 20 directions, and repeated for 10 TE from 10.7 to 35ms). Matrix and tensor MP-PCA are compared using the data and a numerical phantom created by generating a DKI signal (parameters from a DKI fit to actual data) for each TE and adding Gaussian noise with an SNR ($$$S_0/\sigma$$$) of twenty, ten b-shells, thirty-two directions, and one/ten TEs. Performance is quantified using the root-mean-squared-error (RMSE) between the denoised and ground truth images

Results and discussion

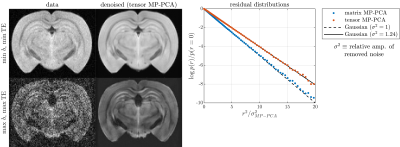
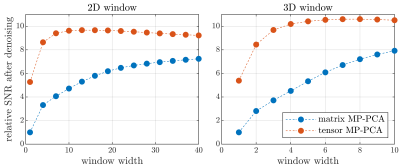
Fig. 1 shows data before and after applying tensor MP-PCA for the highest and lowest SNR scenarios. Residual distributions for tensor and matrix techniques are shown to be approximately Gaussian indicating that negligible signal variance is removed. For this dataset, tensor MP-PCA removes 24% more noise than matrix MP-PCA. Performance depends on several properties such as SNR, with better relative performance in low-SNR scenarios as suggested by the numerical phantom (Fig. 2).

Fig. 2 compares performance on multi-TE phantom data for various sliding window sizes. Tensor MP-PCA outperforms matrix MP-PCA for any window size, consistent with containing matrix PCA as a special case. Tensor MP-PCA reaches optimal performance at smaller patches, making it better suited for spatially varying noise or rapidly varying contrast. Additionally, the smaller patches reduces computation time.

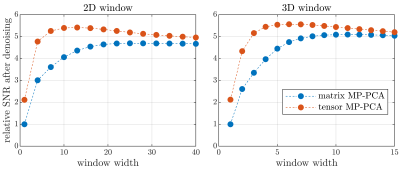
Fig. 3 compares performance on single-TE phantom data. Comparing Fig. 2 and 3 it is apparent that the tensor-structure from multiple TEs benefits tensor MP-PCA substantially. This opens several perspectives on particularly favorable applications such as multicoil³ or multimodality acquisitions^9-12. We also note that MRI data is inherently tensor-structured in terms of voxels with x, y, z indices. For the data considered here, however, we found that combining voxels in one index performs near optimal. Nevertheless, it is plausible that retaining the voxel tensor-structure could increase performance in other scenarios⁷.

Conclusion

We generalized MP-PCA to multidimensional data achieving improved performance in such scenarios. Tensor MP-PCA works well for smaller patches increasing speed and suitability to rapidly varying contrast and spatially varying noise. Since matrix MP-PCA is a special case of tensor MP-PCA and no new assumptions are introduced, tensor MP-PCA can be directly adopted wherever MP-PCA is applied.

Acknowledgements

The authors thank Martin Mikkelsen for support with the design and creation of illustrations.

SJ and JO are supported by the Danish National Research Foundation (CFIN), and the Danish Ministry of Science, Innovation, and Education (MINDLab). Additionally, JO are supported by the VELUX Foundation (ARCADIA, grant no. 00015963). NS was supported in part by the European Research Council (ERC) (agreement No. 679058). AI is supported by ”la Caixa” Foundation (ID 100010434) and European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 847648, fellowship code CF/BQ/PI20/11760029. The authors acknowledge the vivarium of the Champalimaud Centre for the Unknown, a facility of CONGENTO which is a research infrastructure co-financed by Lisboa Regional Operational Programme (Lisboa 2020), under the PORTUGAL 2020 Partnership Agreement through the European Regional Development Fund (ERDF) and Fundação para a Ciência e Tecnologia (Portugal), project LISBOA-01-0145-FEDER-022170.

References

1. Veraart et al. Diffusion MRI noise mapping using random matrix theory. Magn Reson Med. 2016

2. Veraart et al. Denoising of diffusion MRI using random matrix theory. NeuroImage. 2016

3. Lemberskiy et al. Achieving sub-mm clinical diffusion MRI resolution by removing noise during reconstruction using random matrix theory. ISMRM proceedings. 2019

4. Cordero-Grande et al. Complex diffusion-weighted image estimation via matrix recovery under general noise models. NeuroImage. 2019

5. Does et al. Evaluation of principal component analysis image denoising on multi-exponential MRI relaxometry. Magn Reson Med. 2019

6. Zhao et al. Detail-Preserving Image Denoising via Adaptive Clustering and Progressive PCA Thresholding. IEEE Acess. 2018

7. Brender et al. Dynamic Imaging of Glucose and Lactate Metabolism by 13 C-MRS without Hyperpolarization. Scientific Reports. 2019

8. Gavish et al. Optimal Shrinkage of Singular Values. IEEE Trans Inf Theory. 2017

9. Veraart et al. TE dependent Diffusion Imaging (TEdDI) distinguishes between compartmental T2 relaxation times. NeuroImage. 2018

10. Lampinen et al. Towards unconstrained compartment modeling in white matter using diffusion-relaxation MRI with tensor-valued diffusion encoding. Magn Reson Med. 2020

11. Kleban et al. Strong diffusion gradients allow the separation of intra- and extra-axonal gradient-echo signals in the human brain. NeuroImage. 2020

12. Shemesh and Jespersen et al. Conventions and nomenclature for double diffusion encoding NMR and MRI. Magn Reson Med. 2015

Figures

Figure 1. Visualization of tensor MP-PCA algorithm for three-index patches. Illustrates the steps in the tensor MP-PCA algorithm provided under Theory. The illustration introduces $$$p_1$$$ as the number of signal components identified in the $$$n=1$$$ MP rank-reduction step. The three vertical dots at the bottom signifies that the algorithm reiterates through the steps above with the $$$i_2$$$-flattening of $$$\tilde{X}_1$$$.

Figure 2. Denoising performance on acquired data. Left: comparison of data before and after applying tensor MP-PCA for the highest and lowest SNR scenarios. A typical 5x5x5 sliding window was used. Right: squared residual distributions. Dashed lines are Gaussian references, showing that the removed variance is approximately Gaussian. The residuals are scaled relative to those of matrix MP-PCA, showing that tensor MP-PCA removes 24% more noise in these data.

Figure 3. SNR gain as a function of window width for multi-TE phantom data. Left/right panel: denoising performance with a 2D/3D sliding window. Tensor MP-PCA reaches higher performance and at smaller window size. The relative SNR after denoising is calculated from the RMSE between the denoised and ground truth brain signal, normalized to the simulated noise $$$\sigma$$$. Note that without denoising, the RMSE equals $$$\sigma$$$ resulting in relative SNR = 1.

Figure 4. SNR gain as a function of window width for single-TE phantom data. Left/right panel: denoising performance with a 2D/3D sliding window. Tensor MP-PCA reaches higher performance and at smaller window size, but the improvement is smaller than for multi-TI phantom data (Fig. 2). The relative SNR after denoising is calculated from the RMSE between the denoised and ground truth brain signal, normalized to the simulated noise $$$\sigma$$$.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

2905

DOI: https://doi.org/10.58530/2022/2905