2869
Inter-coil applicability of trained neural networks for B1+ prediction in parallel-transmit.1Cardiff University, Cardiff, United Kingdom
Synopsis
Motion-resolved parallel-transmit (pTx) B1-maps can be predicted using neural networks, facilitating online pulse re-design – a prospective solution to motion. However, networks require large training-datasets. Since different pTx coils inherently produce different B1-distributions, it is unclear whether coil-specific training-datasets are needed. Here, we train networks on simulated data from one coil-model and test on 6 differently-sized coil-models. While performance was optimal for the coil on which networks were trained, B1-prediction yielded lower error than that caused by motion in ≥91% of magnitude, and ≥55% of phase evaluations for 5 out of the 6 models, demonstrating some generalisability across coils.
Background
B1+ fields are sensitive to head motion, which causes artificial contrast when pulses are applied - especially in pTx where channels’ interference patterns change1-4. To prevent this, motion-resolved B1-maps can be predicted using deep learning5,6. Predicted maps can then be used for online pulse re-design7, thereby compensating the effects of motion on B1+ prospectively.A recent study proposed a method for B1-prediction using deep neural networks5. The method used simulated data from one coil model to train and test networks. Here, we investigate whether minor variations in pTx coil design necessitates retraining such networks. To do this, we train networks using data simulated with one pTx coil model, and test them on data from 5 additional, differently-sized pTx coil models.
Methods
Billie, Duke and Ella of the Virtual Population8 were simulated at 7T with Sim4Life (Zurich MedTech, Zurich) at 20 different head positions, and using 6 different coil models (figure 1). Coils A-F ranged in loop height and width (and/or array radius) by ±25% of the base model (coil-C). Billie and Duke models (with coil-C) were used to train networks, while Ella (with all coil models) was used for testing.Conditional generative adversarial networks (cGANs)9 were trained for a set of discretized head movements to cover the axial plane. Networks took ~6 hours to train using a DGX-1 NVIDIA GPU. Training and evaluation parameters and routines followed those described in5.
Error (nRMSE for magnitude, L1 for phase) and voxel-wise correlation coefficient were calculated between firstly, the centre and displaced simulated maps, to quantify the impact of motion, and secondly, the network-predicted and displaced simulated maps, to quantify prediction quality. The two were compared to assess the benefits of B1-prediction. Prediction quality across coil models compared to that for coil-C (which networks were trained on) was of primary interest. Pair-wise one-way ANOVAs between coils were conducted to assist this comparison.
Finally, to evaluate practical benefits of pulse re-design using predicted maps, pTx pulses were designed10,11 using centred and predicted maps, and evaluated on the ground-truth displaced map.
Results
Figure 2 shows maps for 2 example displacements. Motion-related error was qualitatively similar across coils A-E, while prediction error varied somewhat. Nevertheless, the reduction of motion-induced error in all except coil-F is clear.Figure 3 shows error averaged over all evaluations for a given coil/displacement. Coil-C yielded significantly lower magnitude prediction error (mean = 6.4%) than all other coils (means between 8.4 - 9.7%). Coils A-E benefitted from predicted maps, as seen by the similar divergence of predicted and motion-related errors. On the other hand, error in predicted maps for coil-F often exceeded motion-related error, especially for phase.
Figure 4 shows worst-case observations across all metrics. Magnitude nRMSE was higher for the smaller coil models (coil-B = 124%), but for all coils, the highest-observed prediction error was still lower than the highest motion-related error (fig. 4a). As expected, coil-C experienced the lowest worst-case magnitude prediction error (33%). The widest/longest-looped and narrower-looped coils had the highest (F = 63%) and second-highest (A = 56%) prediction errors, respectively. Coils B-E all had worst-cases below 46%, resulting in a U-shaped relationship between coil size and worst-case nRMSE.
Similarly, minimum-observed magnitude correlation due to motion was lowest for the narrower-looped coil (coil-A = 0.82; fig. 4c), whereas predicted maps correlated most strongly with ground-truth maps for coil-C (0.98). Prediction correlations remained high (≥0.97) for coils B-E. Overall, prediction correlation for coils A and F were significantly lower than coil-C.
For phase, the mid-large coils (C-E) suffered most following motion, and also yielded the highest worst-cases in predictions (fig. 4b & 4d). Unexpectedly, coil-C yielded the highest-observed phase error. Despite this, the mean phase error for coil-C (7.1°) was significantly lower than all others except for coil-B (which was 7.4°). Mean prediction correlation did not significantly differ between coils.
Figure 5 shows flip-angle results for pulses designed using centre (simulated) and predicted maps.
Discussion
B1-prediction for coils with the same loop width but longer/shorter loops was superior to coils with narrower/wider loops of the same length. Prediction performance was worst for the coil that had wider and longer loops, and larger array radius (unsurprising, since this was the most dissimilar structure).Even though motion-related error was larger for smaller coils and lowest for the largest coil array, networks yielded much better performance in suppressing error in the former case, which we attribute to the similarity in coil structures.
Although most coils benefitted from B1-prediction, performance for the coil on which networks were trained was statistically better as expected. A potential alternative to fully pre-trained networks may be to fine-tune coil-specific networks via transfer learning12 with a small, coil-specific training dataset.
Further research could explore different coil configurations and test these findings experimentally.
Conclusion
Although the largest coil model, which had a 25% larger array radius, did not reliably benefit from the trained networks, coils A-E (which had smaller/larger loops, but the same array radius as the coil used for network training) benefitted in at least 91% of magnitude, and at least 55% of phase evaluations. Therefore, minor variations in coil design may not require re-training networks, simplifying adoption of the motion-correction framework outlined in (5).Acknowledgements
No acknowledgement found.References
1. Kopanoglu E, Deniz CM, Erturk MA, Wise RG. Specific absorption rate implications of within‐scan patient head motion for ultra‐high field MRI. Magnetic Resonance in Medicine 2020.
2. Kopanoglu E, Plumley A, Erturk MA, Deniz C, Wise R. Implications of within-scan patient head motion on B1+ homogeneity and Specific Absorption Rate at 7T. Proc Intl Soc Mag Reson Med 27 2019.
3. Ajanovic AH, Joseph; Tomi-Tricot; Raphael, Malik, Shaihan. Motion and Pose Variability of SAR Estimation with Parallel Transmission at 7T. 2021. p 2487.
4. Plumley A, Schmid P, Kopanoglu E. Parallel-transmit coil dimensions affect SAR sensitivity to motion at 7T. Proc Intl Soc Mag Reson Med 29 2021:2315.
5. Plumley A, Watkins L, Murphy K, Kopanoglu E. Motion-resolved B1-prediction using deep learning for real-time pTx pulse-design. Proc Intl Soc Mag Reson Med 29 2021:0223.
6. Abbasi‐Rad S, O’Brien K, Kelly S, Vegh V, Rodell A, Tesiram Y, Jin J, Barth M, Bollmann S. Improving FLAIR SAR efficiency at 7T by adaptive tailoring of adiabatic pulse power through deep learning estimation. Magnetic Resonance in Medicine 2020.
7. Kopanoglu E. Near real-time parallel-transmit pulse design. Proceedings of the 26th ISMRM 2018:3392.
8. Gosselin M-C, Neufeld E, Moser H, Huber E, Farcito S, Gerber L, Jedensjö M, Hilber I, Gennaro FD, Lloyd B, et al. Development of a new generation of high-resolution anatomical models for medical device evaluation: the Virtual Population 3.0. Physics in Medicine & Biology 2014;59(18):5287–5303-5287–5303.
9. Isola P, Zhu J-Y, Zhou T, Efros AA. Image-to-Image Translation with Conditional Adversarial Networks. CoRR 2016;abs/1611.07004.
10. Grissom W, Yip C-Y, Zhang Z, Stenger VA, Fessler JA, Noll DC. Spatial domain method for the design of RF pulses in multicoil parallel excitation. Magnetic Resonance in Medicine 2006;56(3):620–629-620–629.
11. Kopanoglu E, Constable RT. Radiofrequency pulse design using nonlinear gradient magnetic fields. Magnetic Resonance in Medicine 2015;74(3):826–839-826–839.
12. Fregier Y, Gouray J-B. Mind2Mind: transfer learning for GANs. International Conference on Geometric Science of Information. Volume arXiv:1906.116132021.
Figures
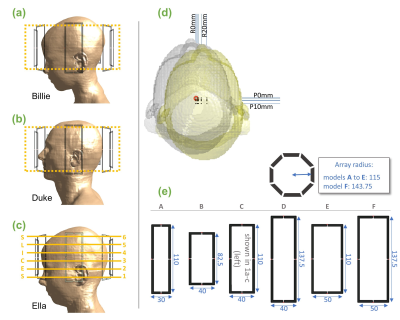
Fig.1 Slices from a slab (shown in yellow) from Billie (a) and Duke (b) body models were used to train networks with 1 coil model. Networks were tested using Ella (c) at the 6 indicated slices. Testing was conducted with differently-sized coil models shown in (e). (d) positions simulated for each model. Positions covered an axial grid at 0,2,5,10,20mm right and 0,2,5,10mm posterior. (e) Coil models A-F. One loop from each pTx array is shown (dimensions in mm). Coil-C was used to train networks.
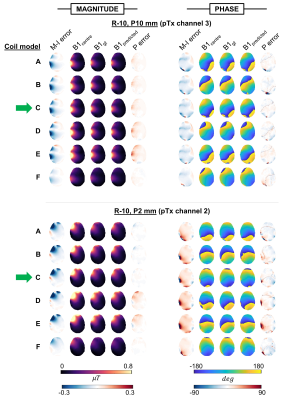
Fig.2 B1+ magnitude and phase maps for 2 example displacements rightward(a single pTx channel is shown). B1centre is the simulated map without motion (network inputs). B1gt is the ground-truth simulated map at the displaced position, and B1predicted is the network-output map (at the same displaced position). Motion-induced (M-I) error shows difference between B1initial and B1gt. Prediction (P) error shows difference between predicted and ground truth maps. Networks were trained using coil-C (green arrow).
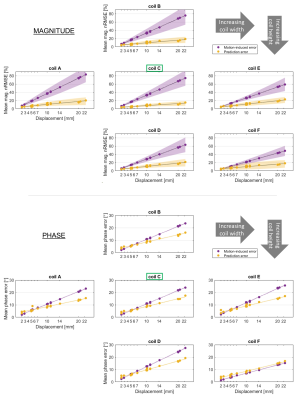
Fig.3 Mean magnitude (a) and phase (b) error, averaged across all slices and channels for each displacement. Motion- and prediction-related errors are shown in purple and yellow, respectively. Different coil models (with varying loop size and/or array radius - see figure 1e) are shown in subplots. Networks were trained for coil-C, indicated with green boxes. Magnitude nRMSE is shown as % of the mean magnitude without motion. Standard deviation is shown for magnitude (shaded regions) but omitted from phase for clarity.
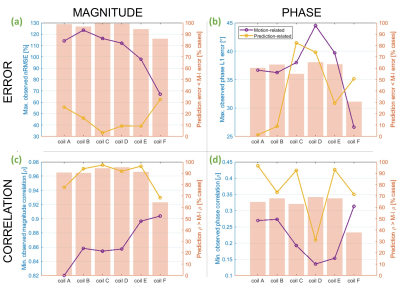
Fig.4 Motion-induced (purple) and prediction-related (yellow) error and correlation coefficient for magnitude (a & c) and phase (b & d). These are worst-observed cases across all evaluations for each coil model. The left-hand axis pertains to these line plots. Bar charts (with right-hand y axis) show the percentage of evaluations for which prediction-related error was lower (or correlation was higher) than that caused by motion. Networks were trained using data from coil-C only.
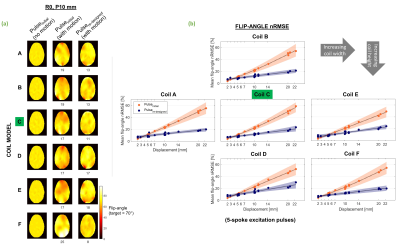
Fig.5 (a) Example flip-angle profiles. Pulseinitial was designed conventionally, using the B1-map without motion. Its performance following a 10mm posterior displacement is shown in the middle column. Pulsere-designed was designed using predicted maps and evaluated on the same displaced map. nRMSE (%) for both pulses following motion is shown below profiles (b) Flip-angle nRMSE for both pulses, averaged over all slices for each displacement. Orange and purple show performance of pulseinitial and pulsere-designed, respectively. nRMSE is % of target flip-angle (70°).