2866
Improved B1+- and resonance offset-robust slice-selective inversion pulses
Christina Graf1, Adam Berrington2, Martin Soellradl1, Armin Rund3, and Rudolf Stollberger1
1Institute of Medical Engineering, Graz University of Technology, Graz, Austria, 2Sir Peter Mansfield Imaging Centre, School of Physics and Astronomy, University of Nottingham, Nottingham, United Kingdom, 3Institute for Mathematics and Scientific Computing, University of Graz, Graz, Austria
1Institute of Medical Engineering, Graz University of Technology, Graz, Austria, 2Sir Peter Mansfield Imaging Centre, School of Physics and Astronomy, University of Nottingham, Nottingham, United Kingdom, 3Institute for Mathematics and Scientific Computing, University of Graz, Graz, Austria
Synopsis
In this work, an optimal control framework and its application for the development and improvement of $$$B_1^+-$$$ and $$$\Delta B_0-$$$robust, slice-selective inversion pulses is introduced. The optimized RF pulse shows superior performance compared to adiabatic, state of the art pulses through simulations, phantom experiments, and in vivo measurements. Measurements on a 3T MR system revealed improved slice-profile quality of the optimized pulse, especially for low $$$B_1^+$$$ and high $$$\Delta B_0$$$. Since the performance is independent of the field strength, its application in ultrahigh-field spectroscopy seems straightforward.
Introduction
$$$\Delta B_0-$$$ and $$$B_1^+-$$$robust, slice-selective $$$180^\circ$$$ pulses are required in several MR applications, such as in high-field MR spectroscopy for robust localization. Various gradient-modulated adiabatic RF pulses fulfill the requirement of $$$B_1^+-$$$robustness to some extent. However, for off-resonant spins ($$$\Delta B_0-$$$inhomogeneities, chemical shift) a degradation (or `smearing') of the slice-profile is observed, particularly within regions of low $$$B_1^+$$$. Parameters of specific adiabatic pulses have been optimized to improve for robustness1,2. However, this restricts the solution to selected functions. In this work, slice-selective, $$$B_1^+-$$$ and $$$\Delta B_0-$$$robust $$$180^\circ$$$ pulses are designed with variable waveforms by using optimal control3. By jointly optimizing the RF and gradient-waveform within given bounds, the proposed framework allows improved slice-profile quality at low $$$B_1^+$$$ and high $$$\Delta B_0$$$. The optimized inversion pulse is validated in phantom and in vivo measurements on a 3T MRI system.Theory
A desired slice-profile, $$$M_{d}$$$, shall be achieved at the end of the slice-selective inversion pulse. A uniform discretization of $$$B_1^+-$$$scalings and $$$\Delta B_0-$$$offsets resulting in $$$N_{B_1^+}$$$ and $$$N_{\Delta B_0}$$$ steps is applied. The average magnetization profile over all $$$\Delta B_0-$$$offsets is defined as$$\widetilde{M}_{i}(z,t)=\frac{1}{N_{\Delta B_0}}\sum\limits_{j=1}^{N_{\Delta B_0}}M_{i,j}(z,t),\quad\forall i=1,\cdots N_{B_1^+}.$$
An ensemble cost functional3 for controlling the RF pulse waveform, $$$B_1^+$$$, and the slice-selective gradient waveform, $$$G_s$$$, is given as
$$\underset{(B_1^+, G_s)}{\min}J=\varepsilon+\frac{\alpha}{2}\int\limits_{0}^{T}(B_1^{+2}+G_s^2)dt\\ \text{s.t.}\begin{cases}\left|\widetilde{M}_{i}(T,z)-M_d(z)\right|<\varepsilon\quad\forall i=1,\cdots N_{B_1^+},\quad\forall z\in\Omega\\0\leq B_1^+\leq B_{1,max}^+,\quad G_{s,min}\leq G_s\leq G_{s,max}\\ \frac{d M_{ij}}{dt}=\gamma B_{ij}\times M_{ij}+b,\quad M_{ij}(0)=M^0,\quad\forall i=1,\cdots N_{B_1^+},\,j=1,\cdots N_{\Delta B_0}\end{cases}$$
$$$\varepsilon$$$ defines the allowed distance from the target magnetization, the latter term in the cost functional reduces the pulse energy. The Bloch equations and their adjoint equations are solved using a symmetric operator splitting4 and exact discrete derivatives were assured. The optimization itself is based on a trust-region semi-smooth quasi-Newton method5,6.
Methods
The above described cost functional was implemented in MATLAB (The Mathworks Inc, Natick, USA). The desired state was a rectangular slice with thickness $$$2cm$$$ over spatial domain $$$\Omega=\pm10cm$$$. $$$B_1^+-$$$robustness was required for scales $$$(70\%-130\%)$$$ in $$$N_{B_1^+}=7$$$ steps. $$$\Delta B_0-$$$robustness was demanded for $$$\pm600$$$ Hz in $$$N_{\Delta B_0}=81$$$ steps. A slice-selective GOIA-WURST(16,4) pulse7 (GOIA) was used to initialize optimization. Numerical validation of the optimized pulse (OPTIM) and original GOIA was determined using the maximum deviation from the desired profile for each pair $$$B_1^+ / \Delta B_0$$$.GOIA and OPTIM were implement on a 3T MR system (Magnetom Vida, Siemens Healthcare, Erlangen, Germany) as preparation pulses within a spoiled gradient-echo sequence. Phantom measurements using a cylindrical MR phantom ($$$T_1=102ms$$$, $$$T_2=81ms$$$) were performed. The sequence parameters were set to $$$TE/TR=3.14/500ms$$$, $$$FOV=150\times150mm$$$, resolution $$$0.8 \times0.8\times5mm$$$, flip angle $$$90^\circ$$$. To measure the effect of $$$B_1^+-$$$variations on the slice-profile, we varied the transmit voltage of the scanner up to $$$\pm30\%$$$, and variations in $$$\Delta B_0$$$ were achieved by shifting the carrier frequency over $$$\pm500Hz$$$. A Siemens 18 channel transmit and receive knee coil was used. Furthermore, brain images of a healthy subject with both inversion pulses were acquired using a Siemens 20-channel receive-array head coil ($$$TE/TR=3.14/3000ms$$$, $$$FOV=230\times230mm$$$, resolution $$$1.8\times1.8\times5mm$$$, flip angle $$$90^\circ$$$).
Results and Discussion
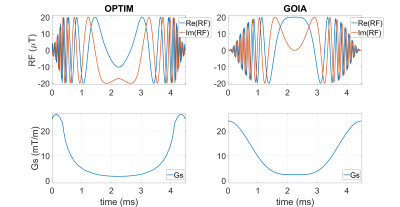
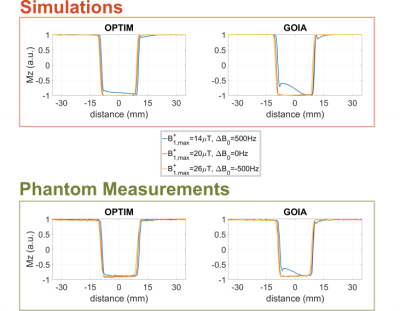
The proposed optimization framework resulted in modified RF and slice-selective gradient waveforms of OPTIM compared to GOIA (Fig. 1), while fulfilling amplitude and slew rate restrictions on the RF and gradient systems.For higher RF amplitudes, in simulations and phantom measurements, all profiles were comparable between OPTIM and GOIA (Fig. 2). However, for low $$$B_1^+$$$ and a high resonance offset, OPTIM performs significantly better. Here, GOIA showed only $$$75\%$$$ inversion efficiency in the slice which could be improved to $$$93\%$$$ using OPTIM.
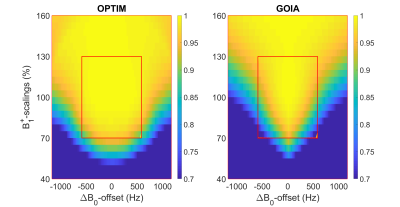
The effect of all simulated $$$\Delta B_0-$$$ and $$$B_1^+-$$$combinations is shown in Fig. 3. GOIA lacked performance for low $$$B_1^+$$$ and higher $$$\Delta B_0$$$ values with an efficiency of less than $$$90\%$$$. OPTIM shows an almost evenly distributed performance over the optimized domain with an excellent inversion efficiency in the center of the box and still acceptable performance at the bottom corners. But also outside of the explicitly optimized range, especially for a $$$B_1^+-$$$scale of $$$130\%$$$ and more, the efficiency of OPTIM reaches still top values with $$$98\%$$$.
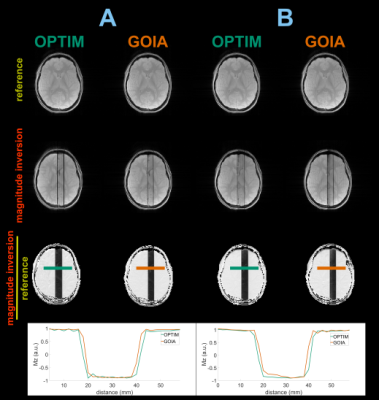
For in vivo (Fig. 4), in case (A) both RF pulses depict a distinct slice-profile and an efficiency of $$$85\%$$$. In case (B), OPTIM shows an efficiency of $$$85\%$$$, whereas GOIA only resulted in $$$70\%$$$. In addition, off-resonant smearing can be observed as a non-uniform inversion in the images. A proposed clear application of OPTIM is for ultra-high field MRS, where off resonant slices are positioned at around $$$\pm 600Hz$$$.
Conclusion
We optimized slice-selective, $$$\Delta B_0-$$$ and $$$B_1^+-$$$robust inversion pulses by optimal control. We demonstrated in simulations, phantom and in-vivo measurements an excellent slice-profile quality even when resonance offsets and $$$B_1^+-$$$inhomogeneities are present. Pulse design based on optimal control enables a distinct improvement of the already robust $$$180^\circ$$$ adiabatic selective pulses, especially for low $$$B_1^+$$$ and high $$$\Delta B_0$$$. Therefore, these pulses may be particularly advantageous for MRS at $$$7T$$$ and more to maintain off-resonant slice-profile with a low or variable $$$B_1^+$$$.Acknowledgements
No acknowledgement found.References
1Berrington A, Gillen J.S, Boer V. GOIA-WURST optimisation for ultra-high field single-voxel MRS at short-TE. In Proceedings of the International Society of Magnetic Resonance in Medicine (ISMRM), 2021.
2Wang K, Shao X, Yan L, Ma S.J, Jin J, Wang S.J.J. Optimization of adiabatic pulses for pulsed arterial spin labeling at 7 tesla: Comparison with pseudo-continuous arterial spin labeling. Magn Reson Med 2021;85:3277-3240.
3Graf C, Soellradl M, Aigner C.S, Rund A, Stollberger R. Time optimal control based design of robust inversion pulses. In Proceedings of the International Society of Magnetic Resonance in Medicine (ISMRM), 2021.
4Graf C, Rund A, Aigner C.S, Stollberger R. Accuracy and Performance Analysis for Bloch and Bloch-McConnell simulation Methods. J Magn Reson 2021;329:107011.
5Rund A, Aigner C.S, Kunisch K, Stollberger R. Magnetic Resonance RF Pulse Design by Optimal Control with Physical Constraints. IEEE Trans Med Imaging 2018;37:461-472.
6Mannel F, Rund A. A Hybrid Semismooth Quasi-Newton Method for nonsmooth Optimal Control with PDEs. Optim Eng (2020).
7Tannus A, Garwood M. Adiabatic Pulses. NMR Biomed, vol. 10, pp.424-434, 1997.
Figures
RF pulse shapes (top) with corresponding slice-selective gradient shapes (Gs) (bottom) of OPTIM (left) and the initial GOIA RF pulse (right). Both pulses have a duration of $$$T=4.5ms$$$, a maximum amplitude of the RF of $$$20\mu T$$$ for both, a maximum gradient amplitude of $$$26.6 / 24 mT/m$$$, and a normalized power integral of $$$3.99/3.35$$$ for OPTIM / GOIA.
Simulation (top) and phantom measurement (bottom) inversion profiles for OPTIM (left) and GOIA (right), whereby the measurement was done using a cylindrical MR phantom. Depicted are three combinations of a maximum $$$B_1^+-$$$amplitude and offset $$$\Delta B_0$$$.
Performance for OPTIM and GOIA for various combinations of $$$B_1^+-$$$scalings and $$$\Delta B_0-$$$offsets, the efficiency was calculated as 1 - maximum deviation. The efficiency scale reaches from $$$70\%$$$ to $$$100\%$$$. The red box indicates the area where OPTIM was optimized.
In vivo measurement at $$$B_1^+=100\%$$$ and $$$\Delta B_0=0Hz$$$ (A), and $$$B_1^+=75\%$$$ and $$$\Delta B_0=500Hz$$$ (B). Reference image without inversion pulses (line 1), magnitude of the measurements with the inversion pulses (line 2) and the inversion, i.e. the magnitude of the inversion image divided by the reference image (line 3). Inversion profile on a distinct line (line 4). The left columns depict OPTIM, the right the GOIA.
DOI: https://doi.org/10.58530/2022/2866