Introduction

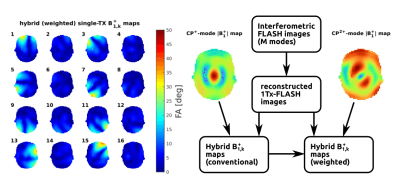
With a growing number of transmit (Tx) channels in Ultra-High Field (UHF) MRI the need for fast, accurate and low-SAR mapping of Tx RF-field ($$$B_1^+$$$) becomes increasingly important. Considering $$$K$$$ transmit coils $$$k$$$, the field $$$B_{1,k}^+$$$ of each transmitter consists of the magnitude $$$|B_{1,k}^+|$$$ and its phase $$$\varphi_k$$$ and is given by $$$B_{1,k}^+=|B_{1,k}^+|\cdot\,e^{i\varphi_k}$$$. For any arbitrary RF mode $$$\vec{m}=(m_0\cdot\,e^{i\varphi_0},\cdots,m_K\cdot\,e^{i\varphi_K})^T$$$ the resulting $$$B_1^+$$$ field will be $$$B_{1,m}^+=\sum_{k=1}^{K} B_{1,k}^+\cdot\,m_k$$$. Note that knowledge of the elements' phase relative to each other is sufficient for arbitrary combinations.
Since the $$$B_1^+$$$ distribution of individual transmit channels often varies beyond the dynamic range of the mapping method, interferometric mapping¹ is often used. In this, a set of $$$M$$$ RF modes $$$I$$$ is applied, with $$$i_{m,k}$$$ as the m-th mode and the k-th Tx element, resulting in a $$$B_1^+$$$ map subject to the RF mode: $$$B_{1,m}^+$$$. From the $$$M$$$ $$$B_1^+$$$ maps, individual $$$B_{1,k}^+$$$ fields can be determined pixel-by-pixel:
$$B_{1,k}^+(r)=\sum_{m=1}^M(I^{-1})_{m,k}\cdot\,B_{1,m}^+(r)$$
Furthermore, to expedite $$$B_1^+$$$ mapping, hybrid $$$B_1^+$$$ mapping² can be applied. Under the assumption that received signal $$$|S(r)|\propto\alpha$$$, single transmit FLASH images (also called "relative $$$B_1^+$$$ maps") $$$S_k$$$ can be summed up to the combined image: $$$S(r)\approx\sum_{k=1}^{K}S_k(r)$$$. The same assumption allows to determine individual Tx $$$B_1^+$$$ maps:
$$|B_{1,k}^+(r)|=\{|S_k(r)|\div\,|S(r)|\}\cdot\,|B_1^+(r)|$$

In this work a saturated TurboFLASH sequence (SatTFL³) was used to acquire 3D $$$|B_1^+|$$$ maps, while $$$\varphi$$$ of any given mode $$$m$$$ was taken from unprepared FLASH images $$$S_m$$$. The performance of several interferometry patterns was compared. Interferometry was combined with hybrid $$$B_1^+$$$ mapping in order to reduce measurement time. Additionally, a second $$$|B_1^+|$$$ map was introduced to hybrid imaging in an attempt to increase hybrid mapping accuracy without increasing the required scan time too much.

Methods

All measurements were performed on a 9.4T whole-body MRI scanner (Magnetom 9.4T Plus, Siemens Healthineers, Germany) with 16 independent transmit channels, a custom built head coil (16Tx, 31Rx)⁴ and a head-shaped agar phantom (T1=2.6s).

SatTFL $$$B_1^+$$$ mapping
SatTFL $$$B_1^+$$$ mapping was done with a 3D FLASH sequence with a rectangular preparaion pulse and strong spoiler gradients after preparation (TR=2.50ms, TE=0.73ms, BW=1000 Hz/Px, asymmetric echo, elliptical k-space acquisition, GRAPPA 2×2, FA readout=1°, FA presaturation=60°, 795 k-space lines, readout duration=1.988s, presat pulse duration=500µs, matrix size=64$$$^3$$$, resolution=3.5mm isotropic, pause between absolute maps=10s, pause between FLASH images=0.5s).

Interferometric $$$B_1^+$$$ mapping
Several sets of RF modes were used for interferometric $$$B_{1,k}^+$$$ mapping.
For determining mapping performance, $$$|B_1^+|$$$ maps of 9 randomly selected RF-modes were recorded ($$$|{B_1^+}_{ref}|$$$). The same RF-modes were applied to the measured $$$B_{1,k}^+$$$ maps and the root mean square error (RMSE) was calculated as measure for mapping accuracy.

The interferometry modes applied were (with $$$h_{n,k}$$$ being the n/k-th element of a Hadamard-matrix $$$H$$$ of order $$$M$$$ and $$$\delta_{n,k}$$$ being the Kronecker-delta):
One On: $$$i_{n,k}=\delta_{n k}$$$; One Off: $$$i_{n,k}=1-\delta_{n k}$$$; One Inv: $$$i_{n,k}=1\cdot(-1\cdot\delta_{n k})$$$; Phase-cycling: $$$i_{n,k}=1\cdot\,exp({i\cdot\,360^{\circ}\div{N}\cdot(n-1)\cdot\,m})$$$; Hadamard Amplitude: $$$i_{n,k}=h_{n,k}$$$; Hadamard Phase: $$$i_{n,k}=1\cdot\,exp(i\cdot\,180^{\circ}\cdot\,h_{n,k})$$$;

Hybrid $$$B_1^+$$$ mapping
Hybrid $$$B_1^+$$$ mapping was implemented by reconstructing single-Tx signals $$$S_k$$$ from the modes' signals $$$S_m$$$ before estimating $$$B_{1,k}^+$$$.
In an attempt to increase accuracy, a second absolute $$$B_{1,m}^+$$$ map was introduced with an additional phase shim (here $$$CP^{2+}$$$) and the corresponding $$$S_{k,m}$$$ maps were constructed by applying said phase shift to the $$$S_k$$$ images. The conversion from $$$S_k$$$ and $$$S_{k,m}$$$ to $$$B_{1,k}^+$$$ was done by weighted combination:
$$
|B_{1,k}^+(r)|=\frac{|S_k(r)|}{|S(r)|}\cdot|B_1^+(r)|\cdot\frac{|S_(r)|}{|S(r)|+|S_m(r)|}+\frac{|S_{m,k}(r)|}{|S_m(r)|}\cdot|B_{1,m}^+(r)|\cdot\frac{|S_m(r)|}{|S(r)|+|S_m(r)|}
$$

The resulting $$$B_{1,k}^+$$$ maps were tested against the randomly chosen $$${B_1^+}_{ref}$$$ maps by applying the same RF-modes to them.

Results

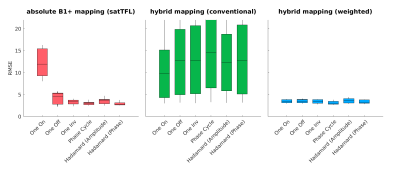
Fig. 1 displays the RMSEs of the $$$|B_{1,m}^+|$$$ maps calculated from the different interferometry modes and $$$B_1^+$$$ mapping methods compared to their corresponding measured maps $$$|B_{1,m}^+|$$$.
It can be seen that the different sets of interferometry modes vary greatly in performance. As expected, the One On mode performed worst (RMSEs: 8.01° .. 16.29°). The lowest RMSEs were achieved by phase-cycling (2.46° .. 3.84°), followed by the Hadamard phase modes (2.53° .. 3.76°)
Conventional hybrid mapping resulted in average RMSEs over 10° for all interferometry mode sets. Introducing a second $$$|B_1^+|$$$ map as reference (weighted hybrid mapping) improved performance greatly (RMSEs in phase-cycling: 2.66° .. 3.83°).
The total recording times for interferometric mapping, conventional hybrid mapping and weighted hybrid mapping were 244s, 64s and 76s respectively.

Discussion

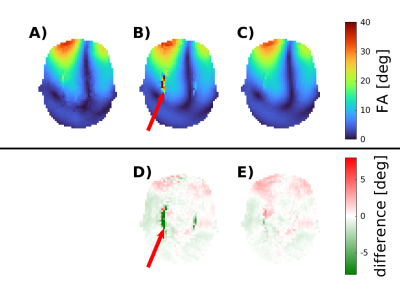
This study shows that $$$B_1^+$$$ Interferometry has huge advantages for multi-channel $$$B_1^+$$$ mapping. Conventional hybrid mapping delivered very poor results. A possible explanation for this finding is that $$$B_1^+$$$ inhomogeneities are very strong at 9.4T, which causes the $$$B_1^+$$$ distribution in the phantom to exceed the usable dynamic range of the sequence.
By introducing a second $$$|B_1^+|$$$ map, the accuracy of hybrid mapping increased tremendously. However, hybrid mapping still could not match the performance of intrerferometric satTFL $$$B_1^+$$$ mapping.

Since $$$B_1^+$$$ inhomogeneities in-vivo tend to be lower than in the phantom used for this study, it can be expected that the weighted hybrid maps perform comparably well for in-vivo applications. Due to its extremely short acquisition time there is great potential in weighted hybrid $$$B_1^+$$$ mapping, which is why this study should be followed up by in-vivo experiments.

Experiments at different UHF field strengths, which share the difficulty of having to cope with strong $$$B_1^+$$$ inhomogeneities, are necessary to investigate how strongly the performance of the selected interferometry modes depends on $$$B_0$$$.

Acknowledgements

This project was sponsored by the Deutsche Forschungsgemeinschaft (DFG – German Research Foundation) under the Reinhart Koselleck Programme (DFG SCHE 658/12)