2862
T2 measured with multiple spin-echo depends on echo spacing as well as orientation1UBC MRI Research Centre, Vancouver, BC, Canada, 2Physics & Astronomy, University of British Columbia, Vancouver, BC, Canada, 3Institute for Physical Chemistry, Albert-Ludwigs-University, Freiburg, Germany, 4Radiology, University of British Columbia, Vancouver, BC, Canada, 5Pediatrics, University of British Columbia, Vancouver, BC, Canada
Synopsis
The MRI signal in white matter tissue is composed of constituent signals from two different water pools: intra/extracellular water and myelin water. When using a multi spin-echo acquisition, the relaxation rate measured in each pool has been shown to depend on the orientation of the containing white matter fibre with respect to the main magnetic field. Here, we show an additional influence of the acquisition echo spacing on the apparent intra/extracellular rate relaxation rate, and using numerical simulation, we provide evidence that decoherence mediated by diffusion through local field inhomogeneities created by blood vessels cannot explain the observed orientation dependence.
Introduction
The orientation dependence of the transverse relaxation time $$$R_2=1/T_2$$$ in white matter (WM) as measured with multi spin-echo (MSE) MRI is commonly attributed to diffusion through magnetic field inhomogeneities created by the diamagnetic myelin sheaths surrounding the axons1–5. It has also been shown that diffusion through inhomogeneities due to WM vasculature generates an orientation dependence in spin-echo dynamic susceptibility contrast (SE-DSC) MRI6. In both cases, the field inhomogeneities and therefore the diffusion-mediated loss of coherence depends on the angle $$$\theta$$$ between the axons (or blood vessels) and the main magnetic field of the scanner. Simulations of a model system for white matter - a set of parallel hollow diamagnetic cylinders - predict an orientation-dependence of the relaxation rate as7 $$R_2(\theta)=R_{2,\text{iso}}+R_{2,\text{aniso}}\sin^4\theta,$$ where $$$R_{2,\text{aniso}}$$$ depends on the diffusivity $$$D$$$. This dependence stems from the fact that diffusion-mediated decoherence increases as the characteristic diffusion length $$$d\propto\sqrt{D}$$$ increases, as spins will sample larger regions of field inhomogeneities.To investigate the degree to which diffusion contributes to the observed orientation dependence of $$$R_2$$$, we varied the echo spacing (TE) of the MSE acquisition. Variation of echo spacing modifies the effect of diffusion, since the distance travelled by diffusing spins between $$$180^{\circ}$$$ refocusing pulses decreases with decreasing echo spacing. This results in phase accumulation within approximately homogeneous local fields, allowing the spin magnetization to be partially refocused. As the echo spacing increases, however, diffusing spins will travel further and sample larger regions of inhomogeneous field, decreasing the ability of refocusing pulses to compensate for diffusive signal loss.
Methods
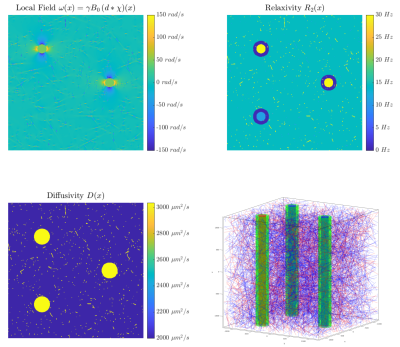
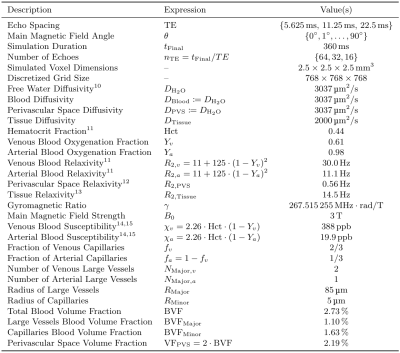
Seven healthy volunteers were scanned at 3T. Carr-Purcell-Meiboom-Gill (CPMG) MSE sequences were acquired for five different echo spacings ($$$\text{TE}=6,8,9.6,12,16$$$ms; $$$\text{TR}=1500$$$ms; reconstructed voxel size=$$$1.797\times1.797\times1.8\,\text{mm}^3$$$; matrix size=$$$128\times128\times67$$$). To enforce constant effective TR, the number of echos (nTE) was adjusted such that the echo train length was fixed to 288 ms ($$$\text{nTE}=48,36,30,24,18$$$). Diffusion tensor imaging (DTI) was used to map local fibre orientation. DECAES8 was used to decompose the signal into $$$T_2$$$ components. The allowed $$$T_2$$$ components $$$\mathcal{T}=\left\{T_2^j\right\}_{j=1}^{40}$$$ were logarithmically spaced between $$$6\text{ms}$$$ and $$$1\text{s}$$$. For each scan, the subset $$$\left\{T_2\in\mathcal{T}\,\vert\,\text{TE}\le{}T_2\le{}1\text{s}\right\}$$$ of values were used to avoid overfitting to $$$T_2$$$ components shorter than TE. A cutoff of 25ms was chosen to differentiate between fast relaxing myelin water (MW) components and the slower intra/extracellular water (IEW). As the myelin water signal is sensitive to TE, our analysis focuses on the IEW $$$R_2$$$. Voxels across the white matter were binned according to local fiber orientation in $$$5^\circ$$$ intervals. The IEW $$$R_2$$$ was plotted as a function of fibre orientation after averaging over all subjects. The diffusion-mediated orientation-dependent model $$$R_2(\theta)=R_{2,\text{iso}}+R_{2,\text{aniso}}\sin^4\theta$$$ was fit to the data for each TE. A $$$T_2$$$-water phantom was scanned at three different echo spacings ($$$\text{TE}=6,12,16$$$ms) with the same protocol and DECAES analyses as the in vivo data.To investigate the degree to which vasculature could be responsible for diffusivity-driven orientation dependence, we simulated a three dimensional voxel filled with cylindrical blood vessels6. Within this voxel, the Bloch-Torrey equation9 $$\frac{\partial}{\partial_t}m=\nabla\cdot{}\left(D\nabla{}m\right)-\left(R_2(x)+i\omega(x)\right)m$$ was solved, where $$$m=m_x+im_y$$$ is the complex transverse magnetization, $$$R_2(x)$$$ is the local relaxation rate, and $$$\omega(x)$$$ is the local magnetic field in units of $$$\text{rad}/\text{s}$$$. Simulations were performed for multiple TE and field angles $$$\theta$$$. For each simulation, the simulated voxel was divided into three regions: tissue, blood, and fluid-filled perivascular space (PVS). All interfaces were made impermeable by prescribing Neumann boundary conditions. An isotropic bed of cylindrical capillaries was simulated, $$$1/3$$$ of which were arteries and the rest veins. Three large blood vessels (one artery) were included which represent vessels running along WM fibre tracts. Myelinated WM fibres were not included due to the computationally infeasible sum-micrometer resolution which would be required. See Table 2 for a full list of simulation parameters, and Figure 4 for the simulation domain.
Results and Discussion
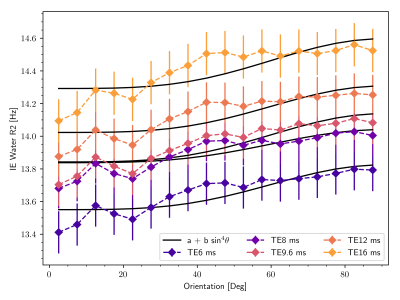
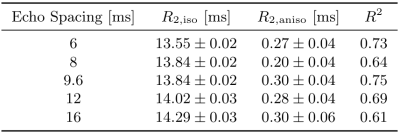
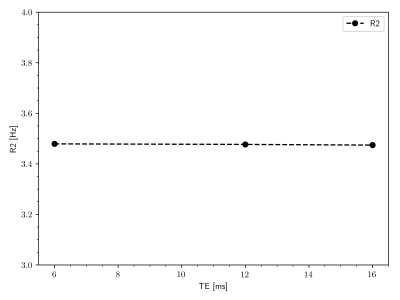
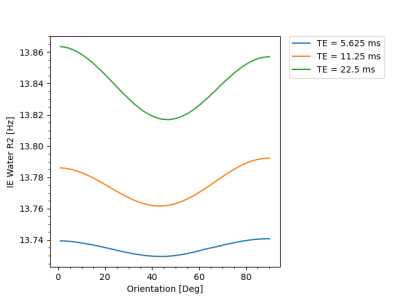
Figure 1 shows that IEW $$$R_2$$$ exhibits an orientation-independent increase with increasing TE. The $$$R_2(\theta)=R_{2,\text{iso}}+R_{2,\text{aniso}}\sin^4\theta$$$ model fits exhibit large deviations from the experimental data, particularly in the $$$30-50^\circ$$$ range. In Table 2, the resulting fit parameters are shown. The orientation-independent parameter $$$R_{2,\text{iso}}$$$ increases with increasing TE, however, the diffusion-sensitive parameter $$$R_{2,\text{aniso}}$$$ shows no significant change with varying TE, indicating that diffusion may not play a large role in the overall orientation-dependence. Figure 2 shows that the measured $$$R_2=3.48\text{Hz}$$$ of the $$$T_2$$$-water phantom does not vary with echo spacing, ruling out systemic scanner effects as an explanation for the $$$R_2$$$ variation with TE in vivo.Figure 3 shows IEW $$$R_2$$$ resulting from the Bloch-Torrey simulations. The observed orientation-dependence is less than 0.3% for all echo spacings, with $$$R_2(\theta)$$$ reaching a minimum near $$$45-50^\circ$$$ and maxima at $$$0^\circ,90^\circ$$$; the observed curves match neither the magnitude nor direction of the orientation-dependence of in vivo data.
In this work we have shown that IEW $$$R_2$$$ depends on echo spacing as well as orientation when measured using multi spin-echo, and that diffusion-mediated decoherence due to field inhomogeneities formed by blood vessels is not able to explain the observed dependencies. However, our simulations ignore the anisotropy of white matter due to numerical limitations. Therefore, diffusion at the length scale of the myelinated white matter cannot be excluded as a possible explanation.
Acknowledgements
Natural Sciences and Engineering Research Council of Canada, Grant/Award Number 016-05371; the Canadian Institutes of Health Research, Grant Number RN382474-418628; the National MS Society (RG-1507-05301). J.D. is supported by NSERC Doctoral Award and Izaak Walton Killam Memorial Pre-Doctoral Fellowship; A.R. is supported by Canada Research Chairs 950-230363. UBC Vancouver is located on the traditional, ancestral, and unceded territory of the Musqueam people.References
1. M. J. Knight, B. Wood, E. Couthard, and R. Kauppinen, “Anisotropy of spin-echo T2 relaxation by magnetic resonance imaging in the human brain in vivo,” Biomed. Spectrosc. Imaging, vol. 4, no. 3, pp. 299–310, Jan. 2015, doi: 10.3233/BSI-150114.
2. M. J. Knight, S. Dillon, L. Jarutyte, and R. A. Kauppinen, “Magnetic Resonance Relaxation Anisotropy: Physical Principles and Uses in Microstructure Imaging,” Biophys. J., vol. 112, no. 7, pp. 1517–1528, Apr. 2017, doi: 10.1016/j.bpj.2017.02.026.
3. C. Birkl, J. Doucette, M. Fan, E. Hernández‐Torres, and A. Rauscher, “Myelin water imaging depends on white matter fiber orientation in the human brain,” Magn. Reson. Med., vol. 85, no. 4, pp. 2221–2231, 2021, doi: https://doi.org/10.1002/mrm.28543.
4. S.-H. Oh, Y.-B. Kim, Z.-H. Cho, and J. Lee, “Origin of B0 orientation dependent R2* (=1/T2*) in white matter,” NeuroImage, vol. 73, pp. 71–79, Jun. 2013, doi: 10.1016/j.neuroimage.2013.01.051.
5. C. M. W. Tax, E. Kleban, M. Chamberland, M. Baraković, U. Rudrapatna, and D. K. Jones, “Measuring compartmental T2-orientational dependence in human brain white matter using a tiltable RF coil and diffusion-T2 correlation MRI,” NeuroImage, vol. 236, p. 117967, Aug. 2021, doi: 10.1016/j.neuroimage.2021.117967.
6. J. Doucette et al., “Rapid solution of the Bloch-Torrey equation in anisotropic tissue: Application to dynamic susceptibility contrast MRI of cerebral white matter,” NeuroImage, vol. 185, pp. 198–207, Jan. 2019, doi: 10.1016/j.neuroimage.2018.10.035.
7. M. J. Knight and R. A. Kauppinen, “Diffusion-mediated nuclear spin phase decoherence in cylindrically porous materials,” J. Magn. Reson., vol. 269, pp. 1–12, Aug. 2016, doi: 10.1016/j.jmr.2016.05.007.
8. J. Doucette, C. Kames, and A. Rauscher, “DECAES - DEcomposition and Component Analysis of Exponential Signals,” Z. Med. Phys., May 2020, doi: 10.1016/j.zemedi.2020.04.001.
9. H. C. Torrey, “Bloch Equations with Diffusion Terms,” Phys. Rev., vol. 104, no. 3, pp. 563–565, Nov. 1956, doi: 10.1103/PhysRev.104.563.
10. M. Holz, S. R. Heil, and A. Sacco, “Temperature-dependent self-diffusion coefficients of water and six selected molecular liquids for calibration in accurate 1H NMR PFG measurements,” Phys. Chem. Chem. Phys., vol. 2, no. 20, pp. 4740–4742, Jan. 2000, doi: 10.1039/B005319H.
11. J. M. Zhao, C. S. Clingman, M. J. Närväinen, R. A. Kauppinen, and P. C. M. van Zijl, “Oxygenation and hematocrit dependence of transverse relaxation rates of blood at 3T,” Magn. Reson. Med., vol. 58, no. 3, pp. 592–597, Sep. 2007, doi: 10.1002/mrm.21342.
12. J. Spijkerman, E. Petersen, J. Hendrikse, P. Luijten, and J. Zwanenburg, “T 2 mapping of cerebrospinal fluid: 3 T versus 7 T,” Magn. Reson. Mater. Phys. Biol. Med., Nov. 2017, doi: 10.1007/s10334-017-0659-3.
13. A. Deistung, A. Rauscher, J. Sedlacik, J. Stadler, S. Witoszynskyj, and J. R. Reichenbach, “Susceptibility weighted imaging at ultra high magnetic field strengths: Theoretical considerations and experimental results,” Magn. Reson. Med., vol. 60, no. 5, pp. 1155–1168, Nov. 2008, doi: 10.1002/mrm.21754.
14. E. Hernández-Torres et al., “Anisotropic cerebral vascular architecture causes orientation dependency in cerebral blood flow and volume measured with dynamic susceptibility contrast magnetic resonance imaging,” J. Cereb. Blood Flow Metab., vol. 37, no. 3, pp. 1108–1119, Mar. 2017, doi: 10.1177/0271678X16653134.
15. R. M. Weisskoff and S. Kiihne, “MRI susceptometry: Image-based measurement of absolute susceptibility of MR contrast agents and human blood,” Magn. Reson. Med., vol. 24, no. 2, pp. 375–383, Apr. 1992, doi: 10.1002/mrm.1910240219.
Figures