Introduction

The gradient modulation transfer function (GMTF) contains crucial information about the MRI gradient system. Assuming a linear, time-invariant model (LTI), the MRI gradient system’s response for any given input gradient waveform with limited energy can be calculated. This enables to correct for inevitable system imperfections and to subsequently improve reconstructed image quality. Common methods use concurrent field monitoring¹ or acquisition of the GMTF², which allows correcting for MRI gradient system shortcomings in post-processing. However, these methods are either expensive, time-intensive, or not fully universal (e.g. temperature dependence of the GMTF³). In this work, we present an automatic identification of mechanical resonances by using mobile phone audio recordings exclusively. The use case is demonstrated for PC-MRI, by suggesting combinations of echo (TE) and repetition time (TR) to minimize undesirable residual background phase. For EPI sequences, optimal EPI readout bandwidths (EPI BW) are derived such that beat phenomena are minimized.

Methods

Building upon knowledge from previous works concerned with the identification of the acoustic transfer function from chirp sequences⁴ and the minimization of background phase in PC-MRI sequences⁵, a web-based framework is proposed to automatically identify mechanical resonances of the MRI gradient system.

The webapp is built based on a template (https://github.com/ialja/beautiful-web) in flask (https://github.com/pallets/flask), employing a python backend which is easily extendable for custom analysis code and deployable on a cloud application platform (https://www.heroku.com). The input data mask offers the possibility to either use example data, record data online or upload an audio file for usage in the workflow. The example data comprises a tailored MR sequence which covers the audio spectrum in the frequency region of interest (0Hz to 2kHz) on all axes (Figure 1). If needed, a single axis can be selected for distinguishing between mechanical resonances on different axes. Other input data, such as fMRI sequences employing a long TR, are equally suitable.

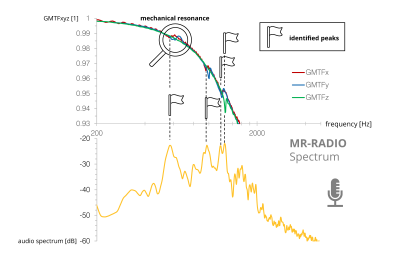
The input audio file is processed using its autocorrelation function and its Fourier transform (MR-RADIO spectrum), where the former is used to estimate the TR and the latter to identify mechanical resonances by marking peaks in the audio spectrum.

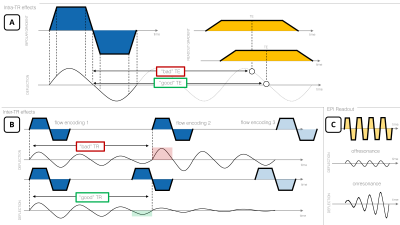
Following theoretical considerations presented in ⁵, for PC-MRI sequences, the suggested TE is found when the deflection due to the bipolar velocity encoding gradient has its zero crossing at TE (Figure 2A).

Optimal TRs, on the other hand, are derived if subsequent bipolar gradients are opposite in phase relative to the deflection (Figure 2B). For sequences besides PC-MRI, TR can be optimized such that the gradient spectrum (Fourier transform of the gradient waveforms) has zero-crossings at the mechanical resonance frequencies. This is possible due to the inherent comb-like gradient spectrum of repetitive MR sequences.

For EPI readouts, as the amplitude of the beat phenomenon scales with $$$1 / (f_{EPI}^2 - f_{res}^2)$$$⁶, it is desirable to maximize the distance $$$f_{EPI}$$$ and $$$f_{res}$$$ for the readout train on a given axis, given a non-oblique image orientation. As the input audio file may comprise gradient waveforms played out on all axes (oblique slice), the distance to the identified mechanical resonances is maximized.

Results & Discussion

Figure 1 compares the GMTF with the MR-RADIO spectrum, confirming the feasibility of identifying mechanical resonances in the spectrum. As seen, the mechanical resonances on all gradient axes, as identified using the MR-RADIO approach, agree well with the mechanical resonances in the GMTF.

Figure 2 highlights the theoretical considerations regarding (A) the suggestion of beneficial TE, (B) TR timings and (C) EPI readout bandwidths. Given a typical mechanical resonance frequency of $$$f_{res} = 1\mathrm{kHz}$$$, a shift of TE of max. $$$\lambda / 4 = 1 / (4 f_{res}) = 0.25\mathrm{ms}$$$ results in minimizing the background phase. Beneficial TRs are given by $$$(2n-1) / (2 f_{res})$$$. If the optimal TR cannot be achieved or for sequences besides PC-MRI, TR can be set to irrational multiples of $$$1 / f_{res}$$$.

Figure 3 presents a screen recording of the MR-RADIO workflow exemplifying its ease of use and its reporting functions.

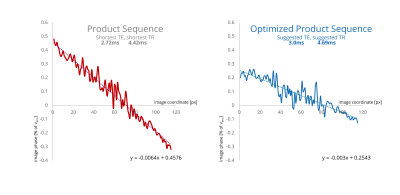
Figure 4 compares the background phase resulting from standard sequence parameters for a vendor supplied PC-MRI sequence (shortest TE/TR). The background phase slope is found to be reduced by 50%.

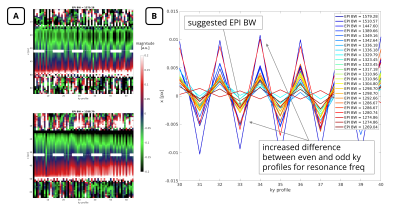
Figure 5 shows EPI data recorded with deactivated phase encoding blips and Fourier transform in phase encoding direction for nominal (highest EPI BW) and MR-RADIO suggested EPI BW parameters in a stationary, spherical phantom. Employing the suggested values, a reduced discrepancy between even and odd k_y lines is seen.

Conclusion

In this work, MR-RADIO, a web-based framework, has been presented, which offers easy, low-cost and ubiquitous identification of mechanical resonances of MRI gradient systems. The identified resonance frequencies help to guide optimal TE and TR setting in e.g. PC-MRI or to choose optimal readout bandwidths for EPI sequences, minimizing beat phenomena and N/2 ghost intensity.

Acknowledgements

The authors acknowledge funding of the Platform for Advanced Scientific Computing of the Council of Federal Institutes of Technology (ETH Board), Switzerland.