Introduction

Since its introduction in the seminal work from Lustig et al.¹, compressed sensing and iterative MR reconstruction enabled unprecedented acceleration in MR imaging without harming image quality, significantly improving patient comfort. In the last few years, the widespread diffusion of open-source image reconstruction frameworks, such as BART², Gadgetron³ and SigPy⁴, allowed researchers to further develop novel advanced reconstruction strategies. Among these, model-based reconstruction⁵ represents a promising research area, enabling fast and artefact-free parametric mapping of the tissues by incorporating knowledge of the physics in the encoding model. This approach has a significant computational burden, which can be alleviated by approximating MR signal with a linear combination of a basis function representing the space of possible signal evolutions, i.e. constraining the solution on a low-rank subspace^5,6. Many iterative and model-based reconstruction requires the use of Non-Cartesian k-space sampling trajectories. While several efficient open-source implementations of Non-Uniform Fourier Transform (NUFFT) exist, to the best of our knowledge there are no implementation specifically optimized for low-rank model-based reconstructions. Here, we introduce a fast and memory-efficient open-source NUFFT implementation embedding the low-rank projection operation. The library will be made publicly available under https://github.com/FiRMLAB-Pisa/lr-nufft-torch to interested researchers.

Methods

Theory
Non-Uniform Fourier transform with embedded low-rank projection and its adjoint can be represented by the following equations⁷:
$$ y = (\phi G)\cdot F \cdot P \cdot A \cdot x (NUFFT) $$
$$ x = A \cdot P^H \cdot F^H \cdot (G^H \phi^H) D y (NUFFT adjoint) $$
Where A, P, F, G, $$$\phi$$$ represent apodization, signal padding, Cartesian Fourier Transform, interpolation to non-Cartesian location and projection from low-rank basis to time domain; here, H represents adjoint operation and D is the density compensation function. Cartesian to Non-Cartesian interpolation and its adjoint (gridding) represents the most intensive computational steps; here, they are fused with the subspace projection operator to allow for compiler optimization and reduce memory usage. Pseudo-code for fused operation is shown in Figure 1.

Implementation details
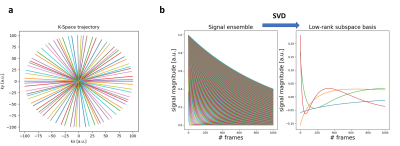
The library is written in Python 3.7. Core operators (padding, apodization, Cartesian Fourier transform) are based on Pytorch 1.10, while fused projection-interpolation/-gridding are written in Numba 0.54.1 (an open-source Just-In-Time compiler for Python) to allow fast computation and easy deployment. Fused projection-interpolation/-gridding exploit Numba parallelization to speed-up computation. Parallelization is performed over frames and image batches (i.e. different receive channels and slices) to avoid writing conflicts. Interpolation was adapted from the Kaiser-Bessel convolution gridding included in SigPy⁴. To achieve short computation time while maintaining Validation and Benchmark To test our library, we simulated a Fast-Spin Echo acquisition for T2 mapping. A Shepp-Logan phantom was used as a virtual object. The phantom was segmented in three regions corresponding to White Matter (T2=70ms), Gray Matter(T2=83ms) and CSF (T2=329ms). K-space sampling was based on a 2D radial projection with golden-angle ordering of the spokes (Figure 2a). Low-rank subspace basis was computed by simulating an ensemble of 300 spin (T2=1:329ms, linearly spaced) with the following signal equation: where the echo time TE ranged from 1 to 300ms Figure 2b. In this experiment, we simulated a k-t acquisition with 1000 echo times (here called frames), each sampled with 100 spokes of the trajectory. Ground truth subspace coefficient for the virtual object were generated by projecting signal evolution corresponding to phantom tissues on the subspace basis. We assessed the performances of the library by comparing it with a recent open-source implementation (Torch-KB-NUFFT8). Zero-filled k-space data for all the subspace coefficients were pre-computed to be fed into Torch-KB-NUFFT routines, in order to fully exploit its capability. All the tests were performed on a laptop equipped with an Intel Xeon 12 Core CPU and 32GB of RAM.

Results and Discussion

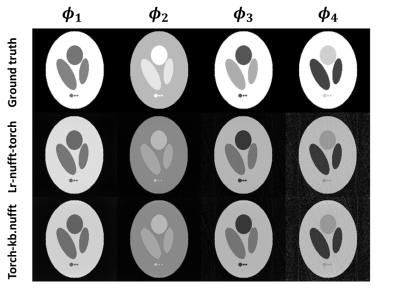
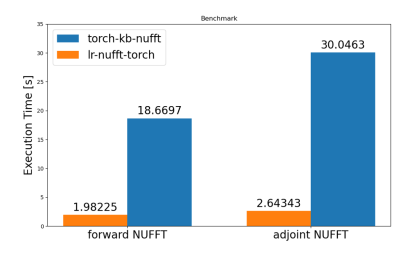
Figure 3 shows the comparison between ground truth, Torch-KB-NUFFT NUFFT-adjoint results and our implementation. Both our implementation and Torch-KB-NUFFT achieve comparable results. Figure 4 shows the difference in terms of computation times. Our implementation outperforms Torch-KB-NUFFT by an order of magnitude both for forward and adjoint steps. Here, we demonstrated significant speed-up of NUFFT for low-rank constrained reconstruction compared to available open-source implementation. While the Echo train length (1000 echoes) is much longer than realistic implementations, modern approaches such as MR Fingerprinting9 easily reach these values. Similarly to Torch-KB-NUFFT, our NUFFT operators are wrapped as Pytorch Module operators and could be used in end-to-end Deep Learning reconstructions. Being based on pure Python, with acceleration via Numba, the proposed implementation is easy to extend. Further performance gain could be achieved at cost of readability by using lower level languages such as C++ in fused interpolation/subspace projection. Future work will be focused on test the library on massively parallel computational devices (such as GPUs). However, this should be relatively straightforward thanks to Numba and Pytorch backends. In addition, we will test the library in higher dimensional problems (3D+t) and fused self-adjoint operators to speed-up iterative algorithms.

Conclusion

The proposed implementation reaches one order of magnitude of speed-up in fused NUFFT and low rank projection while maintaining comparable image quality.

Acknowledgements

The results here presented have been developed in the framework of the 18HLT05 QUIERO Project. This project has received funding from the EMPIR Programme co-financed by the Participating States and from the European Union’s Horizon 2020 Research and Innovation Programme.