Introduction

Inhomogeneities of the static magnetic field and radiofrequency transmit is unavoidable in MRI, causing distortions in the intensity of the acquired MR images. To increase the quality of the obtained intensities, accurate determination of the spatial distribution of those fields is required. Chemical Exchange Saturation Transfer (CEST) imaging¹, a molecular MRI technique nowadays available also on clinical 3T MRI scanners, is also affected by inhomogeneities of the static magnetic (B₀) and radiofrequency (RF) transmit (B₁) fields.
Some sequences have been proposed for separate B₀^2,3 and B₁⁴ mapping, but in⁵,a unique sequence is described for mapping both inhomogeneity maps, called “Simultaneous mapping of Water Shift And B1 (WASAB1)” (Figure1A,Figure1B).
Sampling of several frequency offsets $$$\Delta(\omega)$$$ around the water resonance frequency, a WASAB1-Spectrum is acquired and normalized using a M₀ image whose frequency is far from the water one. The WASAB1 normalized intensities Z(Δω) of a single voxel can be modelled based on the Bloch equations as^5,6 :
$$ Z(\Delta\omega)=|c-d\cdot f(B_0,B_1,\Delta(\omega))| \;\;\;\;\;\;\;\;\;\; (1)$$
with
$$f(B_0,B_1,\Delta(\omega))=\sin^2\left(\tan^{-1}\left(\frac{\bar\gamma \cdot B_1}{freq\cdot(\Delta\omega-B_0)}\right)\right) \cdot sin^2\left(\left(\left ( \frac{\bar\gamma \cdot B_1}{freq}\right)+(\Delta\omega-B_0)^2\right)^{\frac{1}{2}} \cdot\frac{t_p}{2}\right) \;\;\;\;\;\;\;\;\;\;(2)$$
where parameters c and d describe WASAB1-Spectra amplitude, B₁ its periodicity, B₀ its symmetry axis ($$$freq=123MHz$$$ at 3T, $$$\bar\gamma=42.578MHz/T,t_p=5.12ms$$$) (see Figure1A).

B₀ and B₁ are estimated by fitting this model for every voxel of the WASAB1 images. However, the parameter estimation is difficult and unstable due to the presence of the absolute value in Equation1, that models the acquired MRI-magnitude and introduces discontinuity in the model.
The classical WASAB1 postprocessing method proposed in⁵ consists of two steps: i) exhaustive search on a coarse parameter grid; ii) refinement of the solution with a nonlinear optimization algorithm. However, it significantly increases the computational time of the model fitting, that is prohibitive in clinical use.

Methods

Technical Solution:
Our proposed method is divided in two steps. For each voxel: i) retrieve the sign of some data points of the WASAB1-Spectra to generate a polarized dataset, ii) knowing the sign of the signal, the absolute value in Equation1 can be removed and the model becomes linear in parameters c and d. Hence, the variable projection method⁷ can be applied to reduce the dimensionality of the nonlinear estimation problem. This makes the estimate of B₀ and B₁ faster by two orders of magnitude, more robust, and less sensitive to local minima.
The polarized dataset is constructed by removing the data points that are unlikely to be positive (Figure1C). It is an iterative process that starts at the extremities of the WASAB1-Z-spectra. Moving toward the central frequency offsets of the spectrum, it extrapolates the WASAB1-Z-spectra at the next frequency offset and checks if the predicted value is likely to be positive or negative. The extrapolated value at the i^th offset is constructed as $$$Z_i=Z_{i-1}-\delta$$$, where $$$\delta$$$ is the maximum signal variation between two offsets in the current spectra. This yields a partial polarized WASAB1-Z-spectrum, from which first guess of B₀ and B₁ can be estimated. Those approximations are then used to refine the sign of the signal on the whole spectra, which is eventually used to derive the definitive estimate of B₀ and B₁ (Figure1D).

Data Simulation:
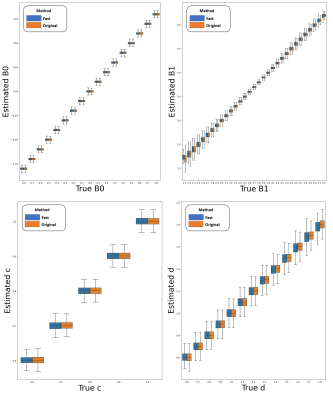
To evaluate the robustness of the proposed method, WASAB1-Z-Spectra were generated applying Equation1 for the following parameter space: $$$c=[0.6:0.1:1]$$$, $$$d=[0.6:0.1:1.8]$$$, $$$B_1=[2.2:0.1:5.2]$$$ and $$$B_0=[-0.8:0.1:0.8]$$$. Rician noise was added to the generated WASAB1-Z-Spectra with $$$SNR=30$$$. Finally, the parameter estimation was performed for each voxel of the generated phantom data, using the original⁵ and the proposed method.

Patient Data Acquisition:
The WASAB1 data were acquired on a 3 Tesla MRI scanner (Prisma, Siemens Healthineers, Germany) equipped with a 64-channel head and neck coil, on 10 persons with relapsing-remitting multiple sclerosis (pw-RRMS), in the framework of a clinical CEST study (Figure2). The WASAB1 sequence (WIP816B) used a 3D snapshot-GRE with the following parameters: FOV=220×180mm²; matrix=128×104; voxel size=1.7×1.7×5mm³; slices=12; TE=2.00ms; TR=4.5ms; bandwidth=700 Hz/pixel; flip angle=6°; 23 WASAB1-volumes acquired at $$$\Delta\omega_i=-1.8ppm:0.16ppm:1.8ppm+M_0$$$ with 1 rectangular preparation pulse t_p/t_delay=5.12/100ms; acquisition time=123sec.

Processing:
The acquired WASAB1 sequences were motion-corrected using SimpleElastix⁸, skull-stripped, normalized by M0, then processed by self-written Python code for the classic^5,6 and our proposed method.

Results

Both the evaluation on the generated phantom data (Figure3) and on the in vivo 3 Tesla data (Figure4) showed that our proposed method is in good agreement with the original WASAB1 method⁵, with Figure4 showing differences between the estimated values of maps of each method below 0.02 for the majority of pairs in the Bland-Altman plots.
Figure5 shows a clinical Amide Proton Transfer weighted (APTw)¹ CEST map, B₀-B₁ corrected⁹ with the inhomogeneity maps processed with our method, of one person with pw-RRMS.

Discussion

Our method led to an average computation time of 0.0007 seconds for a single WASAB1-Z-Spectrum compared to 18.3 seconds for the reference method. Using parallel execution on the same 8-core processor an entire WASAB1 clinical multi-volume was processed in less than 5 seconds in Olea Sphere 3.0 (Olea Medical, La Ciotat, France).

Conclusion

A new accelerated post-processing method has been proposed for simultaneous B₀ and B₁ mapping based on the WASAB1 sequence. Its outstanding acceleration permits its use in clinical routine for CEST inhomogeneity correction, without compromising the stability of the estimated B₀ and B₁ maps.

Acknowledgements

The clinical study was kindly supported by MS Research Australia. I.Khormi was supported by a PhD scholarship with annual grant support from the University of Jeddah, Saudi Arabia.