2708

Quantitative magnetization transfer: Estimation of the Semi-Solid Spin Pool's T1

Sebastian Flassbeck^1,2 and Jakob Assländer^1,2
¹Center for Biomedical Imaging, New York University School of Medicine, New York, NY, United States, ²Center for Advanced Imaging Innovation and Research, New York University School of Medicine, New York, NY, United States

Synopsis

Most magnetization transfer experiments are insensitive to the longitudinal relaxation rate of the invisible semi-solid spin pool and it has become common practice to heuristically assume 1/second. This assumption has, however, been challenged recently. Because this parameter is notoriously hard to estimate, previous studies have relied on the analysis of large white matter regions or the entire brain. Here, we explore the ability to estimate this value on a voxel-by-voxel basis with an MR-Fingerprinting-like pulse sequence.

Introduction

Commonly, magnetization transfer¹ (MT) is described by a 2-pool model² that distinguishes between protons bound in water—the so-called free pool—and protons bound in macromolecules—the so-called semi-solid pool. The original MT experiments drive the coupled spin system into a steady state with continuous radio frequency waves.² Such scans are rather insensitive to the longitudinal relaxation rate of the semi-solid spin pool $$$R_1^s$$$ and it has become common practice to heuristically assume $$$R_1^s=1$$$/s² or to assume equal relaxation rates in the free and semi-solid spin pools ($$$R_1^s=R_1^f$$$),³ which are very similar assumptions given that $$$R_1^f\approx1$$$/s in white matter. These assumptions are, however, increasingly questioned^4,5,6 and values in the range $$$2/\text{s}\lesssim R_1^s\lesssim 6.5/\text{s}$$$ have been estimated instead. As $$$R_1^s$$$ is notoriously hard to estimate, these measurements do, however, all rely on fits to signal-averages over large regions of interest^4,5 or the entire brain.⁶ In the light of the recent advances in fast quantitative MRI that were driven by MR Fingerprinting,⁷ we here explore the possibility to estimate $$$R_1^s$$$ on a voxel-by-voxel basis, along with other MT parameters.

Methods

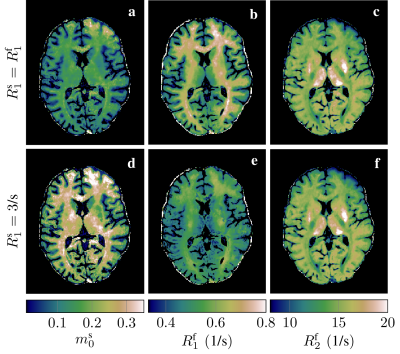
After getting informed consent, we scanned an asymptomatic volunteer at 3T. We used a hybrid-state free precession⁸ pulse sequence that was optimized for quantitative MT.⁹ It inverts the free spin pool with a rectangular $$$\pi$$$-pulse¹⁰ and, thereafter, subscribes a train of RF-pulses with varying flip angles and pulse durations to drive the magnetization onto an optimized trajectory. We acquired highly undersampled k-space data with a 3D-radial koosh-ball trajectory with a 2D golden-means increment,^11,12 reconstructed images directly in a low-rank space^13,14 and fitted a two-pool model to this data, where the semi-solid spin pool is described by the generalized Bloch equations.¹⁵

In a first scan, we use a pulse train that was optimized for quantifying the fractional size of the semi-solid pool $$$m_0^s$$$, $$$R_1^\text{apparent}=R_1^f=R_1^s$$$, and $$$R_2^f$$$, while accounting for the full model with the additional parameters $$$R_\text{exchange},T_2^s$$$, and a complex-valued scaling factor. This data was acquired with 1mm isotropic resolution in 12 minutes and allows us to compare two fits: one with the constraint $$$R_1^s=R_1^f$$$, and one with the constraint $$$R_1^s=3$$$/s. Both fits assume $$$T_2^s=10\mu$$$s and a perfectly calibrated $$$B_1$$$, and fit the parameters $$$m_0^s,R_1^f,R_2^f,R_\text{exchange},B_0$$$, and a complex valued scaling factor.

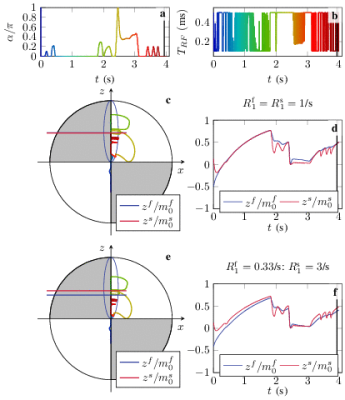
We optimized a second pulse train to estimate $$$m_0^s,R_1^f$$$, and $$$R_2^f$$$, while considering $$$R_1^s$$$ an additional, independent fit parameter. The resulting spin dynamics is sketched in Fig. 1 for both assumptions: for $$$R_1^s=R_1^f$$$, we observe $$$z^s/m_0^s\approx z^f/m_0^f$$$ for most of the trajectory (c,d), and with the assumption $$$R_1^s\gg R_1^f$$$, we observe $$$z^s/m_0^s>z^f/m_0^f$$$ for most of the trajectory, which indicates that the semi solid pool is a major driving factor of apparent longitudinal relaxation of the free pool in this case (e,f).

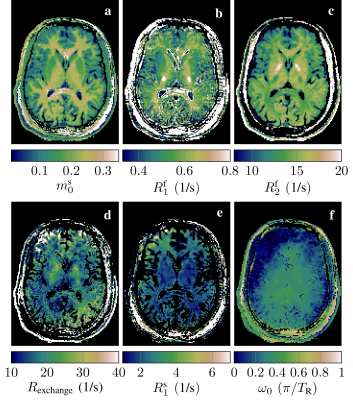
We scanned a second asymptomatic volunteer with this pulse sequence with an isotropic resolution of 1.6mm and fitted the parameters $$$m_0^s,R_1^f,R_1^s,R_2^f,R_\text{exchange},B_0$$$, and a complex-valued scaling factor, while assuming $$$T_2^s=10\mu$$$s and a perfectly calibrated $$$B_1$$$. Note that the lower resolution was chosen for practical reasons only.

Results

The first scan allows for a direct comparison of fits with the traditional constraint $$$R_1^s=R_1^f$$$ and with the constraint $$$R_1^s=3$$$/s, which is in the range of recent estimates^4,5,6 (Fig. 2). Assuming $$$R_1^s=R_1^f$$$, we observe white matter values that are in line with literature.^16,10,3 The assumption of fast $$$R_1^s$$$ results in a substantially larger size of the semi-solid pool (d vs. a), which has been also observed by van Gelderen et al.⁵ (Tab. 1). Further, we observe a slower $$$R_1^f$$$, which is also in line with previous findings,^4,5,6 while $$$R_2^f$$$ remains largely unaffected.

With a tailored pulse sequence, we tested the feasibility of fitting a full model with varying $$$R_1^s$$$ (Fig. 3) and we observe white matter values of $$$R_1^s=2.4$$$/s and an $$$m_0^s=24\%$$$, confirming the findings of Gelderen et al. with this voxel-by-voxel fit. Further, we observe very little WM/GM contrast in $$$R_1^f$$$, which is in line with the findings of Samsonov and Field.⁶ Note that this pulse sequence was optimized to estimate $$$m_0^s,R_1^f$$$, and $$$R_2^f$$$ (first row in Fig. 3) while accounting for the full model, i.e. we do not expect good estimates in remaining parameters (second row). Further, we note that the assumption $$$R_1^s=R_1^f$$$ results in values that diverge from the first scan, further indicating that this model is incomplete.

Discussion and Conclusions

We demonstrated the feasibility of fitting a full qMT model, including a fast $$$R_1^s$$$, on a voxel-by-voxel basis. Key to this sensitivity is a tailored hybrid-state pulse sequence⁸ that evokes information-rich spin dynamics. Future work will include an exploration of the accuracy with which we estimate each of the model parameters (including $$$R_1^s$$$) when optimizing the pulse sequence for this task. Further, we will translate this approach to a protocol with 1mm isotropic resolution, similar to the protocol used for Fig. 2.

Acknowledgements

This work was supported by grant NIH/NIBIB R21 EB027241 and was performed under the rubric of the Center for Advanced Imaging Innovation and Research, a NIBIB Biomedical Technology Resource Center (NIH~P41 EB017183).

References

1. Steven D. Wolff and Robert S. Balaban. Magnetization transfer contrast (MTC) and tissue water proton relaxation in vivo. Magn.Reson. Med., 10(1):135–144, 1989

2. RM M Henkelman, X Huang, Q-S S Xiang, Greg J Stanisz, SD D Swanson, and MJ J Bronskill. Quantitative Interpretation of Magnetization Transfer. Magn. Reson. Med., 29(6):759–766, 1993

3. Richard D. Dortch, Ke Li, Daniel F. Gochberg, E. Brian Welch, Adrienne N. Dula, Ashish A. Tamhane, John C. Gore, and Seth A. Smith.Quantitative magnetization transfer imaging in human brain at 3 T via selective inversion recovery. Magn. Reson. Med., 66(5):1346–1352,2011.

4. Gunther Helms and Gisela E. Hagberg. In vivo quantification of the bound pool T1 in human white matter using the binary spin–bath model of progressive magnetization transfer saturation. Phys. Med. Biol., 54(23):N529–N540, dec 2009.

5. Peter van Gelderen, Xu Jiang, and Jeff H. Duyn. Effects of magnetization transfer on T1 contrast in human brain white matter.Neuroimage, 128:85–95, mar 2016.

6. Alexey Samsonov and Aaron S. Field. Confounding of Macromolecular and Paramagnetic Tissue Content in Quantitative MTI Remediedby Explicit Estimation of Bound Pool Relaxation. In Proc. Intl. Soc. Mag. Reson. Med. 29, page 0716, 2021.

7. Dan Ma, Vikas Gulani, Nicole Seiberlich, Kecheng Liu, Jeffrey L. Sunshine, Jeffrey L. Duerk, and Mark A. Griswold. Magnetic resonance fingerprinting. Nature, 495(7440):187–192, 2013.

8. Jakob Assländer, Dmitry S Novikov, Riccardo Lattanzi, Daniel K Sodickson, and Martijn A Cloos. Hybrid-state free precession in nuclear magnetic resonance. Nat. Commun. Phys., 2(1):73, dec 2019.

9. Jakob Assländer and Daniel K Sodickson. Quantitative Magnetization Transfer Imaging in the Hybrid State. In Proc. Intl. Soc. Mag. Reson. Med. 27, page 1104, 2019.

10. Daniel F. Gochberg and John C. Gore. Quantitative imaging of magnetization transfer using an inversion recovery sequence. Magn. Reson. Med., 49(3):501–505, 2003

11. Rachel W. Chan, Elizabeth A. Ramsay, Charles H. Cunningham, and Donald B. Plewes. Temporal stability of adaptive 3D radial MRI using multidimensional golden means. Magn. Reson. Med., 61(2):354–363, feb 2009.

12. Sebastian Flassbeck and Jakob Assländer. Minimization of Eddy Current Related Artefacts in HSFP Sequences. In Proc. Intl. Soc. Mag. Reson. Med. 29, page 1560, 2021.

13. Jonathan I. Tamir, Martin Uecker, Weitian Chen, Peng Lai, Marcus T. Alley, Shreyas S. Vasanawala, and Michael Lustig. T2 shuffling: Sharp, multicontrast, volumetric fast spin-echo imaging. Magn. Reson. Med., 77(1):180–195, 2017

14. Jakob Assländer, Martijn A Cloos, Florian Knoll, Daniel K Sodickson, Jürgen Hennig, and Riccardo Lattanzi. Low rank alternating direction method of multipliers reconstruction for MR fingerprinting. Magn. Reson. Med., 79(1):83–96, jan 2018.

15. Jakob Assländer, Cem Gultekin, Sebastian Flassbeck, Steffen J Glaser, and Daniel K Sodickson. Generalized Bloch model: a theory forpulsed magnetization transfer. Magn Reson Med, page doi: 10.1002/mrm.29071, jul 2021.

16. Greg J Stanisz, Ewa E Odrobina, Joseph Pun, Michael Escaravage, Simon J Graham, Michael J Bronskill, and R Mark Henkelman. T1, T2 relaxation and magnetization transfer in tissue at 3T. Magn Reson Med, 54(3):507–512, 2005.

Figures

Fig. 1: a Flip angles and b pulse durations of an optimized hybrid-state pulse sequence. The objective of the optimization was an optimal encoding of m₀^s, R₁^f, and R₂^f, while fitting a full qMT model, including a fast R₁^s component (cf. Fig. 3); c,d depicts the evoked spin dynamics with the more common assumption R₁^s = R₁^f, and e,f with the here explored assumption R₁^s >> R₁^f. In the latter case, we observe z^s/m₀^s > z^f/m₀^f for most of the spin trajectory, which indicates that the semi-solid spin pool plays a major role in the apparent T₁ relaxation of the free pool.

Fig. 2: Comparison of fits with two different models to the same data. The top row depicts fits that assume R₁^s = R₁^f, which is in line with the assumptions commonly made in qMT, and the estimated parameters are in line with the ones commonly reported. The fits shown in the bottom row assume R₁^s = 3/s >> R₁^f, which results in a substantially higher m₀^s and lower R₁^f, in line with the values reported in Refs.^4,5,6 that perform similar analyses.

Fig. 3: Fit of the full qMT model. The utilized pulse sequence was optimized for estimating m₀^s, R₁^f, and R₂^f (top row), but the fit also estimates R_x, R₁^s, and the off-resonance frequency ω₀, while assuming T₂^s = 10μs and a perfectly calibrated B₁ field. We observe higher than usual m₀^s estimates, which is in line with the findings of Gelderen et al.⁵, and we find little GM/WM contrast in R₁^f, which was also observed by Samsonov⁶. R₁^s is estimated as 2.4/s in an ROI, which is also in line with previous estimates^4,5 (cf. Tab. 1).

Tab. 1: ROI analysis in the frontal white matter with all discussed model variations, where the gray cells indicate values that were fixed in the fit. When setting R₁^s = R₁^f in the fit (1^st column), the estimated parameters are in line with the most common literature values (4^th column). When assuming R₁^s = 3/s (2^nd column), or when fitting R₁^s(3^rd column), the estimated values are in line with the observations in Refs.^4,5,6 that propose that R₁^s is much faster than R₁^f(5^th column).

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

2708

DOI: https://doi.org/10.58530/2022/2708