2707

Generalized Bloch model: a theory for pulsed magnetization transfer
Jakob Assländer1,2, Cem Gultekin3, Sebastian Flassbeck1,2, Steffen J Glaser4, and Daniel K Sodickson1,2
1Center for Biomedical Imaging, New York University School of Medicine, New York, NY, United States, 2Center for Advanced Imaging Innovation and Research, New York University School of Medicine, New York, NY, United States, 3Courant Institute of Mathematical Sciences, New York University, New York, NY, United States, 4Department of Chemistry, Technische Universität München, München, Germany

Synopsis

We introduce a classical model to describe magnetization transfer (MT). Like a quantum-mechanical description of spin dynamics and like the original Bloch equations, but unlike existing MT models, the proposed model is based on the algebra of angular momentum in the sense that it explicitly models the rotations induced by radio-frequency (RF) pulses. It unifies the original Bloch model, Henkelman's steady-state theory for magnetization transfer, and the commonly assumed rotation induced by hard, i.e. short, pulses, and describes experimental data better than previous models.

Introduction

Commonly, magnetization transfer1 is described by a 2-pool model2 that distinguishes between protons bound in water—the so-called free pool—and protons bound in macromolecules—the so-called semi-solid pool. The original Henkelman model2 describes the steady-state MT effect during a continuous RF-wave. Existing models for RF-pulses3,4 build on Henkelman's model and show good agreement with experimental observations for off-resonant, several millisecond-long saturation pulses. For short RF-pulses, however, these models fail to describe the spin dynamics accurately. This becomes apparent when approaching the extreme case of a hard, i.e. instantaneous, pulse. Manning et al.5 demonstrated experimentally that a short inversion pulse does invert the semi-solid pool, which stands in contrast to existing MT models that predict a saturation of the semi-solid pool. Here, we propose a model that overcomes these limitations and describes first experimental data well.

Theory

Assuming, for now, an isolated semi-solid pool and on-resonance RF-irradiation, the transversal components $$$x,y$$$ of the Bloch equations6 are formally solved as follows:$$x(t)=\int_0^tG(t,\tau)\omega_y(\tau)z(\tau)d\tau$$$$y(t)=-\int_0^tG(t,\tau)\omega_x(\tau)z(\tau)d\tau,$$where$$G(t,\tau)=\exp(-(t-\tau)/T_2)\;\;\forall\;\;t\geq\tau$$is Green's function, which describes the free induction decay (FID). Physically, we can interpret this solution by splitting the RF-field $$$\omega_{x,y}$$$ into infinitesimally short pulses: each hard pulse at the time $$$\tau$$$ excites transversal magnetization, which, thereafter, decays freely before it is observed at the time $$$t$$$.

It is well known that semi-solid spin pools exhibit non-Lorentzian lineshapes, such as the super-Lorentzian.7,8 As shown by Ernst et al., the FID is, under certain circumstances, equivalent to the Fourier transform of the corresponding lineshape.9,10 Therefore, we make the ansatz that we can replace the Green's function with the Fourier transform of, e.g., the super-Lorentzian lineshape:$$G(t,\tau)=\int_0^{1}\exp\left(-(t-\tau)^2/T_2^2\cdot\frac{(3\zeta^2-1)^2}{8}\right)d\zeta.$$Inserting this Green's function into above solution of the Bloch equations facilitates the description of the spin dynamics in the semi-solid pool during RF-pulses.

As the semi-solid pool's transversal magnetization decays before we can measure it with common clinical pulse sequences, one is often interested only in its implicit effect on the longitudinal magnetization. Hence, we can insert above derived generalized Bloch equations into the regular Bloch equation that describes the evolution of the $$$z$$$-magnetization$$\partial_t z(t)=-\omega_y(t)\int_0^tG(t,\tau)\omega_y(\tau)z(\tau)d\tau-\omega_x(t)\int_0^tG(t,\tau)\omega_x(\tau)z(\tau)d\tau+(1-z(t)/T_1).$$and solve this differential equation numerically. We note that the transverse magnetization is implicitly baked into this equation, and the multiplications of $$$z(\tau)$$$ with $$$\omega_{x,y}(\tau)$$$ and $$$\omega_{x,y}(t)$$$ describe rotations.

The generalized Bloch equations can be incorporated in a Bloch-McConnell equation11 to describe the transfer of $$$z$$$-magnetization between the semi-solid and the free pool.

Methods

Simulations: We performed MT simulations during continuous waves and rectangular RF-pulses, assuming a Lorentzian lineshape (for which the original Bloch equation yields ground truth behavior), or a super-Lorentzian lineshape (for which no such ground truth exists). For comparison, we also simulate Graham's3 and Sled's4 models. Note that Graham's model is not valid for a super-Lorentzian lineshape and on-resonant RF-pulses due to the divergence of the lineshape.

Experiments: We performed inversion recovery experiments12 with varying inversion-pulse durations on a 1T NMR spectrometer. We scanned thermally cross-linked bovine serum albumin (BSA), where the BSA makes up 15% of the overall sample weight, and fitted Sled's and the generalized Bloch model to the data.

Results

As expected from theory, generalized-Bloch simulations during a continuous RF-wave show good agreement with Henkelman's steady-state model and with the original Bloch model when assuming a Lorentzian lineshape (Fig. 2). Sled's model, however, deviates from the generalized Bloch model: while the former describes a decay of $$$z$$$-magnetization, the latter captures the RF-induced rotation of the magnetization—similar to the Bloch model—which results here in a negative $$$z$$$-magnetization in the time span $$$t\gtrapprox1$$$ms.

The agreement between the generalized Bloch model with a Lorentzian lineshape and the original Bloch model is confirmed by simulations of the spin dynamics evoked by RF-pulses (left column of Fig. 3). Fig. 3 further shows good agreement between all described models for long RF-pulse durations ($$$T_\text{RF}\gg\;T_2$$$). However, the figure also demonstrates that all established models fail to describe the expected rotation induced by short RF-pulses ($$$T_\text{RF}\ll\;T_2$$$). In this limit, the pulse instantaneously rotates all magnetization and we expect $$$z(T_\text{RF})=z(0)\cos\alpha$$$. In contrast, the generalized Bloch model describes such spin dynamics adequately.

Experimentally, we find that short $$$T_\text{RF}$$$ pulses indeed invert the semi-solid pool, which results in a mono-exponential inversion recovery curve (Fig. 4). In contrast, long $$$T_\text{RF}$$$ pulses induce a bi-exponential decay.12 We fitted the data with the Bloch-McConnell model, where the semi-solid pool was described with Sled's or the generalized Bloch model, and observed a much better fit with the latter. Further, the parameters estimated with the generalized Bloch model (Tab. 1) are in line with literature, while we observe unrealistically short $$$T_2^\text{semi-solid}$$$ values for Sled's model.

Discussion and Conclusion

We have presented a generalization of the Bloch model to non-exponential decays or, equivalently, to non-Lorentzian lineshapes. From a theoretical perspective, this model has the advantage over existing MT models3,4 that it unifies the original Bloch model and Henkelman's steady-state model, while also adequately describing the rotation induced by short RF-pulses.5 Experimentally, we observe an improved fit with the generalized Bloch model. The deviation of the generalized Bloch model from existing models is most pronounced for short RF pulses, while all models show good agreement for long RF pulses. An in vivo application of this model will be demonstrated elsewhere.

Acknowledgements

This work was supported by grant NIH/NIBIB R21 EB027241 and was performed under the rubric of the Center for Advanced Imaging Innovation and Research, a NIBIB Biomedical Technology Resource Center (NIH P41 EB017183).

References

  1. SD Wolff and RS Balaban. Magnetization transfer contrast (MTC) and tissue water proton relaxation in vivo. Magn. Reson.2 Med., 10(1):135–144, 1989.
  2. RM Henkelman, X Huang, QSS Xiang, GJ Stanisz, SD Swanson, and MJ Bronskill. Quantitative Interpretation of Magnetization Transfer. Magn. Reson. Med., 29(6):759–766, 1993.
  3. SJ Graham and RM Henkelman. Understanding pulsed magnetization transfer. J. Magn. Reson. Imaging, 7(5):903–912, 1997.
  4. JG Sled and GB Pike. Quantitative Interpretation of Magnetization Transfer in Spoiled Gradient Echo MRI Sequences. J. Magn. Reson., 145(1):24–36, 2000.
  5. AP Manning, AL MacKay, and CA Michal. Understanding aqueous and non-aqueous proton T1 relaxation in brain. J. Magn. Reson., 323:106909, 2021.
  6. F Bloch. Nuclear induction. Phys. Rev., 70(7-8):460–474, 1946.
  7. H Wennerström. Proton nuclear magnetic resonance lineshapes in lamellar liquid crystals. Chem. Phys. Lett., 18(1):41–44, 1973.
  8. C Morrison and RM Henkelman. A Model for Magnetization Transfer in Tissues. Magn. Reson. Med., 33(4):475–482, 1995.
  9. RR Ernst and WA Anderson. Application of Fourier Transform Spectroscopy to Magnetic Resonance. Rev. Sci. Instrum., 37(1):93–102, 1966.
  10. RR Ernst, WP Aue, E Bartholdi, A Höhener, and S Schäublin. Equivalence of Fourier Spectroscopty and Slow Passage in Nuclear Magnetic Resonance. In Mol. Spectrosc., number iii, pages 47–60. Elsevier, 1974.
  11. HM McConnell. Reaction Rates by Nuclear Magnetic Resonance. J. Chem. Phys., 28(3):430–431, 1958.
  12. DF Gochberg and JC Gore. Quantitative imaging of magnetization transfer using an inversion recovery sequence. Magn. Reson. Med., 49(3):501–505, 2003.
  13. GJ Stanisz, EE Odrobina, JPM Escaravage, SJ Graham, MJ Bronskill, and RM Henkelman. T1, T2 relaxation and magnetization transfer in tissue at 3T. Magn Reson Med, 54(3):507–512, 2005.

Figures

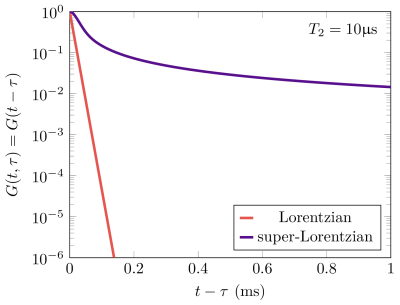
Fig. 1: Green's Functions associated with Lorentzian or super-Lorentzian lineshapes. They are given by the Fourier transform of the respective lineshape and are equivalent to the FID after excitation with a hard RF-pulse (assuming T2* = T2). Despite having the same T2 = 10μs, the decay characteristics of the two functions differ substantially: while the magnetization associated with the Lorentzian lineshape decays exponentially, i.e. linearly in this log-plot, the super-Lorentzian Green's function flattens due to long-lived components.

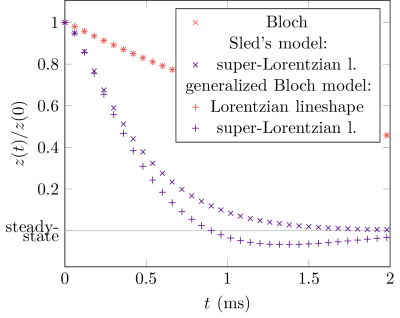
Fig. 2: Simulated dynamics of an isolated semi-solid pool during a continuous RF-wave. As predicted by theory, we observe good agreement between the generalized Bloch and Henkelman's model for the case of a steady state, as well as between the generalized Bloch model with a Lorentzian lineshape and the original Bloch model. A comparison to Sled's theory reveals deviations between the two models. The horizontal line indicates the steady-state predicted by Henkelman's theory. The simulations were performed with T2 = 10μs, T1 = 1s, Δ/(2π) = 100Hz, and ω1/(2π) = 1000Hz.

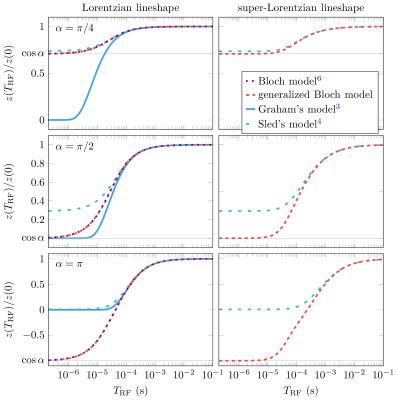
Fig. 3: Simulated z-magnetization of an isolated semi-solid pool at the end of an RF-pulse. For a Lorentzian lineshape, we observe good agreement between the generalized Bloch and the original Bloch model. For either lineshape, we observe good agreement between all models at long pulse durations (TRF); for short RF-pulses, however, only the generalized Bloch model describes the known rotation of the magnetization so that z(TRF)/z(0) = cos α, where α denotes the flip angle. Graham's model could not be simulated for the super-Lorentzian lineshape due to its singularity on resonance.

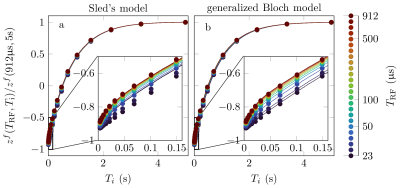
Fig. 4: Inversion recovery NMR experiment for a bovine serum albumin (BSA) sample with different inversion pulse durations TRF and different inversion times Ti. The data is well-described by the generalized Bloch model, and the details of the fit are superior to those using Sled's model. The fitted parameters are shown in Tab. 1.

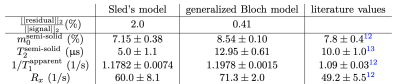
Tab. 1: Parameters of a bovine serum albumin (BSA) sample, which are estimated by fitting either Sled's model or the generalized Bloch model to the data, juxtaposed to selected parameter values reported in the literature. Note, however, that the values reported here for various models cannot be compared directly to the literature values, as different samples and experimental conditions were used.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)
2707
DOI: https://doi.org/10.58530/2022/2707