2702
Nanoscopic materials for quantitative water exchange phantoms1Radiology, University of Michigan, Ann Arbor, MI, United States
Synopsis
Nanoparticle lipid vesicles are developed with controllable water exchange to provide a ground-truth benchmark for MR methods which measure exchange. Diffusion data are collected as a function of diffusion delay Δ. An exchange time, τ, is measured to be 164 ms in a phantom with a highly fluid membrane. These materials should help to clarify water dynamics in complex systems.
Introduction
Water exchange between compartments can be measured by examining the diffusion decay curve as a function of diffusion delay Δ (1,2). Changes in tissue cellularity in vivo in cancer lesions affect stochastic water motions and lead to changes in time dependent water diffusion (3,4). In addition, time dependent diffusion in white matter reveals a novel structural contrast on a micrometer scale (5) and exchange of axonal and myelin water influences steady-state methods to measure myelin content (6).We present here examples of chemical phantoms with controllable water exchange to provide a ground-truth benchmark for MR methods to measure exchange and to clarify water dynamics in complex systems.
Methods
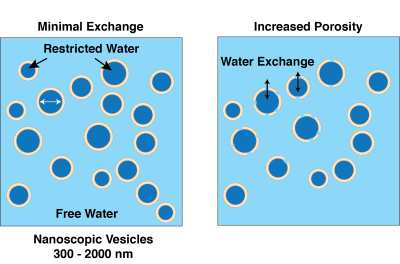
Chemical Compositions: As with our previous diffusion-kurtosis phantoms (7), nanoscopic vesicles were made with a combination of alcohols and surfactants. A phantom with minimal water exchange (on the time-scale of the diffusion experiment ) was made with high molecular weight Cetearyl alcohol (a combination of C16 cetyl alcohol and C18 stearyl alcohol), Stearylamidoproply dimethylamine, and Behentrimonium chloride (Sample CSB, Fig. 1- left panel). The high molecular weight alcohols (melting point 52 °C) create a relatively impenetrable barrier for water exchange at room temperature. The CSB sample had solid content of 0.5% and a restricted diffusion water fraction of approximately 9%.Lower molecular weight alcohols and surfactants were used o create a phantom with water exchange on the diffusion experiment time-scale. Specifically, 1-decanol and cetyltrimonium bromide (CTAB) (dec-CTAB, Fig. 1 right panel) were combined at 1:1 weight ratio and total solid content 1.5%. Decyl alcohol is a liquid at room temperature (melting point 6.4 °C) and makes a fluid membrane structure, allowing the water to move from the restricted diffusion vesicles to the free water pool.
Diffusion Measurements: NMR studies were performed at 16.4T and 25 °C on a Varian/Agilent system using a stimulated echo diffusion sequence with convection compensation. Diffusion decay curves were obtained with δ = 5ms and Δ varied from 20 ms to 4 s. Gradient amplitudes were adjusted to obtain b values in each experiment up to about 10,000 s/mm2.
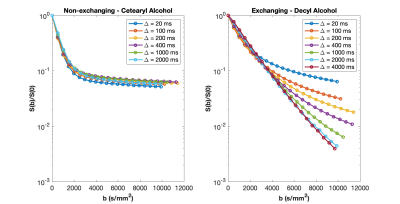
Diffusion decay data for non-exchanging CSB and exchanging dec-CTAB are shown in Figs. 2a and 2b, respectively.
Results
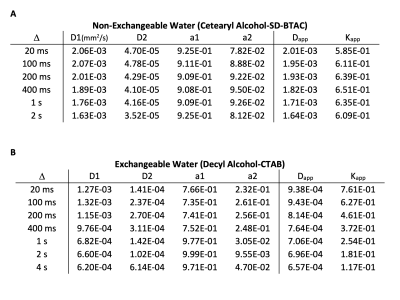
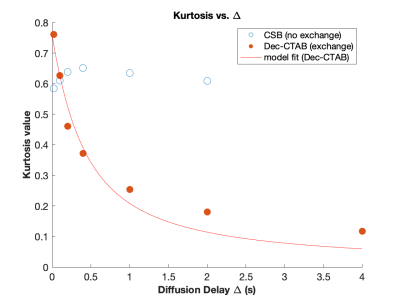
Data was analyzed with a two-component biexponenal model, $$$S(b)/S(0)=a_1 exp(-D_1 b) +a_2 exp(-D_2 b)$$$, and with a Diffusion-Kurtosis model, $$$ln[S(b)/S(0)]=-D_{app} b +1/6 K_{app}(D_{app} b)^2$$$, at appropriate b values. Results of the fitting the data of the CSB sample and dec-CTAB sample are shown in Table 1A and 1B, respectively.Kurtosis values of Dec-CTAB as a function of increasing Δ were fitted to a Karger model for water exchange (8), $$$K(t) = K_0 \frac{2 \tau}{\Delta}[1-\frac{\tau}{\Delta} (1-exp(-\Delta/\tau)]$$$, where $$$\tau$$$ is the water exchange time. Kurtosis values as a function of diffusion delay Δ for CSB and dec-CTAB are shown in Fig. 3. In addition the fitted Karger model is shown for the exchangeable dec-CTAB sample. The water exchange time in the dec-CTAB sample is estimated to be $$$\tau = 164 ± 82 ms$$$. The average kurtosis value for the CSB sample is 0.62 ± 0.02 for all values of Δ.
Discussion
CSB (non-exchanging): The diffusion decay curve presented in Fig. 2 for the CSB sample is similar for all values of Δ. There is some variation in the Kurtosis values, but this is may be due to water finding more barriers during the diffusion delay. The mean free path of free water is 8 μm at 20 ms and 90 μm at 2 s, a much longer distance for water to be impeded. On average, kurtosis is 0.62 ± 0.02 for the CSB sample. The size of the restricted diffusion pool (a2) is relatively constant at about 9%. The high molecular weight CSB sample is relatively insensitive to Δ, a desirable property for a diffusion-kurtosis phantom.Dec-CTAB (exchanging): A much different picture emerges in the low molecular weight sample. At Δ = 20 ms, a snapshot of diffusive behavior is recorded revealing high kurtosis (0.76). Kurtosis decreases as Δ increase because the free and restricted pools are averaged. The snapshot becomes a time-averaged blurred picture of water motion. At Δ = 20 ms, the two-pool biexponential model reveals 77% and 23% for free and restricted diffusion. At Δ = 2 s, the two pools merge into one pool with an averaged diffusion constant. Kurtosis in dec-CTAB also decreases dramatically from 0.76 at Δ = 20ms to 0.11 at Δ = 4s.
Conclusion
We present here two chemical phantoms based on nanoparticle lipid vesicles with either no water exchange (on the time-scale of diffusion MRI ) or with water exchange with a time constant τ of 164 ms. In vivo, exchange between intracellular and extracellular water is controlled by aquaporin proteins. In the phantom materials, exchange is controlled by the fluidity of the lipid membrane. Future work will develop membrane systems with tunable exchange times to be used as a ground-truth physical item to test and calibrate advanced imaging methods and gain a deeper understanding of water diffusion in vivo.Acknowledgements
Support for this project was provided by the US NIH through grants U01CA211205, and 75N91021C00036.References
1. Kärger J. NMR self-diffusion studies in heterogeneous systems. Adv Colloid Interface Sci. 1985;23:129–148.
2. Nilsson M, van Westen D, Stahlberg F, Sundgren PC, Latt J. The role of tissue microstructure and water exchange in biophysical modelling of diffusion in white matter. Magn Reson Mater Phys Biol Med. 2013;26(4):345–370.
3. Lemberskiy G, Rosenkrantz AB, Veraart J, Taneja SS, Novikov DS, Fieremans E. Time-dependent diffusion in prostate cancer. Invest Radiol. 2017;52(7):405–411. PMID: 28187006
4. Reynaud O. Time-dependent diffusion MRI in cancer: Tissue modeling and applications. Front Phys. 2017;5(NOV):1–16.
5. Fieremans E, Burcaw LM, Lee HH, Lemberskiy G, Veraart J, Novikov DS. In vivo observation and biophysical interpretation of time-dependent diffusion in human white matter. Neuroimage [Internet]. Elsevier Inc.; 2016;129:414–427. Available from: http://dx.doi.org/10.1016/j.neuroimage.2016.01.018 PMID: 26804782
6. Harkins KD, Dula AN, Does MD. Effect of intercompartmental water exchange on the apparent myelin water fraction in multiexponential T2 measurements of rat spinal cord. Magn Reson Med. 2012;67(3):793–800.
7. Malyarenko I D, Swanson SD, Konar AS, LoCastro E, Paudyal R, Liu MZ, Jambawalikar SR, Schwartz LH, Shukla-Dave A, Chenevert TL. Multicenter Repeatability Study of a Novel Quantitative Diffusion Kurtosis Imaging Phantom. TOMOGRAPHY. 2019 Mar;5(1):36–43.
8. Jensen JH, Helpern JA. MRI quantification of non-Gaussian water diffusion by kurtosis analysis. NMR Biomed. 2010;23(7):698–710.
Figures