Introduction

T1ρ-Mapping of knee cartilage has been shown to provide a good distinction between osteoarthritis patients and controls ^1,2. Several T1ρ-weighted images with different Spin-Lock Times are required to estimate the free parameters of the exponential models. The distribution of TSLs used can be optimized to improve the quality of the estimated parameters ^3,4. The Cramér-Rao Lower Bound (CRLB)⁵ can be used to find the best TSLs for different exponential models and #TSLs⁴. In this study, we extend the approach in ⁴ to stretched- and bi-exponential T1ρ mapping.

Methods

Mono-exponential models, commonly used for T1ρ quantification, are defined as:
$$x(t,n)=c(n)\exp\left(\frac{-t}{\tau(n)} \right),$$
where $$$x(t,n)$$$ denotes the complex-valued voxel at time $$$t$$$ and spatial position $$$n$$$, $$$c(n)$$$ is the complex-valued exponential coefficient and $$$\tau(n)$$$ is the time constant of decay. It has been shown that the mono-exponential model cannot fully represent the relaxation decays⁶, and so, more sophisticated models are needed for the cases where relaxation decay deviates from the simpler mono-exponential model.
Multiexponential models have been proposed, improving the characterization of cartilage^6,7. The bi-exponential model considers the sum of two mono-exponential models, with one being a short exponential and the other a larger exponential. It can be defined as:
$$x(t,n)=c(n) \left( f(n)\exp\left(\frac{-t}{\tau_l(n)} \right)+(1-f(n))\exp\left(\frac{-t}{\tau_s(n)}\right) \right),$$
in which\ $$$0 \leq f(n) \leq 1$$$ denotes the fraction corresponding to the longer exponential, $$$\tau_l(n)$$$ and $$$\tau_s(n)$$$ are the longer and shorter decay time constants, respectively.
The stretched-exponential model proposed by Johnston⁷ is defined as:
$$x(t,n)=c(n) \exp\left(-\left(\frac{t}{\tau^*(n)} \right)^{\beta(n)} \right),$$
Where $$$\tau^*(n)$$$ denotes the characteristic relaxation time and $$$\beta(n)$$$ denotes the stretching exponent.
The Cramér-Rao Matrix (CRM) main diagonal contains the CRLB for each parameter, i.e., the minimum possible variance that an unbiased estimator can achieve for the estimated parameters. It is defined as:
$$V(\mathbf{t},\bf \theta)= \left( E\left[\left(\frac{\partial \log \rho(\mathbf{t},\bf \theta)}{\partial \theta } \right)\left( \frac{\partial \log \rho(\mathbf{t},\bf \theta)}{\partial \theta } \right)^T|\mathbf{t},\theta \right] \right)^{-1},$$
Where $$$\mathbf{t}$$$ is a vector containing every TSL used, $$$\theta$$$ contains the free parameters, and $$$\rho$$$ is a Gaussian probability density function⁵.
Another approach is to consider a Modified CRLB (MCRLB), where each element in the main diagonal of the CRM is define as:
$$ \left[ V_m(\mathbf{t},\bf \theta) \right]_{i,i}= \frac{\sqrt{ | \left[ V(\mathbf{t},\bf \theta) \right]_{i,i} | } }{|\left[\theta \right]_i | },$$
We look for the $$$\bf{t}$$$ that produces the smallest weighted mean of diagonal elements across every $$$\theta$$$, as:
$$\bf{\hat{t}} = \arg\min_{\bf{t}\in T}\frac{1}{S}\sum^S_{s=1}\left(\sum_i\omega_i\left[\bf{V(t,\theta_S)}\right]_{i,i}\right)$$.
Also, the same minimizations can be done using $$$\bf{Vm}$$$, instead of $$$\bf{V}$$$, for obtaining the minimum MCRLB for each parameter.
Synthetic experiments were carried out for mono-, stretched- and bi-exponential models. For each model, the experiments were done considering minimization of the mean CRLBs and MCRLBs. The selection of $$$\bf{t}$$$ is made using Pareto Optimization for Subset Selection (POSS)⁸ and the validation is done with Non-Linear Least Squares (NLS) via the Conjugate Gradient Steihaug’s Trusted Region (CGSTR)⁹. The range of values used for validation are: $$$10\leq\tau\leq 70$$$, $$$0.05\leq f\leq 0.95$$$, $$$15\leq\tau_l\leq 100$$$, $$$0.1\leq\tau_s\leq 10$$$, $$$1\leq\tau^*\leq 70$$$ and $$$0.1\leq\beta\leq 1.0$$$.
For each model, a set of 100000 $$$\theta$$$ was randomly selected and used to synthesize the signal which was sampled at positions $$$\bf{\hat{t}}$$$. The signals were contaminated with Additive White Gaussian Noise (AWGN) to obtain a Signal-to-Noise Ratio (SNR) of 30dB. The set of $$$\hat{\theta}$$$ was estimated and the fitting errors were evaluated using a weighted mean of the Mean of the Normalized Absolute Error (MNAE) for each model parameter, the same weights used for finding $$$\bf{\hat{t}}$$$. The weighted mean MNAE is defined as:
$$ MNAE=\frac{1}{\vert N\vert}\sum_i\omega_i\left(\sum_{\bf{n}\in N}\frac{\vert \theta-\hat{\theta}\vert}{\vert \theta\vert}\right)$$.

Results and Discussion

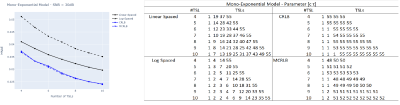
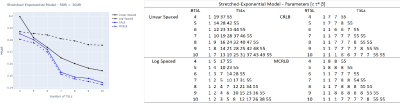
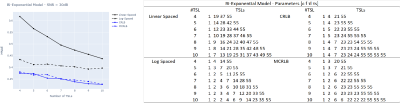
Figures 1, 2, and 3 illustrate the results obtained from Monte Carlo (MC) simulations of the three models with non-optimized and optimized TSLs. The figures also show tables detailing the TSL values used for each model with different #TSL.From these results, we conclude that the optimization targets TSLs that can help to distinguish the parameters. For instance, in the Bi-Exponential model, shorter TSLs are required to estimate $$$\tau_s$$$ and so, the optimization leads to the selection of some TSLs in the lower range, and even the repetition some (MCRLB with #TSL=10). Also, the repetition of TSLs in the higher end of the range is a way of reducing noise where the signal is weaker, which improves the SNR and, as a consequence, the estimation. The optimized TSLs lead to smaller errors in each scenario.
Another takeaway is that the MCRLB, as an optimization criterion, seems to lead to a more robust set of TSLs. Figures 1 and 2 show that, although the results can be very close, the errors were smaller for the MCRLB. In Figure 3, it is unclear which is best as the curves oscillate.
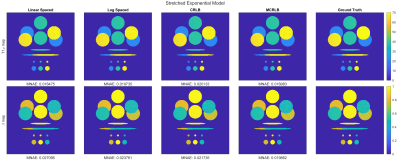
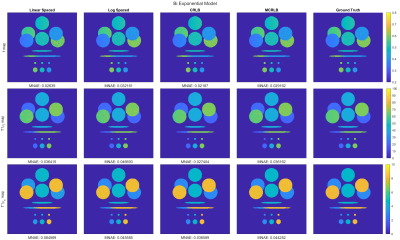
We also evaluated the performance of the optimized TSLs using Synthetic model phantoms. The estimated parameters maps for the stretched- and bi-exponential models are shown in Figure 4 and Figure 5, respectively. The results are consistent with what was observed previously, the use of optimized TSLs led to parameter maps with lower errors than those obtained using non-optimized TSLs.

Acknowledgements

This work was supported in part by NIH grants R01-AR067156, R01-AR068966, and was performed under the rubric of the Center for Advanced Imaging, Innovation and Research (CAI2R, www.cai2r.net) an NIBIB Biomedical Technology Resource Center (NIH P41 EB017183).

References

1. Regatte RR, Akella SVS, Lonner JH, Kneeland JB, Reddy R. T1ρ relaxation mapping in human osteoarthritis (OA) cartilage: Comparison of T1ρ with T2. J Magn Reson Imaging. 2006;23(4):547-553. doi:10.1002/jmri.20536

2. MacKay JW, Low SBL, Smith TO, Toms AP, McCaskie AW, Gilbert FJ. Systematic review and meta-analysis of the reliability and discriminative validity of cartilage compositional MRI in knee osteoarthritis. Osteoarthr Cartil. 2018;26(9):1140-1152. doi:10.1016/j.joca.2017.11.018

3. Johnson CP, Thedens DR, Magnotta VA. Precision-guided sampling schedules for efficient T1ρ mapping. J Magn Reson Imaging. 2015;41(1):242-250. doi:10.1002/jmri.24518

4. Zibetti MVW, Sharafi A, Regatte RR. Optimization of spin‐lock times in T1ρ mapping of knee cartilage: Cramér‐Rao bounds versus matched sampling‐fitting. Magn Reson Med. 2021;(April):1-17. doi:10.1002/mrm.29063

5. Kay SM. Fundamentals of Statistical Signal Processing: Estimation Theory. Prentice Hall; 1993.

6. Reiter DA, Magin RL, Li W, Trujillo JJ, Pilar Velasco M, Spencer RG. Anomalous T 2 relaxation in normal and degraded cartilage. Magn Reson Med. 2016;76(3):953-962. doi:10.1002/mrm.25913

7. Johnston DC. Stretched exponential relaxation arising from a continuous sum of exponential decays. Phys Rev B. 2006;74(18):184430. doi:10.1103/PhysRevB.74.184430

8. Qian C, Yu Y, Zhou ZH. Subset selection by Pareto optimization. In: Advances in Neural Information Processing Systems. Vol 2015-Janua. Advances in Neural Information Processing Systems. ; 2015:1774-1782.

9. Steihaug T. The conjugate gradient method and trust regions in large scale optimization. SIAM J Numer Anal. 1983;20(3):626-637. doi:10.1137/0720042