2688

Hybrid PCA denoising - improving PCA denoising in the presence of spatial correlations

Rafael Neto Henriques¹, Sune Nørhøj Jespersen^2,3, and Noam Shemesh¹
¹Champalimaud Research, Champalimaud Centre for the Unknown, Lisbon, Portugal, ²Center of Functionally Integrative Neuroscience (CFIN) and MINDLab, Clinical Institute, Aarhus University, Aarhus, Denmark, ³Department of Physics and Astronomy, Aarhus University, Aarhus, Denmark

Synopsis

PCA denoising based on the Marchenko-Pastur (MP) distribution has become the state-of-the-art procedure to suppress thermal noise in multi-dimensional MRI. Here we developed a Hybrid-PCA strategy that combines a-priori noise variance estimation and the random matrix theory for PCA eigenvalue classification, to overcome shortcomings of contemporary MP-PCA denoising. Our results show that, while the MP-PCA denoising fails to classify the noise PCA components in data with spatially correlated noise, the Hybrid-PCA algorithm maintains its denoising performance. The Hybrid-PCA denoising can thus be a useful procedure for data corrupted by spatially correlated noise, as typically arises in vendor reconstructed data.

Introduction

PCA denoising has become the state-of-the-art procedure to suppress thermal noise in multidimensional MRI acquisitions since it was shown to provide an optimal compromise between noise suppression and preservation of structural information^1-4. This technique involves removal of noise PCA components which can be classified by using empirical thresholds¹ or assuming that the eigenvalue of these components follows specific distributions^2-4. For instance, assuming that noise eigenvalues are characterized by a Marchenko-Pastur distribution⁵, Veraart et al. proposed an objective PCA component classification based on a moment matching algorithm². While this technique has become one of the most employed denoising strategies in MRI, its performance is suboptimal for data corrupted by spatially correlated noise. Here, we evaluate the influence of spatial correlations on MP-PCA denoising, and then develop the Hybrid-PCA denoising strategy that combines a-priori noise variance estimation and random matrix theory, to overcome the shortcomings of contemporary PCA denoising procedures.

Theory

MP-PCA denoising: According to Marchenko and Pastur^2,5, Gaussian noise with variance $$$\sigma$$$ propagated from a $$$M\times N$$$ matrix to the PCA eigenvalues $$$\lambda$$$ has the following probability distribution:$$p(\lambda)=\left\{\begin{matrix}\frac{\sqrt{(\lambda_+-\lambda)(\lambda-\lambda_-)}}{2\pi\vartheta\lambda\sigma^2}& & if & \lambda_-<\lambda<\lambda_+ \\ 0 & & &otherwise\end{matrix}\right.\;\;\;\;\;\;(Eq. 1)$$with $$$\lambda_\pm=\sigma^2(1\pm\sqrt{\vartheta})^2$$$ and $$$\vartheta=N/M$$$. In the original MP-PCA algorithm, noise-related eigenvalues are classified as the maximum number of smallest eigenvalues that best fits the above probability distribution. This can be achieved by iteratively removing the larger eigenvalues until the following inequality is satisfied²:$$\widehat{\omega}\leq 4\overline{\lambda_c}\sqrt{\frac{C}{M}}\;\;\;\;\;\;\;\;\;\;(Eq. 2)$$where $$$\widehat{\omega}$$$ is the estimated distribution bandwidth, $$$\overline{\lambda_c}$$$ is the mean of selected eigenvalues, and $$$C$$$ the number of selected eigenvalues.

Hybrid-PCA denoising: According to random matrix theory, the mean of noise components $$$\overline{\lambda}$$$ is equal to $$$\sigma^2$$$ Thus, an alternative to the MP-PCA procedure is to classify noise components by selecting the larger number of components that satisfies the following inequality:$$\overline{\lambda_c}\leq\widehat{\sigma}^2\;\;\;\;\;\;\;\;\;\;(Eq. 3)$$This latter strategy is here referred to as Hybrid-PCA since it combines random matrix concepts with a noise variance estimate $$$\widehat{\sigma}^2$$$. Here $$$\widehat{\sigma}^2$$$ is calculated from the MRI data repetitions acquired with no diffusion sensitization. Note that this procedure is more general than MP-PCA denoising since it does not rely on a specific propability distribution.

Methods

Simulations: Diffusion-weighted signals of synthetic phantom with 12×12 “voxels” were generated for 45 gradient directions for b-values 1 and 2 ms/μm², 20 b-value=0 instances and assuming a two-compartmental model (compartments with axial diffusivities of 1.8 μm²/ms and 1.5 μm²/ms and radial diffusivities of 0 and 0.5 μm²/ms). The phantom were divided in nine portions and signals for each portion were generated for its own compartments' main direction and volume fractions. Phantoms are corrupted by Rician noise with SNR(b0)=50. Spatial correlated noise was generated by smoothing the noisy phantoms (2D kernel with standard deviation of 0.6).

MRI experiments: All animal experiments were preapproved by the institutional and national authorities and carried out according to European Directive 2010/63. MRI experiments of an ex vivo mouse brain (C57BL/6J) were performed on a 16.4 T Bruker Aeon scanner. Two different datasets were acquired using Bruker’s standard “DTI EPI” sequence:
1) acquisitions with parameters optimized to minimize noise spatial correlations - no acquisition during EPI’s gradient ramp (i.e. ramp compensated) and no partial Fourier factor);
2) acquisition with parameters optimized for acceleration - acquisition starting at the beginning of gradient ramps (default Bruker’s procedure for acquisition speed) and with partial Fourier factor = 1.4.

Both datasets were acquired along 30 diffusion gradient directions for b-values 1, 2 and 3 ms/μm² (Δ=15 ms, δ=1.5 ms) and for 20 b-value=0 repetitions. The performance of the denoising algorithms is assessed directly on diffusion-weighted data, and we also analyze their impact on DKI reconstruction^6,7.

Results

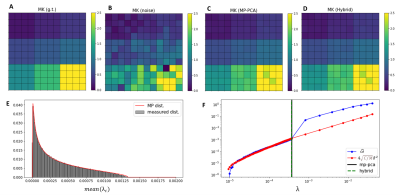
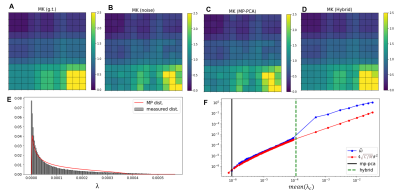
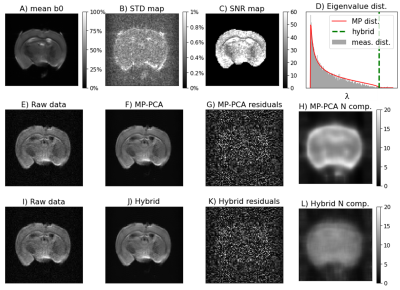
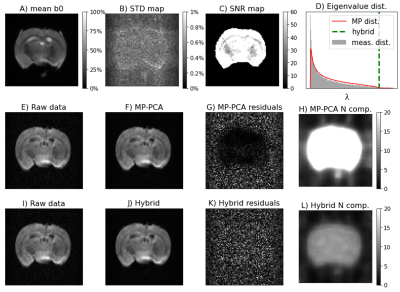
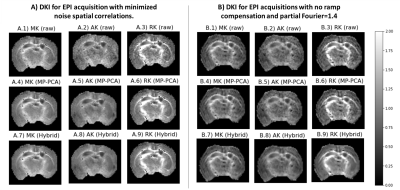
Simulations: Noise effects are visualized on mean kurtosis maps for phantoms corrupted with spatially uncorrelated and correlated noise in Fig. 1A-D and Fig. 2A-D respectively. For spatially uncorrelated noise, MP-PCA denoising stopping criterion ($$$\widehat{\omega}\leq 4\overline{\lambda_c}\sqrt{C/M}$$$) is satisfied when the nine ground truth signal components are not classified as noise components (Fig. 1E); however, it fails to converge for spatially correlated noise (Fig. 2E). On the other hand, the Hybrid-PCA denoising successfully classifies the nine signal components for both phantoms (Fig. 1E, Fig. 2E).

MRI experiments: The denoising performance of Hybrid-PCA is similar to MP-PCA for data acquired with parameters optimized to minimize noise spatial correlations (Fig.3). However, the MP-PCA procedure fails to denoise the data acquired with no EPI ramp compensation and partial Fourier of 1.4 (Fig.4). DKI maps before and after denoising for both datasets are shown in Fig. 5.

DISCUSSION & CONCLUSION

While MP-PCA procedure is robust to some degree of spatially correlated noise (e.g effects of EPI gridding for dataset 1, Fig. 3), it fails to denoise data highly corrupted with spatially correlated noise (case of dataset 2 which was acquired with a high partial Fourier factor and was not ramp compensated, Fig. 4). Here, we show that PCA denoising strategies with better robustness to spatially correlated noise can be obtained by modifying the PCA component classification (Fig. 2). Particularly, by incorporating prior information of noise variance, our novel Hybrid-PCA approach maintains its denoising performance even on data strongly corrupted with spatially correlated noise (Figs. 4-5). These results are promising for enhancing the spatial and temporal resolution of MRI data on futures studies.

Acknowledgements

This study was funded by the European Research Council (ERC) (agreement No. 679058). We acknowledge the vivarium of the Champalimaud Centre for the Unknown, a facility of CONGENTO financed by Lisboa Regional Operational Programme (Lisboa 202), project LISBOA01-0145-FEDER-022170.

References

1. Manjón J V., Coupé P, Concha L, Buades A, Collins DL, Robles M. Diffusion Weighted Image Denoising Using Overcomplete Local PCA Gong G, editor. PLoS One 2013;8:e73021 doi: 10.1371/journal.pone.0073021.

2. Veraart J, Novikov DS, Christiaens D, Ades-aron B, Sijbers J, Fieremans E. Denoising of diffusion MRI using random matrix theory. Neuroimage 2016;142:394–406 doi: 10.1016/j.neuroimage.2016.08.016.

3. Does MD, Olesen JL, Harkins KD, et al. Evaluation of principal component analysis image denoising on multi-exponential MRI relaxometry. Magn. Reson. Med. 2019;81:3503–3514 doi: 10.1002/MRM.27658.

4. Bazin P-L, Alkemade A, van der Zwaag W, Caan M, Mulder M, Forstmann BU. Denoising High-Field Multi-Dimensional MRI With Local Complex PCA. Front. Neurosci. 2019;0:1066 doi: 10.3389/FNINS.2019.01066.

5. Marčenko VA, Pastur LA. Distribution of eigenvalues for some sets of random matrices. Math. USSR-Sbornik 1967;1:457–483 doi: 10.1070/SM1967V001N04ABEH001994.

6. Jensen JH, Helpern JA, Ramani A, Lu H, Kaczynski K. Diffusional kurtosis imaging: the quantification of non-gaussian water diffusion by means of magnetic resonance imaging. Magn. Reson. Imaging 2005;53 doi: 10.1002/mrm.2050

7. Henriques RN, Correia MM, Marrale M, et al. Diffusional Kurtosis Imaging in the Diffusion Imaging in Python Project. Front. Hum. Neurosci. 2021;0:390 doi: 10.3389/FNHUM.2021.675433.8.

Figures

Fig. 1 – Simulations with uncorrelated noise. (A) MK ground truth. (B) MK of noise corrupted phantoms. (C) MK of MP-PCA denoised data. (D) MK of Hybrid-PCA denoised data. (E) Measured eigenvalue distribution (grey bars) vs reference Marchenko-Pastur distribution for the same noise variance (red curve). (F) MP-PCA stopping criteria parameters plotted as a function of the mean of the eigenvalues classified as noise (MP and Hybrid PCA final thresholds are marked by vertical lines). This figure shows that MP-PCA stopping criteria is satisfied (c.f. Eq. 2) when data has uncorrelated noise.

Fig. 2 – Simulations with correlated noise. (A) MK ground truth. (B) MK of noise corrupted phantoms. (C) MK of MP-PCA denoised data. (D) MK of Hybrid-PCA denoised data. (E) Measured eigenvalue distribution (grey bars) vs reference MP distribution for the same noise variance (red curve). (F) MP-PCA stopping criteria parameters plotted as a function of the mean of the eigenvalues classified as noise (MP and Hybrid PCA final thresholds are marked by vertical lines). This figure shows that MP-PCA stopping criteria fails to converge when eigenvalues do not follow a MP distribution.

Fig. 3 - Denoising performance on EPI acquisitions with minimized noise spatial correlations. (A) mean b-value=0 image. (B) estimated noise standard deviation. (C) SNR(b0) map. (D) Measured eigenvalue distribution (grey bars) vs reference Marchenko-Pastur distribution for the same noise variance (red curve). For a representative diffusion-weighted image acquired for b-value = 3ms/µm², the following panels show: (E, I) the raw image; (F, J) denoised image; (G, K) denoising residuals; and (H, L) number of components preserved by the denoising strategies.

Fig. 4 - Denoising performance on EPI acquisitions with no ramp compensation and partial Fourier=1.4. (A) mean b-value=0 image. (B) estimated noise standard deviation. (C) SNR(b0) map. (D) Measured eigenvalue distribution (grey bars) vs reference Marchenko-Pastur distribution for the same noise variance (red curve). For a representative diffusion-weighted image acquired for b-value = 3ms/µm², the following panels show: (E, I) the raw image; (F, J) denoised image; (G, K) denoising residuals; and (H, L) number of components preserved by the denoising strategies.

Fig. 5 – DKI metrics for a representative slice for data acquired with minimized noise spatial correlations (A) and data acquired with partial Fourier of 1.4 and no ramp compensation (B). Note that, while noise effects on dataset 1 are substantially suppressed by both MP-PCA and Hybrid-PCA algorithm, noise effects on dataset 2 are only suppressed by the Hybrid-PCA algorithm. Noise suppression is more evident for axial kurtosis (AK) maps than for the mean kurtosis (MK) and radial kurtosis (RK) maps.

Proc. Intl. Soc. Mag. Reson. Med. 30 (2022)

2688

DOI: https://doi.org/10.58530/2022/2688