2632
Analytical Evaluation of Radio-Frequency Energy-Induced Heating in a Hot Spot without perfusion1Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany, 2Université Paris-Saclay, CEA, CNRS, BAOBAB, NeuroSpin, Gif-Sur-Yvette, France
Synopsis
We derived analytical steady-state and transient solutions for a sphere and a SAR source with uniform and the Gaussian distribution located in an infinite medium of homogeneous properties. The results obtained analytically showed that even without taking into account blood perfusion (i) if power deposition is present only in a sphere that encloses 10 gram of human tissue and SAR10g=10W/kg the steady-state temperature rise is below 3°C for power deposition distributions as sharp as Gaussian with σ=R/3=4.33mm, (ii) the sharper the Gaussian distribution of power deposition, the higher Tmax(t=+∞) and the faster it will approach steady-state.
Introduction
The specific absorption rate (SAR) averaged over the mass of 10 gram human tissue and over a 6 minute time (SAR10g) is the primary safety limit for 7T MRI scanners 1. SAR10g is also the safety limit for multi modal study, i.e., a combination of MRI with another technique, for example transcranial electric stimulation (tES) or electroencephalography (EEG), if additional equipment is entered into the effective exposure volume of the MRI radio-frequency (RF) coil. Especially in the latter case, locations with the highest RF power deposition, i.e., hot spots, in a human body can be substantially separated in space. The dimension of volume that consists of 10 gram human tissue is 21.55 mm as cube edge or 13.365 mm as sphere radius for most human tissues. Radius of a hot spot of substantial amount of active and passive implants is in a range from 1 mm till 15 mm. Radio-frequency energy-induced heating in human tissues is a very complex process with large influence of blood perfusion that in most cases decrease the level of heating. Thus heating estimation without blood perfusion results in a conservative value. Here we provide transient analytical solutions of the temperature rise for spherically symmetric SAR distributions (uniform and Gaussian).Methods
The heat diffusion equation without perfusion (as for instance the eyes) is defined as$$$ k\triangledown ^{2}T +{\rho}SAR={\rho}C\frac{\partial T}{\partial t} $$$ (1)
A sphere (S) of radius R enclosed in a second, infinite, sphere was considered. By symmetry, temperature only depends on the radial coordinate r if the SAR distribution itself is spherically symmetric.
If S is subjected to uniform SAR (SAR0) and there is no SAR outside of S the following steady-state differential equation (heat diffusion equation in spherical coordinates) is applicable:
$$$ k\frac{1}{r^{2}}\frac{\partial }{\partial r}(r^{2}\frac{\partial T}{\partial r})+{\rho}SAR_{0}=0 $$$ for r≤R (2)
$$$k\frac{1}{r^{2}}\frac{\partial }{\partial r}(r^{2}\frac{\partial T}{\partial r})=0$$$ for r>R (3)
As it is shown in Fig. 1 the solution for this problem at x=y=z=0 where maximum temperature occurs is
$$$ T_{max}=\frac{{\rho}SAR_{0}}{2k}R^{2} $$$ (4)
This is the same as equation 17 in 2. Analytical transient solutions in the center (maximum temperature in the sphere) likewise were obtained for uniform SAR by moving to the Fourier domain, integrating, and coming back to the spatial domain (Fig. 2):
$$$ T_{max}=\frac{{\rho}SAR_{0}}{2k}R^{2}\cdot(1-\sqrt{\frac{4{\alpha}t}{{\pi}R^{2}}}e^{-\frac{R^{2}}{4{\alpha}t}}-(1-2\frac{{\alpha}t}{R^{2}})\cdot{erf}(\frac{R}{2\sqrt{{\alpha}t}})) $$$ (5)
and for a SAR source with a Gaussian distribution (standard deviation of s, b is the SAR value at the center of the Gaussian) located in an infinite medium of homogeneous properties (Fig. 3)
$$$ T_{max}=\frac{{\rho}b\sigma^{2}}{k}\cdot(1-\frac{1}{\sqrt{1+\frac{2{\alpha}t}{\sigma^{2}}}}) $$$ (6)
These analytical solutions were compared to numerical solver results and showed perfect agreement. The time (t0.632) at which Tmax(t) will be equal to Tmax(t=+∞)×(1-e-1) for Gaussian distribution is
$$$t_{0.632}=(e^{2}-1)\frac{\sigma^{2}}{2\alpha}$$$ (7)
For the Gaussian case a function Tmax(t=+∞)×(1-e-t/t) can be used to approximate the solution at small times with a time constant $$$\tau=\frac{\sigma^{2}}{\alpha}=\frac{t_{0.632}}{3.195}$$$.
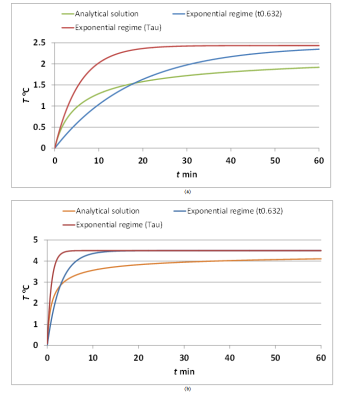
Please note, however, that the exact solution is not an exponential function so that the time it takes for the temporal part to decay to e-1 is in fact significantly longer because of the square root dependence in Eq. 6.
Results and Discussion
Assuming no perfusion, this work reports a conservative yet analytical evaluation of heating for uniform and Gaussian-shaped SAR hot spots. For uniform SAR of 10W/kg over 10g (13.4 mm radius sphere), and negligible SAR outside of S, Tmax is 1.78 °C (reached in about 22 minutes), which is reasonable considering temperature guidelines. Under the same assumptions, one can see in Eq. 5 that the steady-state temperature also grows with R2, i.e. with the size of the SAR hotspot, and linearly with the constant SAR0 value.Comparison between the transient values for the Gaussian case and the uniform one is presented in Fig. 4. When the energy outside of the 10g sphere is negligible, the more peaked the SAR distribution, the higher Tmax and the shorter τ. The difference between the exact analytical solution and an exponential regime with the same time-constants is highlighted in Fig. 5.
Conclusion
We showed analytically that even without taking into account blood perfusion (i) if power deposition is present only in a sphere that encloses 10 gram of human tissue and SAR10g=10W/kg the steady-state temperature rise is below 3 °C for power deposition distributions as sharp as Gaussian with s = R/3 = 4.45 mm, (ii) the sharper the Gaussian distribution of power deposition, the higher Tmax(t=+∞) and the shorter τ are.Acknowledgements
This work has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No 885876 (AROMA project).References
[1] Medical Electrical Equipment-Part 2–33: Particular Requirements for the Basic Safety and Essential Performance of Magnetic Resonance Equipment for Medical Diagnosis. International Electrotechnical Commission Standard 60601-2-33 Ed. 3, Geneva, Switzerland, 2010.
[2] K. R. Foster, A. Lozano-Nieto, and P. J. Riu. Heating of Tissues by Microwaves: A Model Analysis. Bioelectromagnetics, 19:420–428 (1998).
Figures



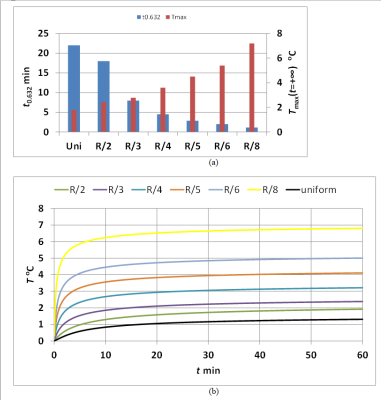
Fig. 4. Transient results at x=y=z=0 for a sphere of R=13 mm in radius for SAR averaged over the 10g sphere of 10W/kg with the Gaussian and the uniform distributions. (a) Time t0.632 and Tmax(t=+∞) for different SAR distributions over the sphere. (b) Temperature rise for uniform and Gaussian distributions with σ=R/2, σ=R/3, σ=R/4, σ=R/5, σ=R/6, σ=R/8.