Motivation

In MRI the acquired signal S(t) is given by: $$S(t)=∫[(M_T(x,y)∙exp\{-i[x∙k_x(t)+y∙k_y(t)]\}dxdy)],$$ where $$$M_T(x,y)$$$ is the transverse magnetization, which depends on excitation and refocusing flip angles. The image, reconstructed by a Fourier Transformation on the signal:
$$M_T(x,y)=∫[(S(k_x(t),k_y(t))∙exp\{i[x∙k_x(t)+y∙k_y(t)]\}dk_xdk_y)]\{1\}$$
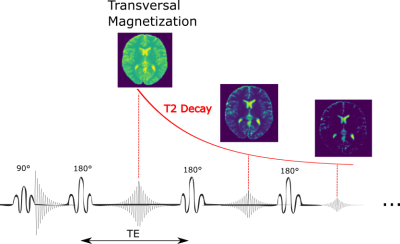
is proportional to the transverse magnetization at a certain time point. However, this concept is violated in fast imaging techniques like Turbo Spin Echo sequences, the short T2 values of different tissues are comparable to the echo-train duration, which results in significant T2 decay during k-space acquisition. Each echo along the phase encoding direction is collected at different time-points along the T2-decay curve (Fig.1). In FFT reconstruction, this leads to a voxel-T2-dependent k-space filter, which results in blurring or ringing. This filter can be described in the spatial domain by the Point-Spread-Function (PSF): $$\widetilde{M}(x,y)=M(x,y)*PSF(x,y)$$.
To solve the T2-blurring we need to tackle three different tasks:
(i) Sequence optimization: The effect of T2 decay during acquisition and contribution to the PSF can be reduced by using variable flip angles[1].
(ii) Generation of $$$M(x,y)$$$ and $$$\widetilde{M}(x,y)$$$ training samples. $$$M(x,y)$$$ at a certain time point cannot be measured directly, but is available in Bloch simulation when simulating $$$\widetilde{M}(x,y)$$$ using the sequence (i)
(iii) Training a deblurring CNN (Convolutional Neural Network) that forms a pseudo-inverse $$$M(x,y)=CNN(\widetilde{M}(x,y))$$$ using the uncorrupted target $$$M(x,y)$$$ of (ii)
In this work, we propose an end-to-end optimization approach to reduce T2 blurring in TSE sequences, by performing a joint optimization of sequence parameters (refocusing flip angles) and deblurring CNN using the actual transversal magnetization as target. Thus, we re-establish equation {1} for transient TSE sequences with complex voxel-T2-dependent PSF.

Material and Methods

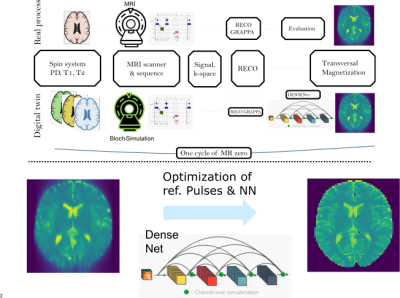
Signal simulations and optimization were performed using a Phase Distribution Graph (PDG) algorithm[2] implemented in the MRzero framework[3]. For maximal blurring, a single-shot 2D-TSE sequence (matrix:128x128, FOV:200mm, GRAPPA 3) was used with centric (TE_eff=20ms) and linear phase encoding reordering (TE_eff=320ms), respectively. The forward simulation outputs TSE images ($$$\widetilde{M}$$$) and transversal magnetization ($$$M(x,y)$$$), generated from synthetic brain samples based on the BrainWeb database[4] filled with in vivo-like tissue parameters. 20 subject volumes with 70 slices (1400 2D-TSE training samples) were used. MRzero optimizes the complete chain of sequence via differentiable Bloch simulation, reconstruction and CNN simultaneously (Fig.2). The optimized sequence parameters were the TSE refocusing flip angles and their phases; the CNN follows the DenseNet architecture[5]. A mean-squared-error loss is used with an additional loss for low signal intensity. The final sequences were exported with Pulseq[6] for in vivo measurements of a healthy subject at a Siemens Prisma 3T scanner using a 20ch head coil.

Results

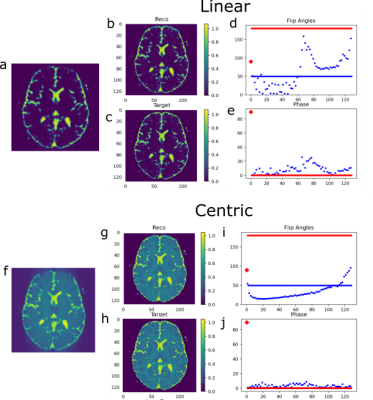
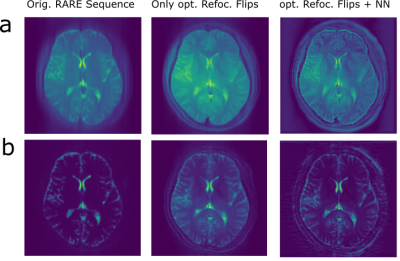
The final training stage with flip angle design and prediction on the simulation test set is shown in Figure 3. In the simulated centric TSE image with 180° flip angle train, blurring in phase encoding direction (anterior->posterior) is clearly visible (Fig.3f). The T2 blurring is strongly reduced by the CNN (Fig.3g), with sharp edges around the border of the brain and at tissue interfaces. Further, the overall contrast matches the target transversal magnetization (Fig.3c,h) to a high degree (RMSE=0.035/0.015, SSIM=0.88/0.86). For centric and linear reordering different flip angle patterns are generated (Fig.3,d,i), which deviate strongly from a 180° refocusing flip angle train. In vivo measurements of the final sequences with and without DenseNet processing are shown in Figure 4 and compared to a conventional 180° flip angle train and reconstruction, showing that the approach generalizes to measured in vivo data and removes blurring accordingly. Combining optimal sequence and tailored CNN yields the best deblurring performance.

Discussion

For centric reordering in both, simulation and in vivo, measurements show a major improvement of blurring in phase encoding direction. In the in vivo measurement, grey and white matter contrast is enhanced compared to the reference image and the structures around the skull are clearly better resolved. For linear reordering, the simulation shows good agreement to the target transverse magnetization, however, the reference TSE sequence does not exhibit a lot of blurring or Gibbs ringing to start with. This is mostly due to already strongly decayed signal intensity in white and grey matter, which is caused by the long echo train for a single-shot TSE. In the in vivo measurement, a slight increase in sharpness of the image can be observed, but also an amplification of noise, which is typical for deblurring operations. A sophisticated noise model during simulation or denoising algorithms could provide further improvements.
The flip angle design (Fig.5) for linear reordering resembles TRAPS Pulses[1, Fig.3]. The design for centric reodering shows similarity to flip angle pattern in [7, Fig.1]. However, in both cases distinguished differences in the flip angle patterns are observed, which can be explained by the combination of flip angle design and CNN post-processing. This hints to a new optimal sequence design in general, where trained NN reco or evaluation is included during the optimization.

Conclusion

We demonstrated the removal of T2-induced blurring in single-shot TSE sequences by a joint optimization of flip angle design and DenseNet parameters, generating a pseudo-inverse of the PSF perturbed FFT, which is able to obtain the original transverse magnetization image at a certain TE. This approach can be extended for other transient sequences with complex voxel-T1/T2-dependent PSF.

Acknowledgements

No acknowledgement found.