Introduction

MR fingerprinting (MRF) enables robust simultaneous quantitative multiparametric mapping in a single acquisition (1,2). The feasibility of combining T1 and T2 maps with apparent diffusion coefficient (ADC) maps for improving diagnosis of prostate cancer has been demonstrated (3,4). However, image quality of the T1 and T2 maps was suboptimal, which was due to geometric distortions in the prostate regions resulting from the long spiral acquisition readout. This work proposes to use radial sampling to minimize the effects of B0 inhomogeneity and temporal subspace reconstruction to accelerate the acquisition for fast distortionless T1 and T2 mapping in the prostate in less than 4 minutes. The proposed subspace radial MRF was tested on a volunteer & a patient with prostate cancer.

Methods

Radial MRF data acquisition
A multi-slice gradient-spoiled steady-state-free-precession (SSFP) MRF sequence with inversion preparation was used with golden angle radial trajectory readout (5) on a 3T Philips Elition (Philips, Best, The Netherlands). MRF acquisition parameters are as follows: FOV = 250 x 250 mm2, image matrix = 224 x 224, slice thickness = 5 mm, number of slices = 15, echo time (TE) = 4 ms, repetition time (TR) = 10 ms, variable flip angle range = 0-60 degrees. The utilized acquisition schedule contains 500 time points. One prostate patient and one healthy volunteer subject were recruited and gave informed consent in accordance with institutional IRB. Acquisitions with 3 and 5 radial spokes per time point were performed to cover the entire prostate, with scan times of 3:47min and 6:18min, respectively. The prostate, peripheral and transitional zones and visible dominant lesion (patient) were delineated for each study, and the statistics and distribution of the quantitative mapping values were analyzed.
Subspace MRF reconstruction:
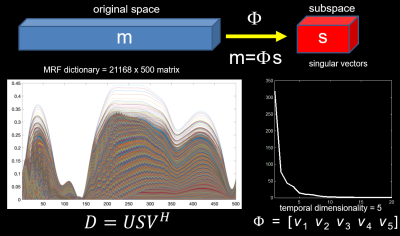
Since the entries of the MRF dictionary present extensive correlations, a temporal subspace can be estimated to constrain the reconstruction of the time-series of undersampled frames (Figure 1). Given the subspace defined by Φ, the high-dimensional time-series m (500 dynamics) can be projected into the subspace s= Φm. Since s will have a lower dimensionality, it will require fewer k-space samples per time point. In this work, the subspace was defined using the first 5 right singular vectors of the MRF dictionary, which represents a 100-fold dimensionality reduction. Subspace MRF reconstruction is performed by solving the following optimization problem:
$$ \mathop\arg\min_{s}\frac{1}{2}\parallel E\phi s-d\parallel _2^2 + \lambda \parallel Ts \parallel_{1} $$
where E represents the mapping from k-space (kx, ky, t, ch) to (x,y,t), = k-time raw data, m = space-time data, and T is transform to promote sparsity in s. The reconstruction was implemented in Matlab using a non-linear conjugate gradient algorithm.
To evaluate the image quality improvements resulting from subspace MRF reconstruction, standard nonuniform Fourier transform (NUFFT) reconstruction, and a golden-angle radial sparse parallel (GRASP) reconstruction method (6) were also performed, and resultant T1 and T2 parameter maps were compared. T1, and T2 relaxation parameter maps were calculated by dot product matching to the simulated MRF dictionary.

Results

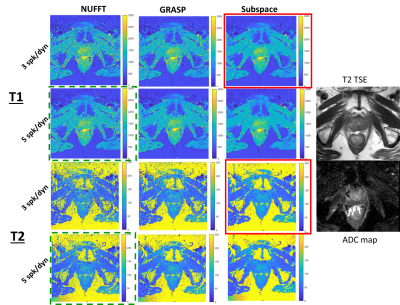
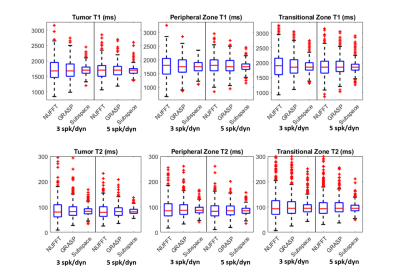
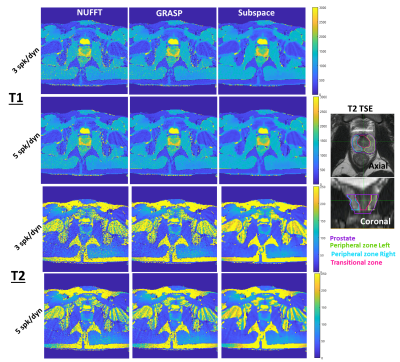
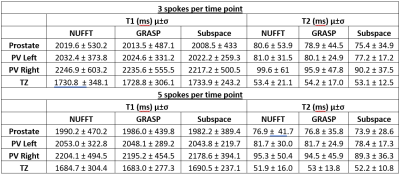
Figure 2 shows the resulting quantitative T1 and T2 maps from 3 and 5 spoke/dynamic acquisitions with NUFFT, GRASP, and the proposed subspace reconstructions. The lesion is indicated with white arrows on the clinical apparent diffusion coefficient map. The proposed subspace reconstruction on the 3 spoke/dynamic acquisition, indicated within red boxes, resulted in image quality significantly superior to that of 5 spoke/dynamic acquisition with standard NUFFT reconstruction, indicated by green dashed boxes. Subtle but visible difference in T1 and T2 values in the tumor region can be visualized in the subspace MRF parameter maps. This result indicates that significant reduction in acquisition time while still maintaining image quality with the proposed method is feasible. Figure 3 demonstrates trends of the delineated tumor region, peripheral zone, and transitional zone with different reconstruction methods. For all evaluated regions and both T1 and T2 parameter maps, noticeable decrease in spread of the T1 and T2 values can be observed, with the proposed subspace MRF having the least spread in values. Figure 4 demonstrates the parameter maps in a healthy volunteer for all acquisitions & reconstruction methods, as well as delineated regions for analysis. Excellent image quality was achieved with subspace MRF reconstruction, and 3 spoke/dynamic acquisition appears to be qualitatively comparable with the 5 spoke/dynamic subspace MRF image maps. Table 1 shows the mean & standard deviation values of all evaluated regions-of-interest in the healthy volunteer dataset. The reduction in standard deviation with the proposed method without bias to mean T1 and T2 value is also demonstrated. The T1 and T2 values are in agreement with values reported in literature (3,4). With subspace MRF, results from both long & short acquisitions are nearly identical, indicating that 3 spoke/dynamic acquisition could be the superior option under ideal acquisition conditions.

Discussion/Conclusion

This work demonstrated the feasibility of fast distortionless T1 and T2 mapping using golden-angle radial MR fingerprinting and a novel subspace dynamic reconstruction technique. This approach not only significantly improves image quality compared with standard reconstruction methods, but also enables substantial shortening of scan time without sacrificing image quality and quantitative mapping accuracy. In future work, quantitative mapping repeatability as well as patient-specific image quality variations will be further examined.

Acknowledgements

This research work was performed in collaboration and under an institutional master research agreement with Philips Healthcare. This work was partially supported by the NIH/NCI Cancer Center Support Grant/Core Grant (P30 CA008748). The authors would like to thank the MRI technologists and therapists in the MSKCC Department of Radiation Oncology for their skilled assistance.