2555
On the complexity of pTx systems in SAR assessment
Johannes Petzold1, Bernd Ittermann1, and Frank Seifert1
1Physikalisch-Technische Bundesanstalt (PTB), Berlin, Germany
1Physikalisch-Technische Bundesanstalt (PTB), Berlin, Germany
Synopsis
Different methods for SAR control (SAR limit, phase-agnostic SAR limit, amplitude limit) are evaluated in a simulation study of parallel transmit (pTx) body coil systems (2,4, or 8 channels) at different B0 (0.5T, 1.5T, 3T). Criteria are the necessary safety factors to accommodate for subject variability, and the resulting mean(B1+). Due to the high safety factor necessary for a phase-based SAR limit, its mean(B1+) performance becomes effectively the same as the much simpler to implement amplitude limit.
Introduction
To assess patient safety for parallel transmission (pTx) setups, commonly Q-matrices1 for local-SAR calculations are determined by extended electromagnetic simulations and then compressed to virtual observation points (VOPs)2. VOP Q-matrices from different ‘anchor simulations’ (one specific human voxel model, in our case) can be combined to derive overarching SAR limits. Still, additional safety factors must be applied to extrapolate from the investigated anchors to all conceivable patients. Adding more anchors and therefore more Q-matrices results in stricter safety limits and degraded$$$\,B_1^+$$$ performance. However, the safety factor for extrapolation to non-anchor models is also expected to shrink3.In this simulation study, three SAR control modes are compared in terms of safety and mean($$$B_1^+$$$) performance. Field strengths$$$\,B_0\leq3T$$$ are investigated, where pTx gains renewed interest as a mean to mitigate implant hazards4–7.
Methods
Field data generationTen human voxel models (nine from the virtual population8 plus XCAT9, see Tab.1 were simulated in a 48-port pTx body coil3 at 0.5T, 1.5T and 3.0T with their hearts in the central plane using Sim4Life10. Combining elements accordingly, pTx coils with 8 loops, 4 loops and 2 linearly polarized channels were subsequently obtained by co-simulations11.
Six voxel models from 50–80kg and without obvious artifacts were used for anchor-model analysis. For all combinations of channel count and$$$\,B_0$$$, 10g-averaged Q-matrices as well as whole body- and head-Q-matrix were computed and divided by their respective IEC limits12. These normalized Q-matrices were then compressed to VOPs$$$\,\hat{Q}^{(k)}$$$ with 10% overestimation13.
Safety limits
A complex excitation vector $$$u$$$ is safe, if one of the following conditions is fulfilled for each VOP $$$k$$$:
SAR limit (SL):$$u^\dagger\,\hat{Q}^{(k)}u\leq\,1$$
phase agnostic SAR limit (PASL):$$|u|\,|\hat{Q}^{(k)}|\,|u|\leq\,1$$
amplitude limit (AL):$$\max_{ch}|u_{ch}|\leq\alpha$$
where $$$|\,\cdot\,|$$$ denotes the element-wise absolute value, and $$$\alpha$$$ is the maximum single-channel amplitude $$$\alpha\equiv\min_k[(\sum_{ij}|Q_{ij}^{(k)}|)^{-1/2}]$$$14.
Safety factor
Out of the six remaining voxel models,$$$\,p$$$ were selected as anchors ($$$1\leq\,p\,\leq5$$$) and a different one as the target. 10000 random excitation vectors (half with random amplitudes and phases, half with equal amplitudes and random phases) were scaled such that the respective safety limit is approached for a given set of anchor simulations. These vectors are used to calculate the normalized peak spatial SAR (psSAR) of the selected target simulation. This is done for all 186 combinations of one target and$$$\,p$$$ anchor simulations. Mean($$$B_1^+$$$) was assessed with an overall safety limit consisting of all VOPs multiplied with the maximum normalized psSAR of$$$\,p=5$$$.
Results
In Fig.1 the maximum safe single-channel amplitude$$$,\alpha$$$ is plotted vs. body mass. Except for 2Tx at 3T, differences between comparable masses tend to be <30%. For 0.5T and 1.5T, a higher mass tends to result in a lower safe amplitude. For 3T, such trend is less obvious. No clear field dependence exists.Anchor-safe excitations can still create unsafe psSAR in the unknown target model, with highest values under SL control and lowest for AL (Fig.2). IEC limits can be exceeded up to 3.4 times and this overshoot depends mainly on the channel count but not on $$$\,B_0$$$. For SL, psSAR overshoot and hence the safety factor clearly increases with channel count, for PASL and AL they tend to decrease. With higher anchor model count, the maximum normalized psSAR in the target simulation drops (Fig.3). Taking the respective safety factors into account, a higher channel count can result in a lower mean($$$B_1^+$$$) performance (Fig.4).
Discussion
Reconsidering pTx for$$$\,B_0\leq3T$$$ is driven by the anticipation to mitigate implant heating if multiple Tx channels are available5. The concept must also work without implants, however, and for the prevalent local SAR control there seems to be an optimal channel count in terms of $$$B_1^+$$$ performance. For higher channel counts, PASL and AL become very conservative before applying the safety factor, while SL is punished by the safety factor.In the investigated implant-free case, a 2-channel system with SL provides the best mean $$$B_1^+$$$ performance. Once implants in various conceivable configurations are added, higher channel counts might be needed for best mitigation and $$$B_1^+$$$ performance. Here, the AL appears advantageous due to its robustness and simplicity. The model dependance is low (<30% except for 3T, 2ch) and SAR supervision much simpler as only amplitudes (or power levels) need to be checked. In addition, AL has the nice feature that an upper bound for psSAR can be calculated. For 0.5T and 1.5T, such amplitude limit might even be derived just from the patient’s mass. For 3T, the picture is less clear. For SL, any extrapolation too far beyond the investigated anchor simulations appears to be critical. Anchor models close to the given patient are presumably needed for good $$$B_1^+$$$ performance as using the VOPs of an 120kg adult would result in a bad performance for a 30kg child.
Conclusion
A framework to systematically evaluate pTx systems in terms of RF safety and B1 performance was developed and applied to chest imaging at$$$\,B_0=0.5T,\,1.5T\,$$$and $$$3T$$$. For all $$$\,B_0$$$, inter-subject variation of the ubiquitously applied local SAR limits increases substantially with pTx channel count. After applying the necessary safety factors, the more robust and easily to implement RF-amplitude monitoring achieves an identical performance for an 8Tx system at 3T.Acknowledgements
This work has received funding from the EMPIR programme co-financed by the Participating States and from the European Union's Horizon 2020 research and innovation programme, under grant number 17IND01 – MIMAS.References
- Bardati F, Borrani A, Gerardino A, Lovisolo GA. SAR optimization in a phased array radiofrequency hyperthermia system. IEEE Trans. Biomed. Eng. 1995;42:1201–1207 doi: 10.1109/10.476127.
- Eichfelder G, Gebhardt M. Local specific absorption rate control for parallel transmission by virtual observation points. Magn. Reson. Med. 2011;66:1468–1476 doi: 10.1002/mrm.22927.
- Petzold J, Ittermann B, Seifert F. Robustness of pTx safety concepts to varying subjects and subject positions. In: Proc. Intl. Soc. Mag. Reson. Med. 29. ; 2021. p. 116.
- Silemek B, Seifert F, Petzold J, et al. Rapid safety assessment and mitigation of radiofrequency induced implant heating using small root mean square sensors and the sensor matrix Q s . Magn. Reson. Med. 2021:mrm.28968 doi: 10.1002/mrm.28968.
- Winter L, Seifert F, Zilberti L, Murbach M, Ittermann B. MRI‐Related Heating of Implants and Devices: A Review. J. Magn. Reson. Imaging 2020:jmri.27194 doi: 10.1002/jmri.27194.
- Eryaman Y, Guerin B, Akgun C, et al. Parallel transmit pulse design for patients with deep brain stimulation implants. Magn. Reson. Med. 2015;73:1896–1903 doi: 10.1002/mrm.25324.
- McElcheran CE, Yang B, Anderson KJT, Golenstani-Rad L, Graham SJ. Investigation of Parallel Radiofrequency Transmission for the Reduction of Heating in Long Conductive Leads in 3 Tesla Magnetic Resonance Imaging Xu B, editor. PLOS ONE 2015;10:e0134379 doi: 10.1371/journal.pone.0134379.
- Gosselin M-C, Neufeld E, Moser H, et al. Development of a new generation of high-resolution anatomical models for medical device evaluation: the Virtual Population 3.0. Phys. Med. Biol. 2014;59:5287–5303 doi: 10.1088/0031-9155/59/18/5287.
- Segars WP, Sturgeon G, Mendonca S, Grimes J, Tsui BMW. 4D XCAT phantom for multimodality imaging research: 4D XCAT phantom for multimodality imaging research. Med. Phys. 2010;37:4902–4915 doi: 10.1118/1.3480985.
- Sim4Life 6.0, ZMT Zurich MedTech, Zürich, Switzerland
- Kozlov M, Turner R. Fast MRI coil analysis based on 3-D electromagnetic and RF circuit co-simulation. J. Magn. Reson. 2009;200:147–152 doi: 10.1016/j.jmr.2009.06.005.
- IEC 60601-2-33: Medical electrical equipment – Part 2-33: Particular requirements for the basic safety and essential performance of magnetic resonance equipment for medical diagnosis. International Electrotechnical Commission; 2015.
- Orzada S, Fiedler TM, Quick HH, Ladd ME. Local SAR compression algorithm with improved compression, speed, and flexibility. Magn. Reson. Med. 2021;86:561–568 doi: 10.1002/mrm.28739.
- Seifert F, Cassara A, Weidemann G, Ittermann B. Reliable and robust RF safety assessment of transmit array coils at ultrahigh fields. In: Proc. Intl. Soc. Mag. Reson. Med. 22. ; 2014. p. 4891.
Figures
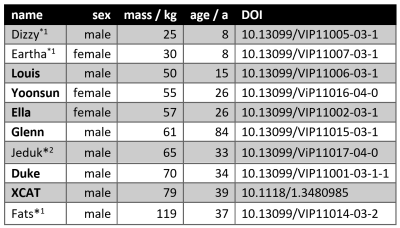
Table 1. Voxel
models included in analysis with their mass and DOI. *1Excluded due
to mass not in interval (50kg,80kg). *2Excluded due to hot spot
between right arm and torso.
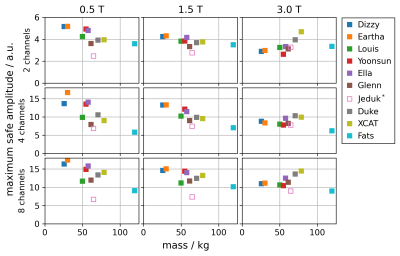
Figure 1.
Maximum safe amplitude as a function of mass for all virtual human voxel
models. Maximum safe amplitude is only row-wise comparable. *Model Jeduk
shows a hotspot between right arm and torso as artefact.
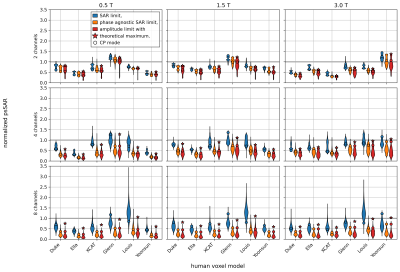
Figure 2.
Violin
plots showing the distribution of the normalized psSAR of one voxel model for all
10000 tested excitation vectors that were scaled to satisfy all safety limits
derived from the remaining 5 voxel models. The CP mode is separately marked
with a circle. The theoretical maximum for the amplitude limit for the given
models is marked with a star.
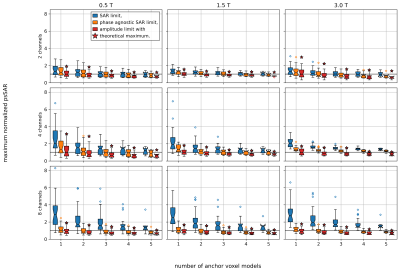
Figure 3. Normalized psSAR was calculated for all possible combinations of anchor models
and target model and grouped by their number of anchor models p. Boxplots of maximum
normalized psSAR of each combination.
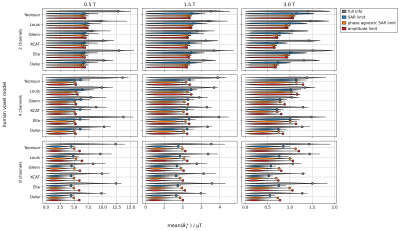
Figure 4. Mean(B1+)
performance of all voxel models. Full info assumes full knowledge of the
patient ignoring model uncertainties. Then, SAR is limited by the VOPs of the
respective patient model only without taking into account a safety factor. All
other safety limits use the VOPs of all 6 models with a safety-factor derived
from the highest possible SAR when using 5 anchor simulations.
DOI: https://doi.org/10.58530/2022/2555