2550
New “restricted SAR mode” definition based on a thermal conservative model for relaxed unconditional safe in vivo experiments
Natalia Dudysheva1,2, Nicolas Boulant1, Alexandre Vignaud1, and Franck Mauconduit1
1CEA, NeuroSpin, Paris-Saclay University, CNRS, Gif-sur-Yvette, France, 2Multiwave Imaging, Marseille, France
1CEA, NeuroSpin, Paris-Saclay University, CNRS, Gif-sur-Yvette, France, 2Multiwave Imaging, Marseille, France
Synopsis
In this work, we propose to extend the capacities of ultra-low SAR protocol used in coil design. A developed restricted SAR protocol holds the worst-case SAR below the threshold by constraining the total transmitted RF power. Since SAR reflects tissue heating, we exploit a conservative thermal model to derive relaxed SAR constraints depending on acquisition time. This enables to extend the options available for sequences played under this mode, including fat suppression, higher image resolution, or decreased TR.
Introduction
Standard MRI examinations impose specific absorption rate (SAR) limitations to ensure patient safety. For head studies, the IEC guidelines set the limits of 3.2 W/kg and 10 W/kg for the whole-head and local (10 grams of tissue) SARs for 6 min and double these values for 10 seconds1. These conditions should guarantee that temperature rise does not exceed 2 degrees under basal conditions of 37 °C. Specific MRI studies suggest a severe SAR limitation to safely study patients with implants2,3 or evaluate coil design in vivo4 without SAR pre-simulations. In this context, the restricted SAR methodology4 automatically respects SAR limits for all sequence settings and coils by assuming that the total transmitted power is entirely absorbed by a 10-gram tissue area. Thus, the maximum average power is 0.1 W for 6 min (0.2 W for 10 sec). This situation represents an overstated limitation but does not make any assumption about the SAR distribution. Here, we propose to estimate conservatively the temperature rise of this 10-gram sphere of tissue and examine the conditions to relieve the restrictions while preserving the safety aspects based on the maximum temperature rise limit.Methods
Assuming all the power absorbed by a sphere of 10g of tissue (R=1.34 cm considering the brain tissue density) and only heat conduction in an infinite continuous medium, the temperature rise over time induced by RF energy absorption obeys the following diffusion equation: $$ρC\frac{\partial T}{\partial t}-κ\Delta T=ρSAR.$$ Here ρ=1000 kg/m3 is the density, C=4000 J·kg-1·K-1 denotes the specific heat capacity, and κ=0.5 Wm-1·K-1 corresponds to the thermal conductivity. These values do not vary strongly with the head tissues. We first consider SAR as a source with a uniform distribution within the sphere. By introducing α=κ/(ρC), transforming the equation into Fourier space, solving several integrals, and going back to the spatial domain, the exact analytical result for the maximum temperature in the sphere center can be obtained: $$T_{max}(t)=\frac{ρSAR}{2κ}R^2 \left(1-\sqrt{\frac{4αt}{πR^2}}e^{-\frac{R^2}{4αt}} - \left(1-2\frac{αt}{R^2}\right)erf \left(\frac{R}{2\sqrt{αt}}\right) \right).$$ Next, we compare the result with the Gaussian distribution case, where $$$SAR(x,y,z)=be^{-\frac{x^2+y^2+z^2}{2σ^2}}.$$$ The same methodology provides the maximum temperature rise described by the following exact expression: $$T_{max}(t)=\frac{ρbσ^2}{κ}\left(1 - \frac{1}{\sqrt{1+\frac{2αt}{σ^2}}} \right) \quad with \quad b=\frac{10V}{4π}\left(σ^3\sqrt{\frac{π}{2}}erf\left(\frac{R}{σ\sqrt{2}}\right) - Rσ^2e^{-\frac{R^2}{2σ^2}}\right)^{-1},$$ where V is the sphere volume, and b corresponds to the normalization constant so that the average SAR over the 10g sphere is equal to a given value (here 10 W/kg). The parameter σ of the Gaussian distribution must be less than R/2 so that the analytical calculation is consistent with the assumption of all power absorbed by the sphere. Given these analytical results, the parameters (flip angles, pulse bandwidths, TR, TA, SAR levels) of the sequences (e.g. GRE, XFL, and EPI) can be safely adapted depending on the duration of the acquisition.Results
The temperature rise over time for different power levels with a uniform SAR distribution as well as the maximum exam time for a given SAR are reported in Fig. 1. Experiment duration of fewer than 50 minutes allows increasing previous power limits (0.1 W for 6 min and 0.2 W for 10 s) by 1.5; below 15 minutes, the augmentation ratio is 2. A comparison of uniform versus Gaussian SAR distributions is represented in Figure 2. More peaked SAR distributions define stricter SAR constraints.Discussion
We show that depending on the exam duration, the SAR thresholds based on the restricted SAR methodology can be relaxed. The temperature results, more relevant than SAR from a safety standpoint, strongly depend on the shape of the SAR distribution in the sphere where all RF power is supposed to be absorbed. However, the model makes extremely conservative assumptions, such as all RF power absorbed in the 10g area, no heat-dissipation mechanisms besides heat conduction, and no perfusion. As a result, considering a uniform SAR distribution appears a reasonable counterpart to relax the SAR constraints. Thus, such a drastic and simplistic model still allows scanning human subjects safely without prior SAR simulations using adapted restricted SAR protocols. Relaxing the constraints based on a temperature analysis permits up to twice the resolution or coverage, or additional fat suppression, which can be an essential feature, for example, in EPI imaging5,6.Conclusion
The considered analytical calculations provide the local heating dynamics for given input power, whether it is a single channel or parallel transmission. Neglect of perfusion makes the model conservative7. We show that reducing the acquisition time entails a lower final temperature and thus permits increased SAR limits. Relaxation of the SAR constraints enables higher image resolution, better coverage, shorter TR, etc., thereby expanding the restricted SAR methodology applications and increasing opportunities for low-power research.Acknowledgements
The study has received funding from the European Union Horizon 2020 Research and Innovation program under Grant Agreements No. 736937 (M-One) and No. 885876 (AROMA). Leducq Foundation (Large Equipement ERPT program, NEUROVASC7T project) also provided financial support for this work.References
- International Electrotechnical Commission Medical electrical equipment-part 2–33: particular requirements for the basic safety and essential performance of magnetic resonance equipment for medical diagnosis - 3rd ed. Geneva: International Electrotechnical Commission: 2010- 2–33:601.
- Subhendra N. S., Alterman R. L. et al. Low Power MRI Techniques for Neurosurgical Planning and Post-surgical Assessment of Deep Brain Stimulators in Patients with Medically Refractory Parkinson’s Disease or Dystonia. IOSR Journal of Dental and Medical Sciences, 2016; Volume 15(10) pp. 71-75.
- Wheaton A. J., Borthakur A. et al. Method for Reduced SAR T1ρ-Weighted MRI. Magnetic Resonance in Medicine, 2004; 51:1096–1102.
- Vignaud A, Mauconduit F. et al. Fast and unconditionally safe in vivo MR head protocol for home-made coil prototype assessment at 7T. Journal of Physics: Conference Series, IOP Publishing, 2018; 1092, pp.012159.
- Burakiewicz J, Charles-Edwards G. D., et al. Water–Fat Separation in Diffusion-Weighted EPI Using an IDEAL Approach with Image Navigator. Magnetic Resonance in Medicine, 2015; 73:964–972.
- Sarlls J. E., Pierpaoli C., et al. Robust Fat Suppression at 3T in High-Resolution Diffusion-Weighted Single-Shot Echo-Planar Imaging of Human Brain. Magn Reson Med, 2011 Dec; 66(6): 1658–1665.
- Le Ster C., Mauconduit F., Mirkes C., Vignaud A., Boulant N. Measuring radiofrequency field-induced temperature variations in brain MRI exams with motion compensated MR thermometry and field monitoring. Magn Reson Med, 2021 online.
Figures
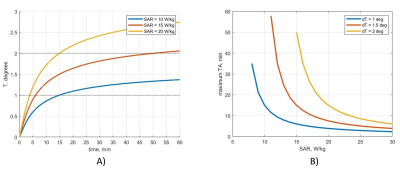
Fig. 1. A): Temperature rise for uniform power
distribution, B): maximum allowable exam duration depending on peak 10g SAR.
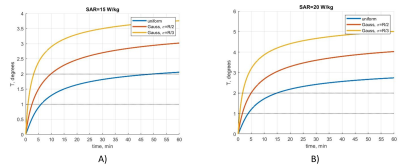
Fig. 2. Temperature rise for different peak SAR
values for A) SAR=15 W/kg and B) SAR=20 W/kg. The first SAR threshold (15 W/kg)
leads to a maximum acquisition time of 50 min for a uniform distribution and
9.8 min (𝜎 =R/2) and 3.1 min (𝜎=R/3) for Gaussian distributions
when the temperature rise limit is 2°C. For the peak SAR = 20 W/kg, the
duration thresholds are 15 min for a uniform distribution, 5 min (𝜎 =R/2) and 1.7 min (𝜎=R/3) for Gaussian distributions.
DOI: https://doi.org/10.58530/2022/2550