2530
Quantitative MRI parameter estimation with supervised deep learning: MLE-derived labels outperform groundtruth labels
Sean Epstein1, Timothy J.P. Bray2, Margaret A. Hall-Craggs2, and Hui Zhang1
1Centre for Medical Image Computing, University College London, London, United Kingdom, 2University College London, London, United Kingdom
1Centre for Medical Image Computing, University College London, London, United Kingdom, 2University College London, London, United Kingdom
Synopsis
We propose a novel deep learning technique for quantitative MRI parameter estimation. Our method is trained to map noisy qMRI signals to conventional best-fit parameter labels, which act as proxies for the groundtruth parameters we wish to estimate. We show that this training leads to more accurate predictions of groundtruth model parameters than traditional approaches which train on these groundtruths directly. Furthermore, we show that our proposed method is both conceptually and empirically equivalent to existing unsupervisedapproaches, with the advantage of being formulated as supervised training.
Introduction
Within the field of quantitative MRI (qMRI), there is widespread interest in the application of deep learning techniques to accelerate parameter estimation. To date, methods based on both supervised and unsupervised training have been applied to this problem1–3, with mixed results. Supervised methods have been shown to produce highly biased, but precise, estimates at low SNR4. In contrast, unsupervised methods produce more accurate parameter estimation at the cost of lower precision5. In this work, we propose a novel supervised approach that combines the advantages of traditional supervised and unsupervised approaches. We hypothesise that the benefits of unsupervised training can be incorporated into supervised approaches by explicitly encoding the mapping being implicitly learned by unsupervised methods. We propose that this can be achieved by training supervised networks on conventional best-fit parameter estimate labels rather than on groundtruth parameter values.Theory
Figure 1 compares our proposed method to two existing deep learning approaches. These methods take the same noisy signals as input but vary in the formulation of their loss functions. All three approaches aim to encode the mapping from noisy signals to groundtruth parameters, here referred to as the exact target function. Traditional supervised methods (SupervisedGT) do this directly, by explicitly minimising the distance between network output and groundtruth label:SupervisedGT:$$$L=\|W\cdot(Output-parameter_{GT})\|^2$$$, where W normalises inter-parameter magnitude differences and parameterGT are groundtruth parameter values
In contrast, our proposed method (SupervisedMLE) learns an approximate form of this function (the approximate target function) which maps noisy signals to their conventional best-fit parameters (maximum likelihood estimates (MLEs)). These MLE labels act as proxies for the groundtruth parameters we wish to estimate:
SupervisedMLE:$$$L=\|W\cdot(Output-parameter_{MLE})\|^2$$$, where parameterMLE are parameter estimates obtained from conventional maximum-likelihood fitting of input noisy signals.
Unsupervised methods implicitly learn this same approximate target function: outputs (parameters), converted to noise-free signal predictions by a qMRI model, are matched to inputs (noisy signals), just as in conventional MLE fitting:
Unsupervised:$$$L=\|M(Output)-input\|^2$$$, where M is the relevant qMRI signal model
By explicitly learning this approximate target function, our proposed method reformulates unsupervised parameter estimation as a supervised learning problem.
Methods
All three network types were trained on identical inputs, and their ability to reconstruct groundtruth qMRI parameters was compared on unseen datasets.Signal model
Two signal models were investigated, one non-linear (monoexponential) and one linear (straight line). Model 1 (monoexponential) was selected for (a) its relevance to qMRI (e.g. diffusion, relaxometry) and (b) its non-degeneracy (c.f. multiexponential models), simplifying the interpretation of network performance. Model 2 (straight line) was selected to remove model non-linearity as a potential explanation for our findings.
Model 1 (monoexponential): $$$S(x)=\theta_0e^{-x\cdot\theta_1}$$$
Model 2 (straight line): $$$S(x)=\theta_0-\theta_1\cdot x$$$
Data
Simulated datasets were generated at high and low SNRs by generating 100,000 noise-free signals from uniform parameter distributions ($$$\theta_0,\theta_1\in[0.8,1.2]$$$), sampling them ($$$x=[0,0,0,0,1,1,1,1]$$$), and adding noise. Rician noise was added to Model 1 to mimic MRI acquisitions; Gaussian noise was added to Model 2 to remove noise complexity as a potential explanation for our findings. In both cases, low SNR was defined as $$$\sigma=0.10$$$, and high SNR as $$$\sigma=0.05$$$, where $$$max(S_{noisefree})\in[0.8,1.2]$$$.
Network performance was tested on independently generated datasets with sampling, parameter distributions, and noise matching training.
Network architecture
Network architecture was harmonised across all experiments and represents common choices in the existing qMRI literature: 3 fully connected hidden layers, each with 8 nodes, and an output layer of 2 nodes representing the model parameter estimates. Wider networks were investigated and found to have equivalent performance at the cost of increased training time.
Results and discussion
Across all model and noise conditions, when testing against groundtruth model parameters, MLE-trained networks produced lower bias (Figures 2 & 4) and lower precision (Figures 3 & 5) than those trained on groundtruth labels; this divergence was most distinct at low SNR. Furthermore, MLE-trained networks produced comparable parameter estimation performance as unsupervised ones (Figures 2-5). Our results are consistent with recently reported findings that (a) groundtruth-based supervised training produces high bias, high precision estimates at low SNR4, and (b) unsupervised methods improve accuracy at the cost of lowered precision5.As discussed in §Theory, SupervisedGT networks attempt to learn the exact target function (Fexact), whereas both SupervisedMLE and Unsupervised networks learn the same approximation of it (Fapprox). The biased parameter estimates of SupervisedGT suggests that Fexact is difficult to learn directly; the improved performance offered by both SupervisedMLE and Unsupervised show that this target function may be more successfully learnt by explicitly targeting an approximation of it (Fapprox).
Our proposed method brings these benefits of unsupervised networks into a supervised framework by training on independently computed MLE labels. Compared to unsupervised methods, this has the advantage of (a) offloading MLE estimation to separate bespoke algorithms, (b) tailoring training performance to model parameters of interest, and (c) allowing the inclusion of additional information via training labels.
Conclusions
We propose a method which reduces the bias of supervised deep learning approaches to parameter estimation. Our method, which draws inspiration from the success of unsupervised methods, trains networks on noisy signals paired with independently-computed MLE parameter labels.Furthermore, this work sheds light on the relationship between supervised and unsupervised approaches to parameter estimation, and provides a conceptual link between these seemingly-distinct approaches.
Acknowledgements
This work is supported by the EPSRC-funded UCL Centre for Doctoral Training in Medical Imaging (EP/L016478/1). TJPB is supported by an NIHR Clinical Lectureship.References
- Barbieri S, Gurney‐Champion OJ, Klaassen R, Thoeny HC. Deep learning how to fit an intravoxel incoherent motion model to diffusion‐weighted MRI. Magn Reson Med. 2020;83: 312–321. doi:10.1002/mrm.27910
- Bertleff M, Domsch S, Weingärtner S, Zapp J, O’Brien K, Barth M, et al. Diffusion parameter mapping with the combined intravoxel incoherent motion and kurtosis model using artificial neural networks at 3 T. NMR Biomed. 2017;30: e3833. doi:10.1002/NBM.3833
- Golkov V, Dosovitskiy A, Sperl JI, Menzel MI, Czisch M, Sämann P, et al. q-Space Deep Learning: Twelve-Fold Shorter and Model-Free Diffusion MRI Scans. IEEE Trans Med Imaging. 2016;35: 1344–1351. doi:10.1109/TMI.2016.2551324
- Gyori NG, Palombo M, Clark CA, Zhang H, Alexander DC. Training data distribution significantly impacts the estimation of tissue microstructure with machine learning. Magn Reson Med. 2021;00: 1–16. doi:10.1002/MRM.29014
- Grussu F, Battiston M, Palombo M, Schneider T, Wheeler-Kingshott CAMG, Alexander DC. Deep Learning Model Fitting for Diffusion-Relaxometry: A Comparative Study. Math Vis. 2021; 159–172. doi:10.1007/978-3-030-73018-5_13
Figures
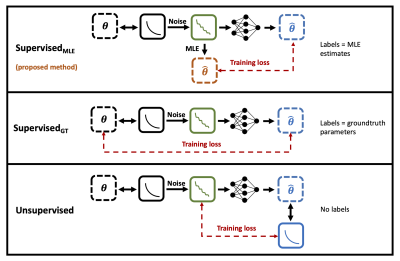
Comparison of our proposed training method (SupervisedMLE) with traditional supervised (SupervisedGT) and unsupervised approaches. In all cases, noise-free signals (black) are corrupted with noise (green) and fed as input into the networks. Dashed arrows (red) represent training loss: either between network output and independently-computed MLE estimates (SupervisedMLE); between network output and groundtruth parameters (SupervisedGT), or between a noise-free representation of network output and noisy input (unsupervised).
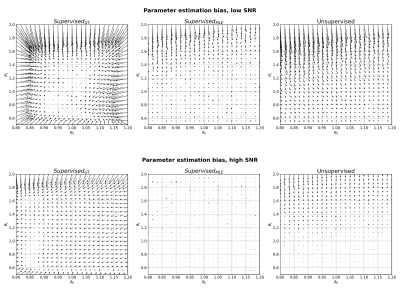
Parameter estimation bias for Model 1 (monoexponential) at low SNR (top) and high SNR (bottom). Arrows point from groundtruth parameter values to mean parameter estimates, averaged over 1000 noise instantiations.
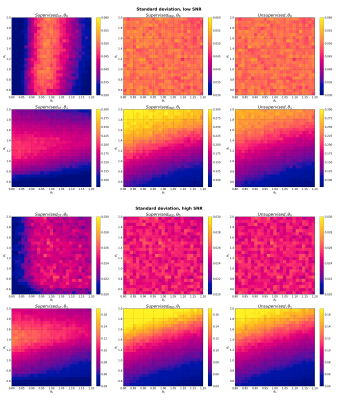
Parameter estimation standard deviation for Model 1 (monoexponential) at low SNR (top) and high SNR (bottom). Each panel shows the mean standard deviation of a given model parameter, at each point in two-dimensional parameter space, averaged over 1000 noise instantiations.
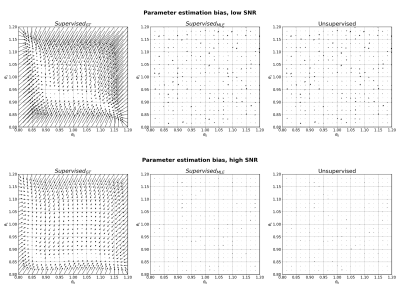
Parameter estimation bias for Model 2 (straight line) at low SNR (top) and high SNR (bottom). Arrows point from groundtruth parameter values to mean parameter estimates, averaged over 1000 noise instantiations.
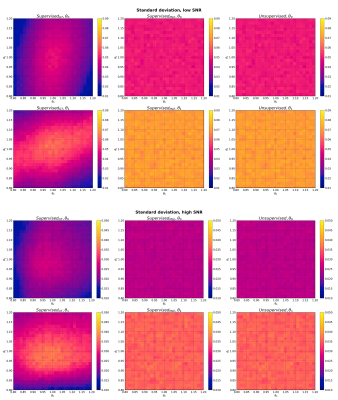
Parameter estimation standard deviation for Model 2 (straight line) at low SNR (top) and high SNR (bottom). Each panel shows the mean standard deviation of a given model parameter, at each point in two-dimensional parameter space, averaged over 1000 noise instantiations.
DOI: https://doi.org/10.58530/2022/2530