2528
Revised-NODDI with conventional dMRI data enabled by deep learning1Computer Science & Centre for Medical Image Computing, University College London, London, United Kingdom, 2AINOSTICS, Manchester, United Kingdom
Synopsis
This work shows that deep learning (DL) enables revised-NODDI parameter estimation from conventional dMRI data. Revised-NODDI is a recently proposed model which overcomes some limitations of NODDI. With conventional fitting methods, revised-NODDI parameters can be robustly estimated only in the presence of data acquired with multiple tensor-valued diffusion encodings. However, this new generation of acquisitions is not yet routinely available in clinical research. We show that revised-NODDI parameters estimated using conventional dMRI data via a DL framework are comparable with the parameters estimated fitting the model to data acquired using multiple tensor-valued diffusion encoding.
Introduction
This work assesses the feasibility of using deep learning (DL) to estimate revised-NODDI parameter maps from conventional diffusion MRI (dMRI) data alone. Revised-NODDI is a recently introduced version of NODDI model1,2, which has been shown to overcome some of the limitations of the original model3.Revised-NODDI is compatible with the new generation of dMRI data acquired with the so-called tensor-valued diffusion encoding (TVDE)4,5. A combination of TVDE acquisitions allows the direct estimation of the intra-neurite diffusivity2,3,6, which is fixed to a default value in the original version.
As an emerging technology, TVDE is not commonly available in clinical research. On the other hand, conventional dMRI data alone can not be used for a robust estimation of all the model parameters using traditional fitting methods7.
A possible solution is to fix the diffusivity value as done in the original model. However, in the presence of natural variation of the diffusivity, this approach would likely lead to a biased estimation of the other parameters.
DL has demonstrated capacity to reduce the imaging protocol requirements8,9. The question we try to answer in this work is whether DL can be used to bypass the requirement of TVDE acquisitions, enabling revised-NODDI parameter estimation using conventional dMRI data alone. Also, we assess how this compare with fitting revised-NODDI model on conventional dMRI data using a fixed value of intra-neurite diffusivity.
Materials and Methods
The experimental design is summarized in figure 1. We design a deep neural network (DNN) which takes conventional dMRI data as input and outputs revised-NODDI parameter estimations. We train the network on synthetic data and test it on in-vivo data.We compare the DNN estimated parameters with those obtained by fitting the model to data acquired with multiple TVDEs. The output maps will serve as ground truth (GT). Furthermore, we compare DNN estimation bias with the bias resulting from fitting a simplified version of revised-NODDI to conventional dMRI data alone.
In-vivo data
We use the dataset publicly available at https://github.com/filip-szczepankiewicz/Szczepankiewicz_DIB_201910. In brief, the dataset comprises one subject acquired with multiple TVDEs. In this work we use data acquired with linear tensor encoding (LTE), corresponding to the conventional dMRI acquisitions, and with spherical tensor encoding (STE).
Conventional Model fitting
We fit revised-NODDI model to LTE and STE in-vivo data jointly. We fit a simplified version of revised-NODDI to LTE in-vivo data alone. This simplified version fixes the isotropic intra-neurite diffusivity (dI) to 0.76 μm2/ms(2).
DNN architecture
The input of the network is the direction-averaged signal; the outputs are the model parameters. Specifically, we focus on predicting the neurite density index (NDI), the free-water fraction (FWF) and dI. The network comprises three hidden layers with 150 nodes each and ReLU8. A mean squared error loss is used between the network predictions and the parameters used to generate the synthetic signal. The DNN is trained in 200 epochs with a batch size of 250, a learning rate of 0.001 and Adam optimizer.
Synthetic data
We use the LTE in-vivo data protocol to generate synthetic signal from N=104 combinations of model parameters via revised-NODDI forward model. The parameters are sampled from ad-hoc random distributions. We add Rician noise to each measurement such that SNR(b=0)=30. We direction-average the signal to forgo directional dependence of the signal.
Results and discussions
Figure 2 shows that DNN using LTE data can predict revised-NODDI maps (left column) which are similar to the GT (right column). NDI map looks noisier than GT, but no systematic bias can be observed in the difference map (central column). FWF and dI difference maps reveal a systematic bias in the posterior white matter (WM) tracts. This bias is likely to be caused by the incapacity of DNN to capture the larger deviation of dI parameter in that region compared to the mean.Top panel of figure 3 shows that the mean of the difference between DNN parameter estimation and GT is close to zero both in in grey matter (GM) and WM, especially for NDI and FWF. Bottom panel of the figure confirms that the estimation bias of all the parameters is mainly driven by dI GT values.
Figure 4 shows that the maps obtained fitting the simplified revised-NODDI model to LTE data are similar to the GT. Compared to DNN output, the maps look almost identical. However, the difference maps reveal more systematic biases, especially for NDI and FWF parameters.
Figure 5 confirms quantitatively that NDI and FWF estimation from LTE fit suffer from a higher estimation bias compared to the DNN approach. The only exception is the FWF estimated in WM, whose bias is comparable to DNN’s.
Conclusions
We show that DL can be used to estimate revised-NODDI parameters from conventional dMRI in-vivo data. This result may facilitate the translation of revised-NODDI into clinical practice. We show that our DL-based approach outperforms, in terms of estimation bias, the conventional fitting method on LTE data, using a fixed value of diffusivity.DL predictions could be further improved via a fine tuning of both the training label distributions and the network. The behaviour of the network with atypical parameter values (such as in pathological tissues) should be further assessed.
Acknowledgements
No acknowledgement found.References
1. Zhang, H., et al., NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. Neuroimage, 2012. 61(4): p. 1000-16.
2. Guerreri, M., et al., Revised NODDI model for diffusion MRI data with multiple b-tensor encodings, in International Society for Magnetic Resonance in Medicine. 2018: Paris, France.
3. Guerreri, M., et al., Tortuosity assumption not the cause of NODDI’s incompatibility with tensor-valued diffusion encoding, in International Society for Magnetic Resonance in Medicine. 2020: Virtual conference.
4. Westin, C.F., et al., Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage, 2016. 135: p. 345-62.
5. Topgaard, D., Multidimensional diffusion MRI. J Magn Reson, 2017. 275: p. 98-113.
6. Lampinen, B., et al., Neurite density imaging versus imaging of microscopic anisotropy in diffusion MRI: A model comparison using spherical tensor encoding. Neuroimage, 2017. 147: p. 517-531.
7. Jelescu, I.O., et al., Degeneracy in model parameter estimation for multi-compartmental diffusion in neuronal tissue. NMR Biomed, 2016. 29(1): p. 33-47.
8. Golkov, V., et al., q-Space Deep Learning: Twelve-Fold Shorter and Model-Free Diffusion MRI Scans. IEEE Trans Med Imaging, 2016. 35(5): p. 1344-1351.
9. de Almeida Martins, J.P., et al., Neural networks for parameter estimation in microstructural MRI: Application to a diffusion-relaxation model of white matter. Neuroimage, 2021. 244: p. 118601.
10. Szczepankiewicz, F., S. Hoge, and C.F. Westin, Linear, planar and spherical tensor-valued diffusion MRI data by free waveform encoding in healthy brain, water, oil and liquid crystals. Data Brief, 2019. 25: p. 104208.
Figures
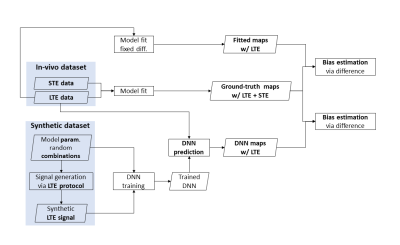
Fig 1: schematic view of the experimental design. The ground truth is obtained fitting revised-NODDI model to spherical tensor encoding (STE) and linear tensor encoding (LTE) in-vivo data. The DNN is trained using LTE synthetic data. Model parameter predictions are obtained from unseen LTE in-vivo data. Parameter estimations are also obtained fitting revised-NODDI with a fixed value of intra-neurite diffusivity to LTE data. Bias of the estimations are obtained computing the difference between the parameters and their ground truth.
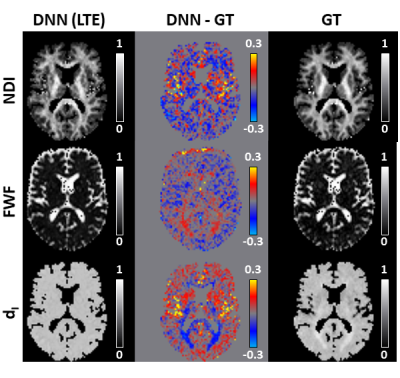
Fig 2: revised-NODDI maps via deep neural network (DNN) vs ground truth (GT) from in-vivo data. We compare one representative slice of neurite density index (NDI), free water fraction (FWF) and intra-neurite isotropic diffusivity (dI) parametric maps predicted by the DNN using LTE data (left column) with the GT (right column). GT here is represented by the maps obtained fitting the revised-NODDI model to LTE and STE data jointly. The middle column shows the DNN-GT difference maps.
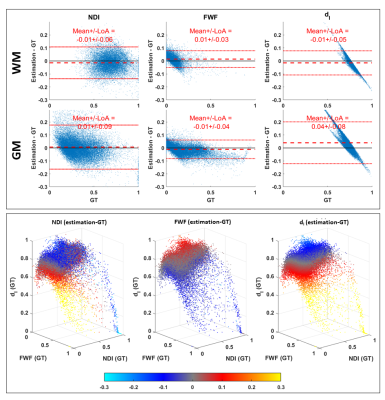
Fig 3: estimation bias of revised-NODDI parameters predicted by the DNN from in-vivo LTE data. Top panel shows Bland-Altman plots of NDI, FWF and dI. The plots are shown separately for white matter (WM) and grey matter (GM). Red dashed line indicates the mean value of the difference between the estimated parameter values and their ground truth. The red dotted lines indicate 95% limits of agreement (LoA). Bottom panel shows each parameter estimation bias reported as a function of the three GT parameter values. The bias is colour-coded using the same colourmap as the difference maps in fig. 2.
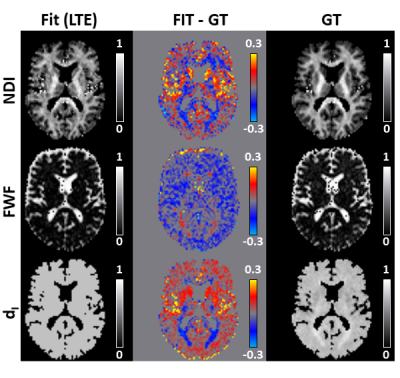
Fig 4: Same as figure 2 but comparing the output of fitting revised-NODDI model, with a fixed intra-neurite diffusivity value, to LTE data and the ground truth (GT) maps.
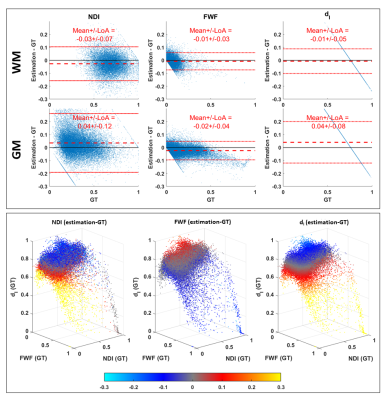
Fig 5: Same as figure 3 but reporting the estimation bias of fitting revised-NODDI model with fixed intra-neurite diffusivity to LTE data.